A man of mass m having a bag ofmas m slips from the roof of atall building of height H and starts falling vertically figure. When at a height h from the ground, he notices that the ground below him is pretty hard but there is a pond at a horizontal distnce x from the line of fall. In order to save himself he throws the bag horizontally (with respect to himself) in the direction opposite to the pond. Calculate the minimum horizontal velocity imparted to the bag so that the man lands in the water. If the man just suceeds toavoid the hard ground, where will the bag land?

Mass of man =M,
Initial velocity =O Mass of bag = m
Let the man throws the bag towards left with a velocity v.
So there is no exterN/Al force in the horizontal direction
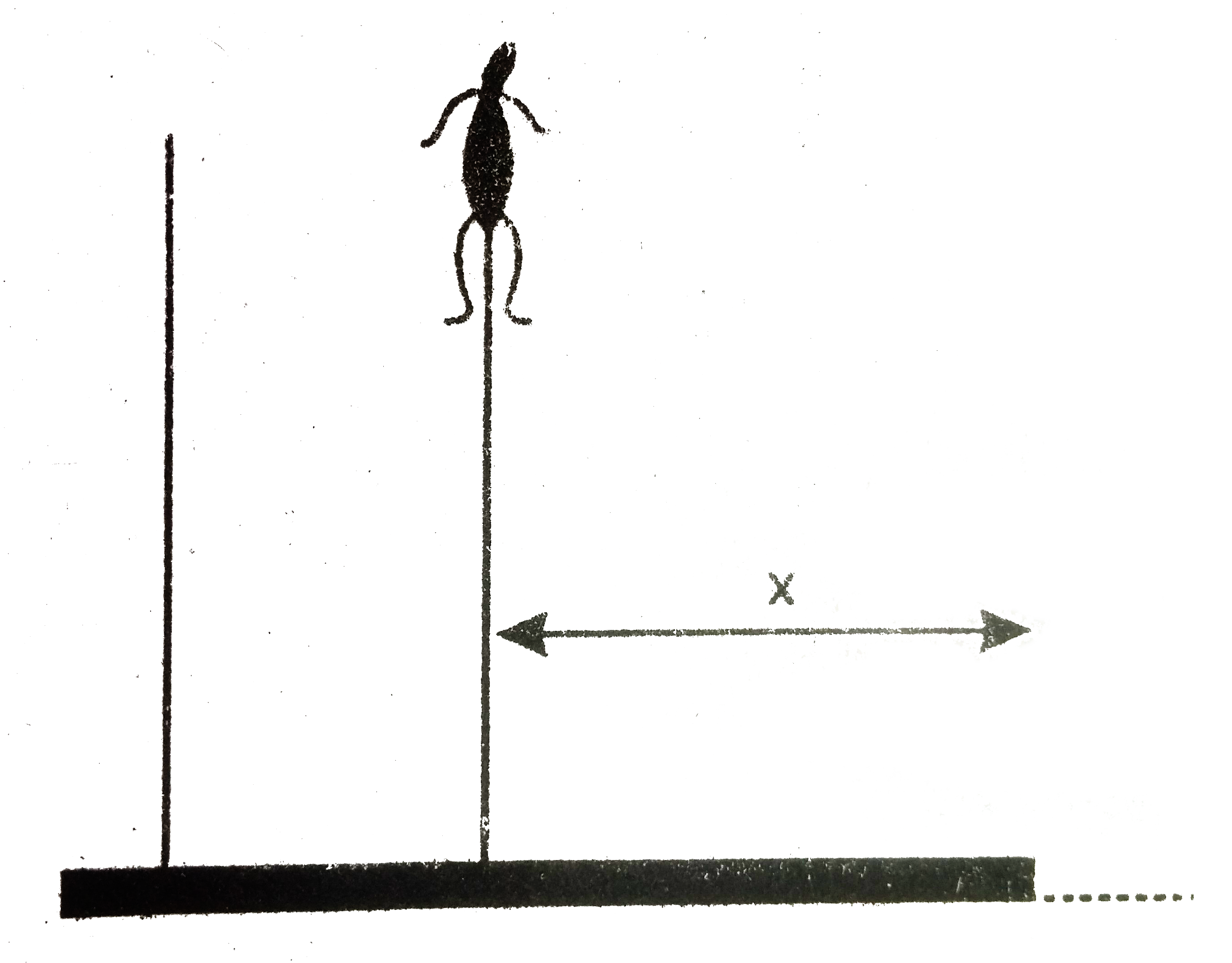
The momentum will be conserved.
Let the goes right with a velocity
mv=MV
rarr V=((mv)/M)<br>rarr v=((MV)/m)............i<br>Letthe→taltimehewilltake→reachgrond<br>=sqrt((2H)/g)=t_1<br>Letthe→taltimehewilltake→reachtheheighth<br>=t_2=sqrt((2(H-h))/g)<br>Thenthetimeofhisfly∈g<br>=t_1-t_2<br>=((2h)/g-)sqrt((2(H-h))/g)<br>=sqrt(2/g)(sqrtH-sqrt(H-h)<br>with∈thistimehereachestheground∈thepondcover∈gahorizontaldistance<br>rarr x=Vxxt <br>rarr V=x/t<br>v=M/m x/t<br>=M/mxxxx sqrtg/(sqrt(2)(sqrtH-sqrt(H-h))x<br>AsthereisnoexterNAlforce∈horizontaldirectionthex−corrdiNAteofCMwillrema∈attˆposition.<br>rarr 0=(Mxx(x)+mxxx_1)/(M+m)<br>rarr x_1=M/mx<br>:.Thebagwillreachthe⊥→matadistance(M/m)x towards left of the line it falls.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
A ball is thrown from a point in level with velocity u and at a horizontal distance r from the top os a tower of height h.
At what horizontal distance x from the foot of the tower does the ball hit the ground ?
View SolutionIf a small orifice is made at a height of 0.25 m from the ground, the horizontal range of water stream will be : -
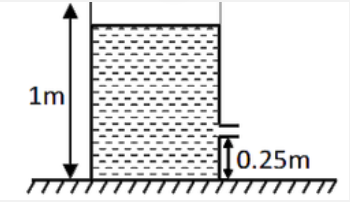
View SolutionDrops of water fall from the roof of a building 9m. High at regular intervals of time, the first drop reaching the ground at the same instant fourth drop starts to fall. What are the distance of the second and third drops from the roof?
View SolutionDrops of water fall at regular intervals from the roof of a building of height H = 5 m, the first drop strikes the ground at the same moment when the fifth drop detaches itself from the roof. Then ratio of distances as first drop reaches the ground are :
View Solution
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionA particle of mass 'm' is moving in horizontal circle inside a smooth inverted fixed vertical cone above height 'h' from apex. Angle of cone is θ, then
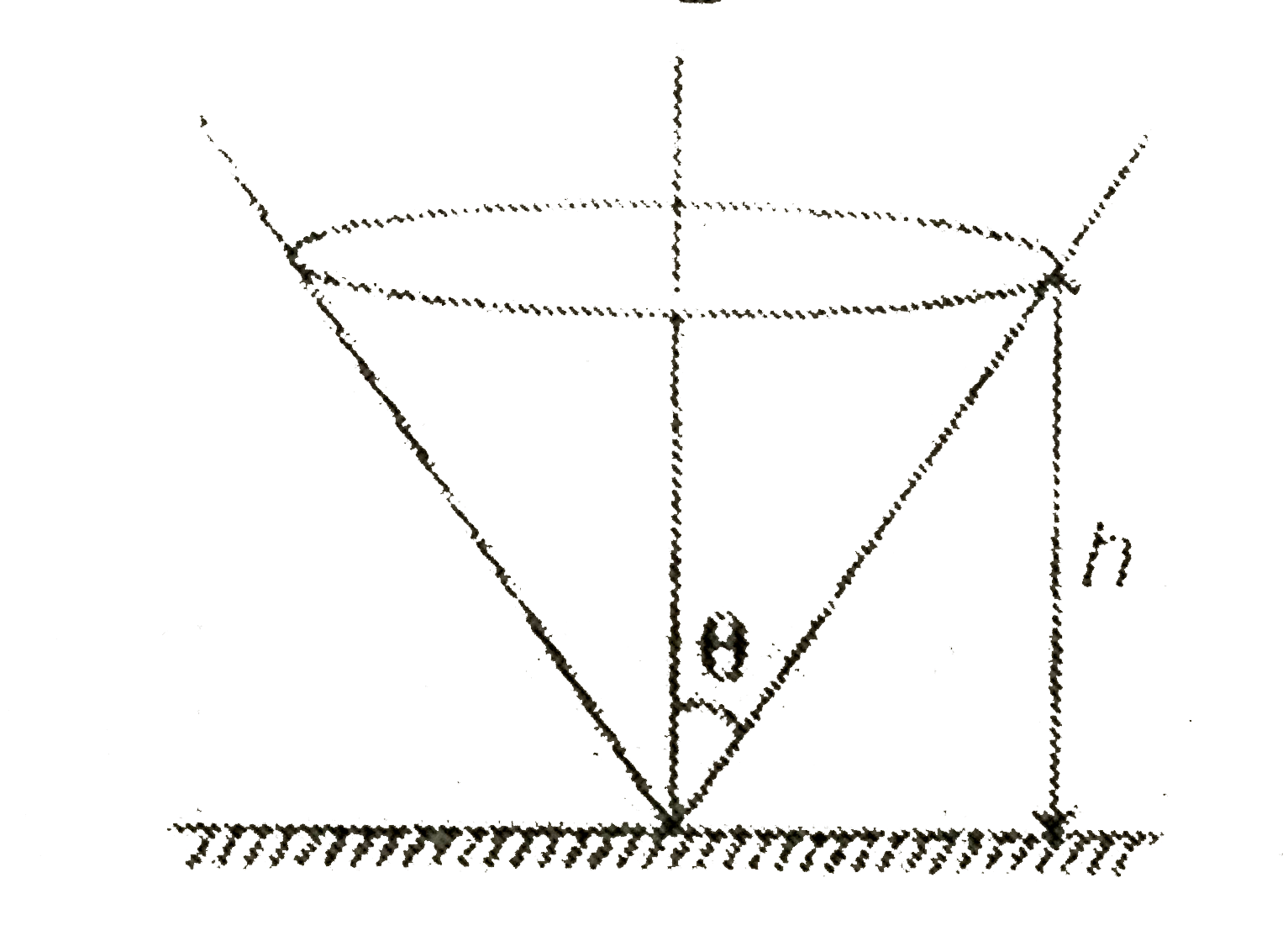
View SolutionA body is thrown horizontally with a velocity of v m/s from the top of a tower of height 2h reaches the ground in 't' seconds. If another body double the mass is thrown horizontally with a velocity 5v m/s from the top of another tower of height 8h it reaches the ground in a time of
View SolutionA body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If a second body of mass 2m is projected horizontally from the top of a tower of height 2h, it reaches the ground at a distance 2x from the foot of the tower. The horizontal veloctiy of the second body is.
View SolutionA particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionA body is falling from height 'h' it takes t1 time to reach the ground. The time taken to cover the first half of height is:-
View Solution
