Question

A standing wave exists in string of length 150 cm fixed at both ends. The displacement amplitude of a point at a distance of 10 cm from one of ends if $5\sqrt{3}mm$. The distance between two nearest points, within the same loop having the same displacement amplitude of $5\sqrt{3}$ is 10 nm.
The maximum displacement amplitude of the particle in the string is,:

Options

A. `10sqrt(3)` cm
B. 15 cm
C. 20 cm
D. 30 cm

Answer

B

Explanation

Given displacement amplitude of a point 10 cm from end is `5sqrt(3)mm`.
Also distance with same loop between two point with
displacement amplitude `5sqrt(3)` is also 10 cm. Then
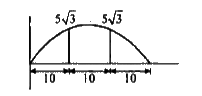By symmetry, `(lambda)/(2) = 30 cm`
`lambda = 60 cm`
Now `lambda rightarrow 2p rightarrow 60 cm`
`10 cm rightarrow (lambda)/(6) = (2pi)/(6) = (pi)/(3)`
`A sin "(pi)/(3) = 5sqrt(3)`
`A = (5sqrt(3))/(sqrt(3)//2) = 10 mm`
Since there will be 5 loops in string, string is in 4^(th) overtone. Potential energy of string will be zero at antinodes, which will be 15 cm from one end.