A standing wave is produced on a string on a string clamped at one end and free at the other. The length of the string
must be an integral multiple λ4
must be an integral multiple of λ2
must be an integral multiple of λ
may be an integral multiple of λ2
The correct Answer is:A
To solve the problem of determining the length of a string that produces a standing wave when one end is clamped and the other end is free, we can follow these steps:
1. Understanding the Setup:
- We have a string that is fixed at one end (clamped) and free at the other end. This setup allows for the formation of standing waves.
2. Identifying the Fundamental Frequency:
- For a string that is fixed at one end and free at the other, the fundamental frequency (first harmonic) can be described by the equation:
L=(2n+1)λ4
- Here, L is the length of the string, n is the harmonic number (0, 1, 2,...), and λ is the wavelength.
3. Understanding the Harmonics:
- The harmonic number n can take values starting from 0. Therefore, the possible lengths of the string for different harmonics can be calculated:
- For n=0: L=1λ4
- For n=1: L=3λ4
- For n=2: L=5λ4
- This shows that the lengths of the string correspond to odd multiples of λ4.
4. Conclusion:
- The length of the string must be an odd integral multiple of λ4. Therefore, we can conclude that the length of the string can be expressed as:
L=(2n+1)λ4
- This means that the string can have lengths such as λ4, 3λ4, 5λ4, etc.
Final Answer:
The length of the string must be an odd integral multiple of λ4.
---
- We have a string that is fixed at one end (clamped) and free at the other end. This setup allows for the formation of standing waves.
- For a string that is fixed at one end and free at the other, the fundamental frequency (first harmonic) can be described by the equation:
L=(2n+1)λ4
- Here, L is the length of the string, n is the harmonic number (0, 1, 2,...), and λ is the wavelength.
- The harmonic number n can take values starting from 0. Therefore, the possible lengths of the string for different harmonics can be calculated:
- For n=0: L=1λ4
- For n=1: L=3λ4
- For n=2: L=5λ4
- This shows that the lengths of the string correspond to odd multiples of λ4.
- The length of the string must be an odd integral multiple of λ4. Therefore, we can conclude that the length of the string can be expressed as:
L=(2n+1)λ4
- This means that the string can have lengths such as λ4, 3λ4, 5λ4, etc.
The length of the string must be an odd integral multiple of λ4.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises57videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -120videos
WAVE MOTION AND WAVES ON A STRING
- BOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer9videos
THE FORCES
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer16videos
WORK AND ENERGY
Similar Questions
A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1.0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ?
View SolutionA string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160Nm−1 and is stretched by 1.0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring ?
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View SolutionIn a standing transerse wave on a string :
View SolutionA 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 220ms−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0.5 cm, write a suitable equation describing the motion.
View SolutionThe vibrations from an 800 Hz tuning fork set up standing waves in a string clamped at both ends. The wave speed in the string is known to be 400m/s for the tension used. The standing wave is observed to have four antinodes. How long is the string?
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
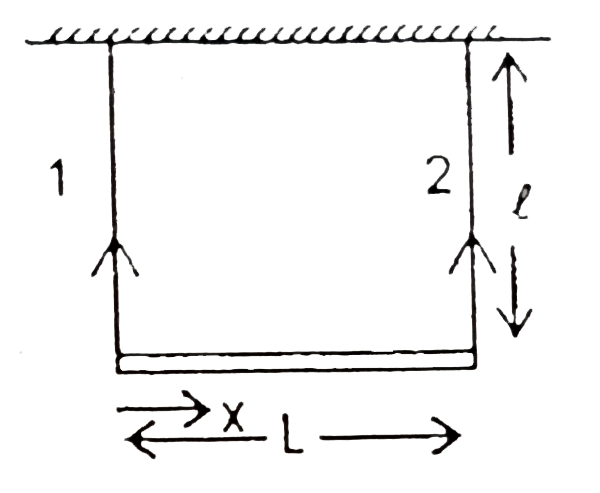 View Solution
View SolutionA standing wave of time period T is set up in a string clamped between two rigid supports, At t=0 antinode is at its maximum displacement 2A.
View SolutionAssertion:- Transvers waves are produced in a very long string fixed at one end. Near the free end only progressive wave is observed.
Reason:- Energy of reflected wave does does not reach the free end.View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View Solution

