A steady current goes through a wire loop having shape of a right angle triangle with . If the magnitude of the magnetic field at due to this loop is , find the value of .
1
5
10
7
The correct Answer is:D
To find the value of K in the equation for the magnetic field at point P due to the wire loop PQR, we will follow these steps:
Step 1: Understand the Geometry of the Triangle
The triangle PQR is a right triangle with:
- PQ=3x
- PR=4x
- QR=5x
Step 2: Calculate the Area of Triangle PQR
The area A of triangle PQR can be calculated using the formula:
A=12×base×height
Here, we can take PQ as the base and PR as the height:
A=12×3x×4x=6x2
Step 3: Find the Lengths PD and QD
To find the distances PD and QD, we will drop a perpendicular from point D on line QR to point P.
1. Using the area of triangle PDR:
APDR=12×PD×DR
Since DR is the height from D to R, we can express the area in terms of PD:
APDR=12×PD×5x
Equating the areas gives:
12×PD×5x=6x2
Solving for PD:
PD=12x5
2. Finding QD:
Using Pythagoras theorem in triangle PQD:
PQ2=PD2+QD2
Substituting the known values:
(3x)2=(12x5)2+QD2
Simplifying gives:
9x2=144x225+QD2
Rearranging and solving for QD:
QD2=9x2−144x225=225x2−144x225=81x225
Thus,
QD=9x5
Step 4: Calculate DR
Now, DR can be calculated as:
DR=QR−QD=5x−9x5=25x−9x5=16x5
Step 5: Calculate the Magnetic Field at Point P
The magnetic field B at point P due to the wire loop can be calculated using the Biot-Savart Law:
B=μ0I4π∫dLsin(θ)r2
Since B at point P is due to segment QR only:
B=μ0I2π(PD⋅sin(ϕ1)+PD⋅sin(ϕ2)r)
Step 6: Substitute Values and Simplify
Substituting the values of PD, sin(ϕ1), and sin(ϕ2):
sin(ϕ1)=QDPQ=9x53x=35
sin(ϕ2)=DRPR=16x54x=45
Thus,
B=μ0I2π(12x5(35+45))
=μ0I2π(12x5⋅75)=84μ0I50πx
Step 7: Compare with Given Expression
The expression given is:
B=kμ0I48πx
Setting the two expressions equal:
8450=k148
Thus,
k=84⋅4850=403250=80.64
Final Answer
The value of K is 7.
The triangle PQR is a right triangle with:
- PQ=3x
- PR=4x
- QR=5x
The area A of triangle PQR can be calculated using the formula:
A=12×base×height
Here, we can take PQ as the base and PR as the height:
A=12×3x×4x=6x2
To find the distances PD and QD, we will drop a perpendicular from point D on line QR to point P.
APDR=12×PD×DR
Since DR is the height from D to R, we can express the area in terms of PD:
APDR=12×PD×5x
Equating the areas gives:
12×PD×5x=6x2
Solving for PD:
PD=12x5
Using Pythagoras theorem in triangle PQD:
PQ2=PD2+QD2
Substituting the known values:
(3x)2=(12x5)2+QD2
Simplifying gives:
9x2=144x225+QD2
Rearranging and solving for QD:
QD2=9x2−144x225=225x2−144x225=81x225
Thus,
QD=9x5
Now, DR can be calculated as:
DR=QR−QD=5x−9x5=25x−9x5=16x5
The magnetic field B at point P due to the wire loop can be calculated using the Biot-Savart Law:
B=μ0I4π∫dLsin(θ)r2
Since B at point P is due to segment QR only:
B=μ0I2π(PD⋅sin(ϕ1)+PD⋅sin(ϕ2)r)
Substituting the values of PD, sin(ϕ1), and sin(ϕ2):
sin(ϕ1)=QDPQ=9x53x=35
sin(ϕ2)=DRPR=16x54x=45
Thus,
B=μ0I2π(12x5(35+45))
=μ0I2π(12x5⋅75)=84μ0I50πx
The expression given is:
B=kμ0I48πx
Setting the two expressions equal:
8450=k148
Thus,
k=84⋅4850=403250=80.64
The value of K is 7.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS
6 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - ASSERTION & REASON
15 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A current loop, carrying a current of 5.0 A, is in the shape of a right triangle with sides 30,40, and 50 cm. The loop is in a uniform magnetic field of magnitude 80 mT whose direction is parallel to the current in the 50 cm side of the loop. Find the magnitude of (a) the magnetic dipole moment of the loop and (b) the torque on the loop.
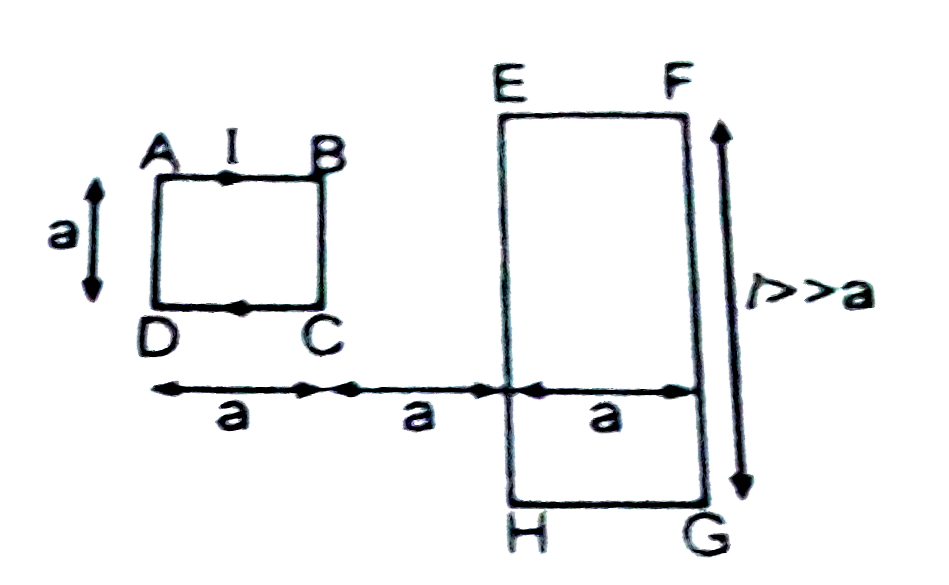
View SolutionIn the figure shown two loops ABCD &EFGH are in the same plane. The smaller loop carries time varying current I=bt, where b is a positive constant and t is time. The resistance of the smaller loop is r and that of the larger loop is R : (Neglect the self inductance of large loop ). The magnetic force on the loop EFGH due to loop ABCD is μ20Iabxπ2Rln43 . Find the value of x.
View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionCurrent I flows through a long conducting wire bent at right angle as shown in Fig. Find the magnetic field at point P on the right angle bisector of the angle XOY at distance r form O.

View SolutionIf one of the values of x of the equation 2x2−6x+k=0 be 12(a+5i), find the values of a and k.
View SolutionA straight section PQ of a circuit lise along the X-axis from x=−a2 to x=a2 and carriers a steady current i. The magnetic field due to the section PQ at a point X=+a will be
View SolutionA square metallic loop of side l is placed near a fixed long wire carrying a current i(figure).The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop.The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is μ0ivxπ.Find out value of x.

View SolutionA circular wire loop of radius R is placed in the X-Y plane with its centre at the origin. The loop carries a current I in the clockwise direction when viewed from a point on the positive Z-axis. A uniform magnetic field →B=B0(ˆi+√3ˆj2) exists in the region x>R√32. The magnitued of the magnetic force on the loop due to the magnetic field is B0IRn. The value of n is______________.
View SolutionA spiral loop has inner radius 10 cm and outer radius 20 cm and carries current 1A in each turn. The total no. of turn in loop is 100. A small rectangular loop of area 2cm2 carries current 0.05 A is placed at the centre of loop. If magnitude of potential energy of rectangular loop is xμ0Ln2400J. then find out the value of x

View SolutionA wire of length l carries a current I along the x-asis. A magnetic field exists which is given as →B=B0(→i+→j+→k) T. find the magnitude of the magnetic force acting on the wire.
View Solution
