A current I=10A flows in a ring of radius r0=15cm made of a very thin wire. The tensile strength of the wire is equal to T=1.5N. The ring is placed in a magnetic field, which is perpendicular to the plane of th ering so that the forces tend to break the ring. Find B ( in T) at which the ring is broken.
0.5 T
1 T
2 T
2.5 T
The correct Answer is:B
To solve the problem, we need to find the magnetic field B at which the ring breaks due to the tensile strength of the wire. Here’s a step-by-step solution:
Step 1: Understand the Forces Acting on the Ring
When a current I flows through the ring in a magnetic field B, a magnetic force acts on the wire. This force tends to stretch the wire, and we need to find the magnetic field strength at which this force equals the tensile strength T of the wire.
Step 2: Calculate the Magnetic Force on the Ring
The magnetic force F acting on a segment of the ring can be expressed as:
F=B⋅I⋅L
where:
- B is the magnetic field strength,
- I is the current flowing through the wire,
- L is the length of the wire segment in the magnetic field.
For a ring, the length L is the circumference of the ring:
L=2πr0
where r0 is the radius of the ring.
Step 3: Substitute the Length of the Ring
Substituting the expression for L into the force equation, we have:
F=B⋅I⋅(2πr0)
Step 4: Set the Magnetic Force Equal to the Tensile Strength
The ring will break when the magnetic force equals the tensile strength T:
B⋅I⋅(2πr0)=T
Step 5: Solve for the Magnetic Field B
Rearranging the equation to solve for B:
B=TI⋅(2πr0)
Step 6: Substitute the Given Values
Now, we can substitute the known values:
- T=1.5N
- I=10A
- r0=15cm=0.15m
Substituting these values into the equation:
B=1.510⋅(2π⋅0.15)
Step 7: Calculate the Value
Calculating the denominator:
2π⋅0.15≈0.942m
Now substituting this back into the equation for B:
B=1.510⋅0.942≈1.59.42≈0.159T
Step 8: Final Calculation
Calculating the final value gives:
B≈0.159T
Conclusion
The magnetic field strength at which the ring will break is approximately 0.159T.
---
When a current I flows through the ring in a magnetic field B, a magnetic force acts on the wire. This force tends to stretch the wire, and we need to find the magnetic field strength at which this force equals the tensile strength T of the wire.
The magnetic force F acting on a segment of the ring can be expressed as:
F=B⋅I⋅L
where:
- B is the magnetic field strength,
- I is the current flowing through the wire,
- L is the length of the wire segment in the magnetic field.
L=2πr0
where r0 is the radius of the ring.
Substituting the expression for L into the force equation, we have:
F=B⋅I⋅(2πr0)
The ring will break when the magnetic force equals the tensile strength T:
B⋅I⋅(2πr0)=T
Rearranging the equation to solve for B:
B=TI⋅(2πr0)
Now, we can substitute the known values:
- T=1.5N
- I=10A
- r0=15cm=0.15m
B=1.510⋅(2π⋅0.15)
Calculating the denominator:
2π⋅0.15≈0.942m
Now substituting this back into the equation for B:
B=1.510⋅0.942≈1.59.42≈0.159T
Calculating the final value gives:
B≈0.159T
The magnetic field strength at which the ring will break is approximately 0.159T.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXEMPLAR PROBLEMS6videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - ASSERTION & REASON15videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason15videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
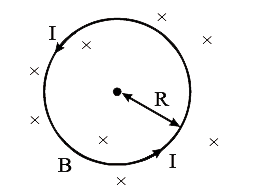
A current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
 View Solution
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA ring of radius R is rolling on a horizontal plane with constant velocity v. There is a constant and uniform magnetic field B which is perpendicular to the plane of the ring. Emf across the lowest point A and right-most point C as shown in the figure will
 View Solution
View SolutionA vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
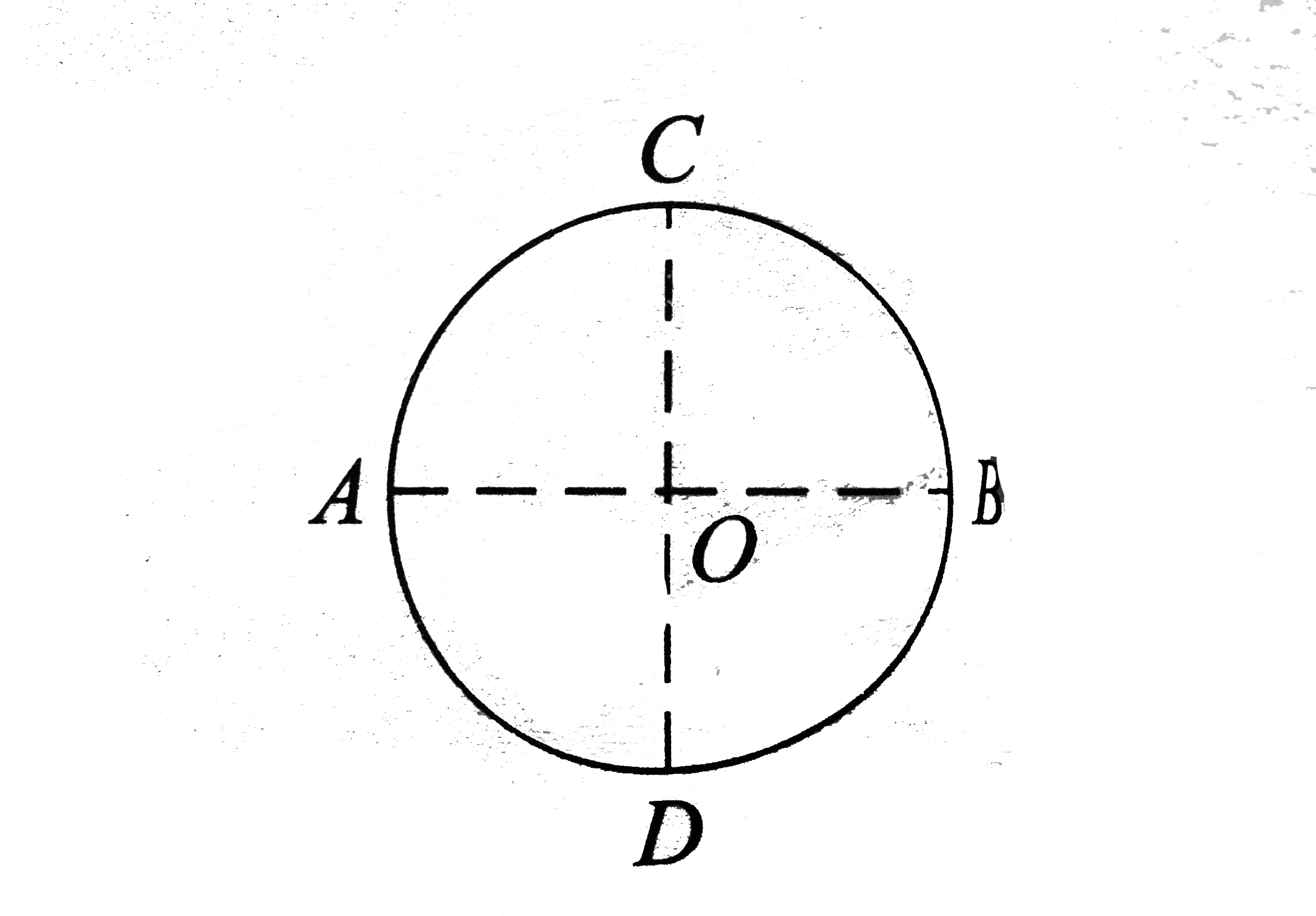 View Solution
View SolutionCharge Q is uniformly distributed on a thin insulating ring of mass m which is initially at rest. To what angular velocity will the ring be accelerated when a magnetic field B, perpendicular to the plane of the ring, is switched on ?
View SolutionA ring of radius R is made of a thin wire of material of density ρ, having cross-section area a and Young's modulus y. The ring rotates about an axis perpendicular to its plane and through its centre. Angular frequency of rotation is ω.
The tension in the ring will beView SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
 View Solution
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is
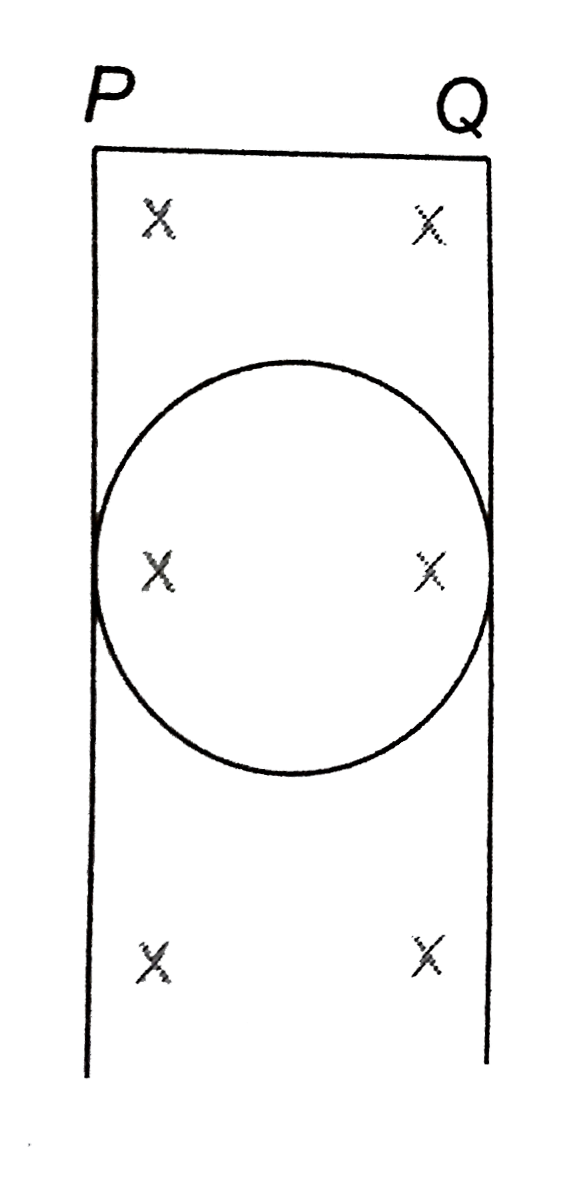 View Solution
View SolutionA vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is
 View Solution
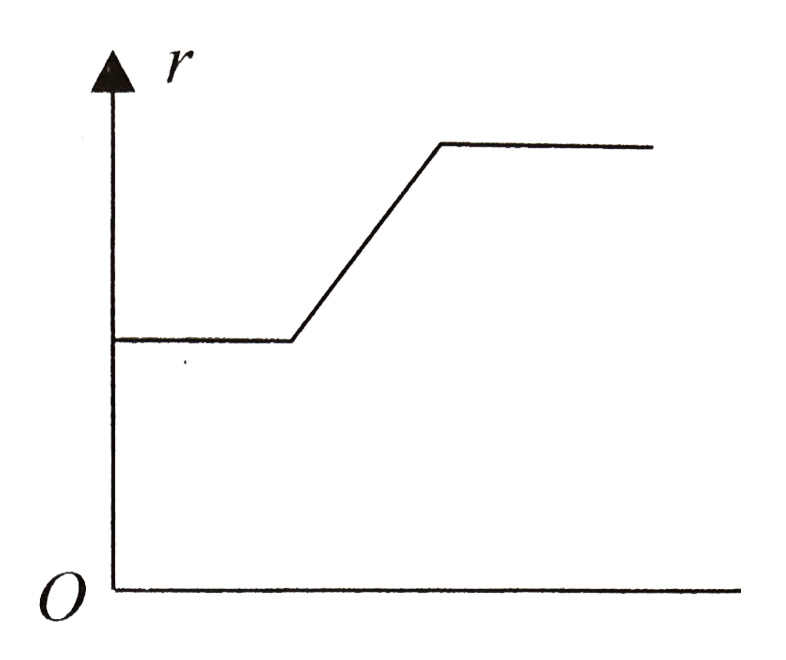
View SolutionRadius of a circular ring is changing with time and the coil is placed in uniform magnetic field perpendicular to its plane. The variation of 'r' with time 't' is shown in Fig. Then induced emf e with time t will be best represented by
 View Solution
View Solution

