A stone of mass m tied to one end of a string is revolved in a vertical circle of radius R the net forces at the lowest (FL and highest (FH) points of the circle directed vertically downwards are :
(a) FL=mg−T1FH=mg+T2
(b) FL=mg+T1,FH=mg−T2
(c) FL=mg+T1−mυ21R,FH=mg−T2+mυ21R
(d) FL=mg−T1−mυ21R,FH=mg+T2+mυ12R
Choose corret alternative T1,υ1 denote the tension and speed at the lowest point T2,υ2 denote corresponding valuse at the highest point .
The net force at the lowest point L is FL=(mg−T1 and the net force at the highest point H is FH=mg+T2 Thereforce alternative (a) is correct For details.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Additional Examples / Exercises
6 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Short Answer Questions
35 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Advanced problems for competitions
20 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
Knowledge Check
A main revolves a stone of mass m tied to the end of a string in a circle of radius R The net force at the lowest and height point of the circle directed vertical downward are
Here T1,T2 and (v1,v2) denote the tension in the string (and the speed of the stone) at the lowest and highest points, respectively.ALowest pointhighest pointmg−T1mg+T2BLowest pointhighest pointmg+T1mg−T2CLowest pointhighest pointmg+T1−mv2rmg−T2+mv2rDLowest pointhighest pointmg−T1−m1v21Rmg+T+m1v21RA stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative] Lowest point Highest point
T1 and V1 denote the tension and speed at the lowest point T2 and V2 denote the corresponding values at the highest points.Amg−T1mg+T2Bmg+T1mg−T2Cmg+T1−(mv21)/Rmg−T+(mv21)/RDmg−T1−(mv21)/Rmg+t2+(mv21)/RAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F.
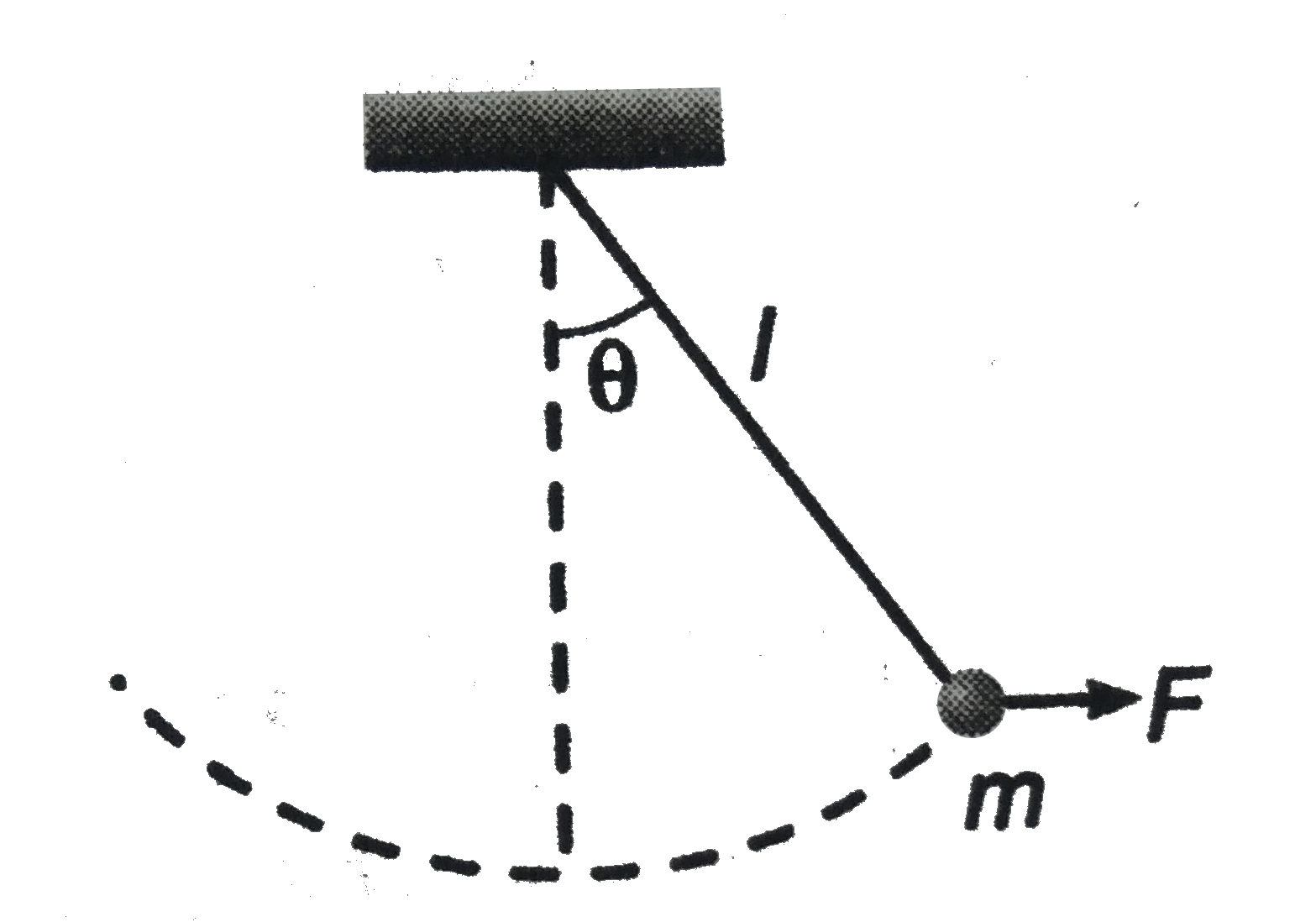 . Amgl(1+cosθ)Bmgl(1−cosθ)Cmgl(1−cosθ)Dmgl(1+cosθ)
. Amgl(1+cosθ)Bmgl(1−cosθ)Cmgl(1−cosθ)Dmgl(1+cosθ)
The length of a metal wire is l1 when the tension in it is F1 and l2 when the tension becomes F2. Find the natural length of wire.
View SolutionA particle of mass m is suspended from a string so that it can move in a circular path in vertical plane. It is given v=3√glat the bottom most point. Match the values of tension in string at A,B,C,D

Column IColumn II(A) TA(P) 10 mg ),((B) T_(B),,(Q)7mg),((C) T_(C),,(R)4mg),((D) T_(D),,(S)5mg),(,,(T)5.5mg
View SolutionUnder the action of load F1, the length of a string is L1 and that under F2, is L2. The original length of the wire is
View SolutionTwo forces of mangitude F1 and F2 are acting on an object.The magnitude of the net force Fnet on the object will be in the range.
View SolutionConsider three blocks of masses m1,m2,m3 interconnected by strings which are pulled by a common force F on a frictionless horizontal table as in the figure. The tension T1andT2 are also indicated

a) T2>T1 if m2>m1
b) T2=T1 if m2=m1
c) T2>T1 always
d) acceleration of the system=Fm1+m2+m3
View Solution
