A string with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of 2m from the wall, has a point mass M of 2kg attached to it at a distance of 1m from the wall. A mass m of 0.5kg is attached to the free end. The system is initially held at rest so that the stirng is horizontal between wall and pulley and vertical beyond the pulley as shown in figure.

What will be the speed with which point mass M will hit the wall when the system is released? (g=10ms−2)
When M strikes the wall, the vertically downward component of its displacement from initial position is 1m and its distance from pulley B is, C′B=√12+22=√5m.
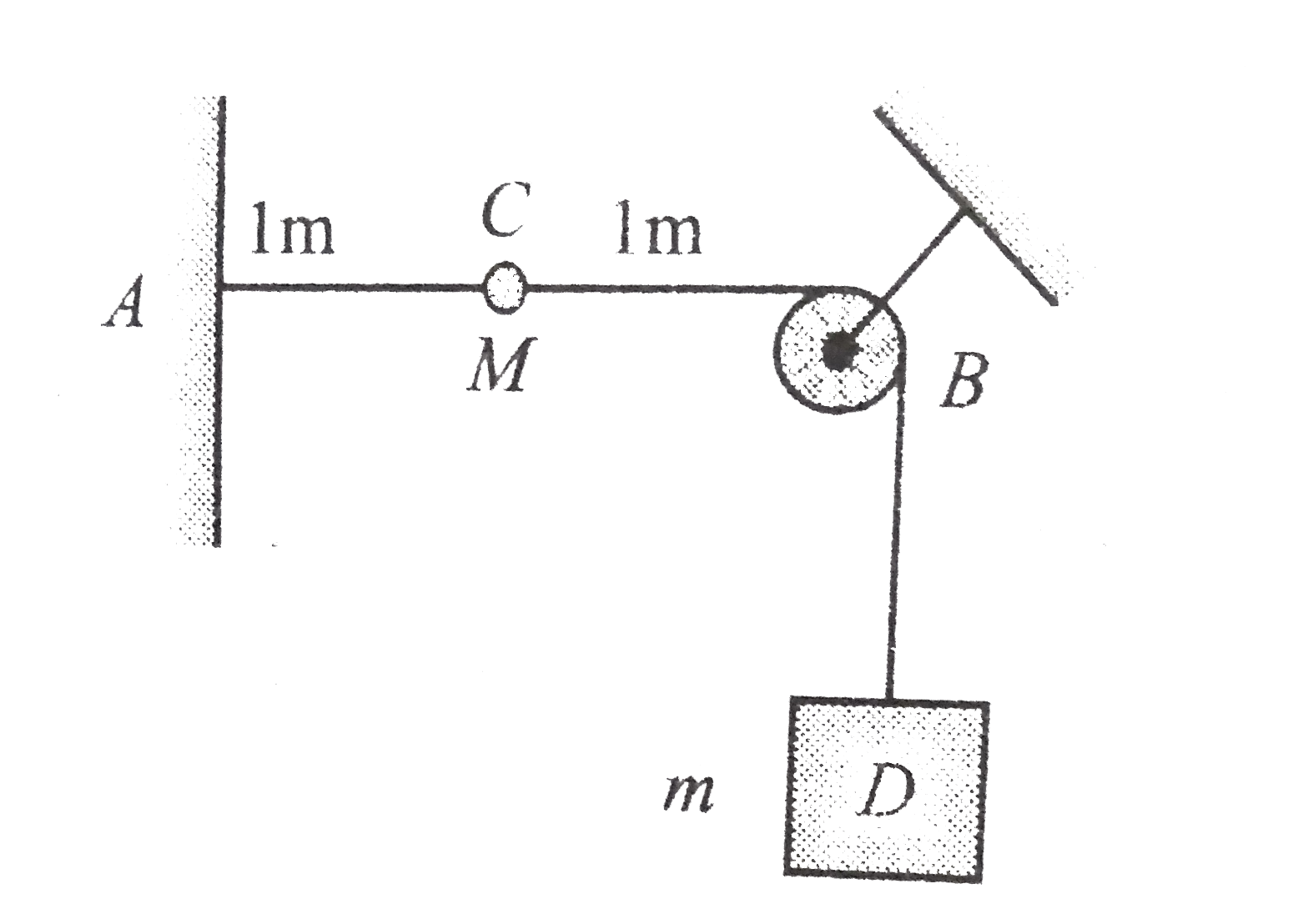
while its initial distance from the pulley was CB=1m. It means vertically upward displacement of mass m is (√5−1)m,
Let M strike the wall with velocity v, Since, string between two blocks always remains taut, therefore at any instant speed of m is equal to that component of velocity of M which is along the string C′B. Hence, the velocity of m when M strikes the wall is v=cosθ, where
cosθ=2√5
According to the law of conservation of energy the loss of potential energy of M
=Increase in PE of m+KE of M=KE of m
Mg×1=mg(√5−1)+12m(vcosθ)2
v=5√5−√56ms−1=3.39ms−1
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Discuss whether any work is being done by each of the following agents and, if so, whether the work is positive or negative: (a) a chicken scratching the ground, (b) a person studying, (c) a crane lifting a bucket of concrete, (d) the gravitational force on the bucket in part (c), and (e) the leg muscles of a person in the act of sitting down.
View SolutionThe kinetic energy of a body is increased by 21%. What is the percentage increase in the magnitude of linear momentum of the body?
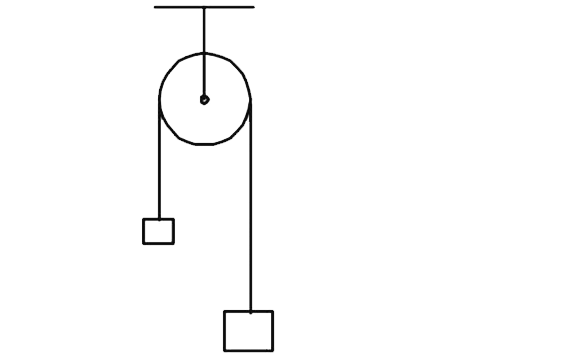
View SolutionA light inextensible string that gas over a smoth fixed polley as shown in the figure connect two blocks of mases it 0.36 kg and 0.72 kg Taking g=10ms−2 , find the work done by the string on the block of mass 0.36 kg doring the first second after the system is released from rest ,
View SolutionWhich of the following statements is/ are correct(Figure)
View SolutionA string with one end fixed on a right well , passing over a fixed frictionless pulley at a distance of 2 m from the well , has a point mass M = 2kg attached to the it at a distance of I m from the well . A mass m= 0.5 kg attached at the free end is field at rest as this the string is horizontal between the wall and the pulley when will be the speed with which the mass M with hit the well when the mass m is released ?
View SolutionIn the figure shown, a spring mass system is placed on a horizontal smooth surface in between two vertical rigid walls W_(1) and W_(2) . One end of spring is fixed with wall W_(1) and other end is attached with mass m which is free to move. Initially, spring is tension free and having natural length l_(0) . Mass m is compressed through a distance a and released. Taking the collision between wall W_(2) and mass m as elastic and K as spring constant, the average force exerted by mass m on wall W_(2) in one oscillation of block is
View SolutionA string with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of 2m from the wall, has a point mass M of 2kg attached to it at a distance of 1m from the wall. A mass m of 0.5kg is attached to the free end. The system is initially held at rest so that the stirng is horizontal between wall and pulley and vertical beyond the pulley as shown in figure.

What will be the speed with which point mass M will hit the wall when the system is released? (g=10ms−2)
View SolutionA string with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of 2 m from the wall, has a point mass M of 2 kg attached to it at a distance of 1 m from the wall. A mass in of 0.5 kg is attached to the free end. The system is initially held at rest so that the string is horizontal between wall and pulley and vertical beyond the pulley as shown in Fig. The system is released from the rest from the position as shown. The ratio of velocity of M and m when M strikes the wall is
View SolutionA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R figure a. Assume the stirng does not slide over the pulley. Find the acceleration of the block when released.
View SolutionThe masses (M+m) and (M-m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are relased from rest the acceleraion of the system is .
View SolutionA uniform cubical block of mass M is attached to a pulley. One end of a string, passing over the pulley is fixed to a light pole while is fixed on the bigger block and its another end is attached to a block of mass m as shown in figure. The maximum value of the mass m so that the block does not topple is : (string and pulley are ideal)

View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View Solution20 किग्रा द्रव्यमान की एक 3 मी. लंबी सीढ़ी एक घर्षण विहीन दीवार के साथ झुकाकर टिकाई गई है जैसा कि चित्र में दर्शाया गया है । इसका निचला सिरा फर्श पर दीवार से 1 मी. की दूरी पर है । दीवार और फर्श के प्रतिक्रिया बल ज्ञात कीजिए ।
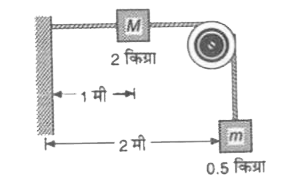
View Solutionएक डोरी, जिसका एक सिरा दृढ दीवार से बंधा है, दीवार से 2 मी दूर घर्षणहीन स्थिर घिरनी के ऊपर से गुजरती है। दीवार से 1 मी दुरी डोरी से एक बिंदु द्रव्यमान M=2 किग्रा बंधा ह। डोरी के मिक्त सिरे से बंधा एक द्रव्यमान m=0.5 किग्रा विरामावस्था में रखा गया है जिससे की दीवार तथा घिरनी के बिच डोरी क्षैतिज है तथा घिरनी के दूसरी और उर्ध्वार्धर है। जब द्रव्यमान m छोड़ते है, तब द्रव्यमान M के दीवार से टकराने की चाल क्या होगी ?
View SolutionA pulley fixed to the ceiling carries a string with blocks of masses m and 3 m attached to its ends. The masses of string and pulley are negligible. When the system is released the acceleration of centre of mass will be
View SolutionTwo masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
View Solution
