A super-ball of mass m is to bounce elastically back and forth between two rigid walls at a distance d from each other. Neglecting gravity and assuming the velocity of super-ball to be v0 horizontally, the average force being exerted by the super-ball on each wall is
12mv20d
mv20d
2mv20d
4mv20d
To solve the problem, we need to find the average force exerted by the super-ball on each wall as it bounces back and forth between two rigid walls. Here's a step-by-step solution:
Step 1: Understand the motion of the super-ball
The super-ball is moving horizontally between two walls that are a distance d apart. It travels back and forth with an initial velocity v0.
Hint: Visualize the motion of the ball between the two walls to understand the direction changes upon collision.
Step 2: Calculate the time taken for one complete round trip
The ball travels a distance of d to one wall and then d back to the original position, making a total distance of 2d. The time taken for this round trip can be calculated using the formula:
Time for one round trip=Total distanceVelocity=2dv0
Hint: Remember that the time taken is the total distance divided by the speed.
Step 3: Determine the number of collisions with each wall per second
The number of round trips (or collisions with each wall) per second can be calculated as:
Number of collisions per second=1Time for one round trip=v02d
Hint: Think about how many times the ball hits a wall in one second based on its speed and the distance between the walls.
Step 4: Calculate the change in momentum during a collision
When the ball collides with a wall, it reverses its velocity. The change in momentum (ΔP) for one collision can be calculated as:
ΔP=m(v0−(−v0))=m(v0+v0)=2mv0
Hint: Consider the direction of the velocity before and after the collision to find the change in momentum.
Step 5: Calculate the average force exerted on the wall
The average force (F) exerted by the super-ball on each wall can be calculated using the formula:
F=Rate of change of momentum=Number of collisions per second×ΔP
Substituting the values we found:
F=(v02d)×(2mv0)=mv20d
Hint: Use the relationship between force, momentum, and time to derive the average force.
Final Answer
The average force exerted by the super-ball on each wall is:
F=mv20d
The super-ball is moving horizontally between two walls that are a distance d apart. It travels back and forth with an initial velocity v0.
The ball travels a distance of d to one wall and then d back to the original position, making a total distance of 2d. The time taken for this round trip can be calculated using the formula:
Time for one round trip=Total distanceVelocity=2dv0
The number of round trips (or collisions with each wall) per second can be calculated as:
Number of collisions per second=1Time for one round trip=v02d
When the ball collides with a wall, it reverses its velocity. The change in momentum (ΔP) for one collision can be calculated as:
ΔP=m(v0−(−v0))=m(v0+v0)=2mv0
The average force (F) exerted by the super-ball on each wall can be calculated using the formula:
F=Rate of change of momentum=Number of collisions per second×ΔP
Substituting the values we found:
F=(v02d)×(2mv0)=mv20d
The average force exerted by the super-ball on each wall is:
F=mv20d
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
n balls each of mass m impinge elastically each second on a surface with velocity u. The average force experienced by the surface will be
View SolutionA particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
View SolutionA cricket ball of mass 150 kg is moving with a velocity of 12m/s and is hit by a bat so that ball is turned back with a velocity of 20m/s . The force of the blow acts for 0.01 s on the ball . Find the average force exerted by the bat on the ball.
View SolutionA bead of mass m and diameter d is sliding back and forth with velocity v on a wire held between two right walls of length L. Assume that th ecollisions with the wall are perfectly elastic and ther is no friction. The average force that the bouncing bead exerts on the one of the walls is :_
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionA particle of mass m is moving horizontally with a constant velocity v towards a rigid wall that is moving in opposite direction with a constant speed u. Assuming elastic impact between the particle and wall, the work done by the wall in reflecting the particle is equal to
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
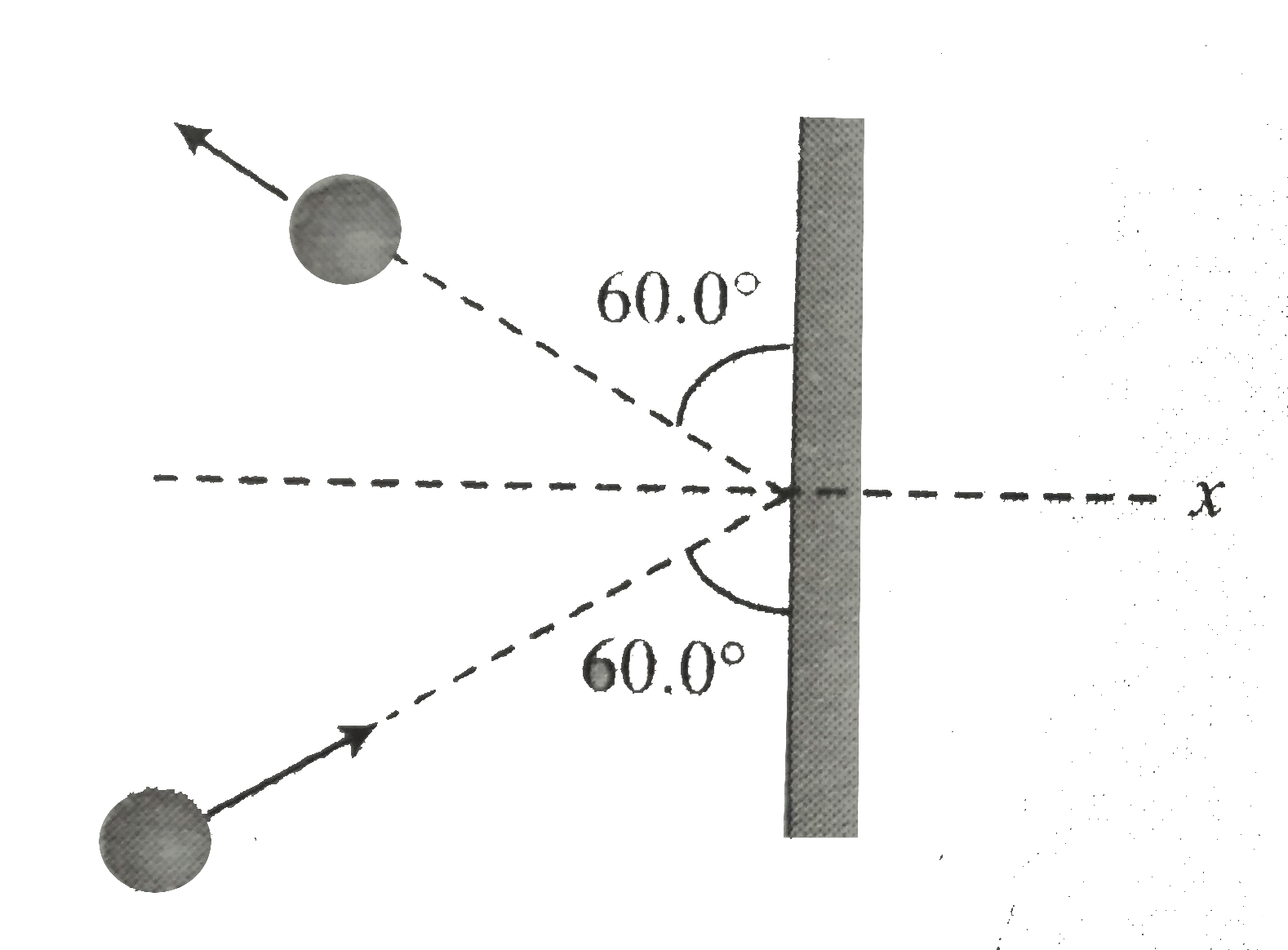
View SolutionA 150 g ball, moving horizontally at 20m/s was hit straight back to bowler at 12m/s. If contact with bat lasted for 0.04 sec, then average force exerted by the bat on the ball is:-
View Solution
