A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. The man has to reach the other shore at the point directly opposite to his starting point. If the reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
The correct Answer is:B, C
Velocity of man, Vm=3kmhr
BD= horizontal distance for resultant velocity R
X- component of resultant
R=5+3cosθ
t=0.53sinθ
Which is same of horizontal component of velocity.
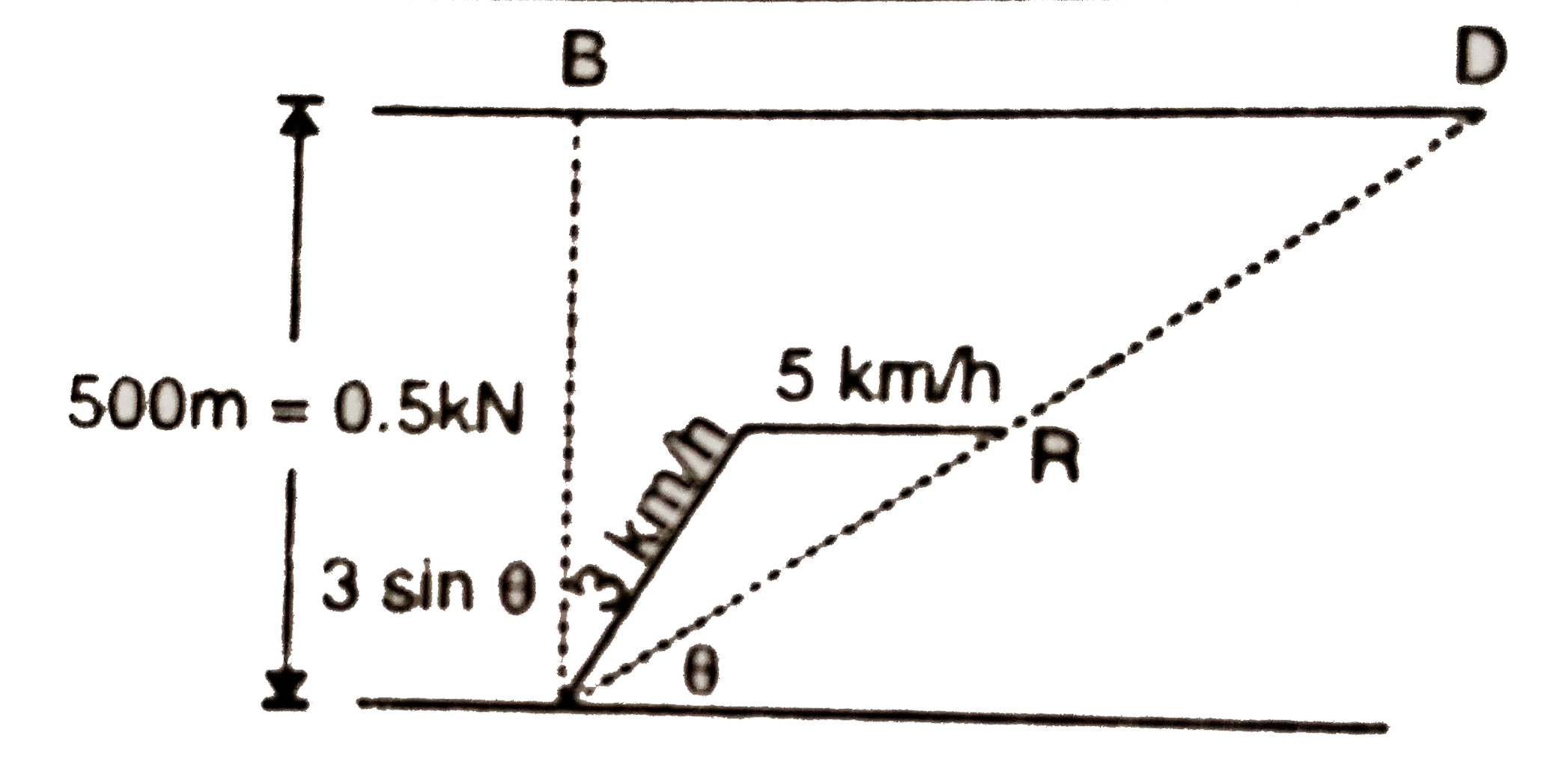
H=BD
=(5−3cosθ)(0.53sinθ)
=5+3cosθ6sinθ
For H to be minimum (dHdθ)=0
>ddθ(5+3cosθ6sinθ)=0
→18(sin2θ+cos2θ)−30cosθ=0
→30cosθ=18
→cosθ=−1830=−35
sinθ=√1−cos2θ0=45
∴H=5+3cosθ6sinθ
=5+3(35))6×45=25−924
=1624=23km.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective 2
10 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
Similar Questions
A swimmer wishes to cross a 500m wide river flowing at a rate 5km/hr. His speed with respect to water is 3km/hr. (a) If the heads in a direction making an angle θ with the flow, he takes to cross the river. (b) Find the shortest possible time to cross the river.
View SolutionA man wants to cross a river 500 m wide. His rowing speed in still water is 3 kmph. The river flows at a speed of 2 kmph. If the man's walking speed on the shore is 5kmph, (a) find the path he should take to get to the point directly opposite to his starting point in the shortest time. (b) How long does it take to get there?
View Solution
Knowledge Check
A swimmer wishes to cross a 500−m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
A10minB20minC6minD7.5minA man who swims at a speed of 5km/h wants to cross a 500m wide stream flowing at 4km/h and reach the point which is directly opposite to his starting point. If he reaches a point somewhere else he has to walk back to desitination, his walking speed being 2km/h. Find the minimum time in which he can reah his destination.
 A5 minB10 minC15 minD20 min
A5 minB10 minC15 minD20 minA swimmer whishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle θ with the perpendicular as shown in the figure.
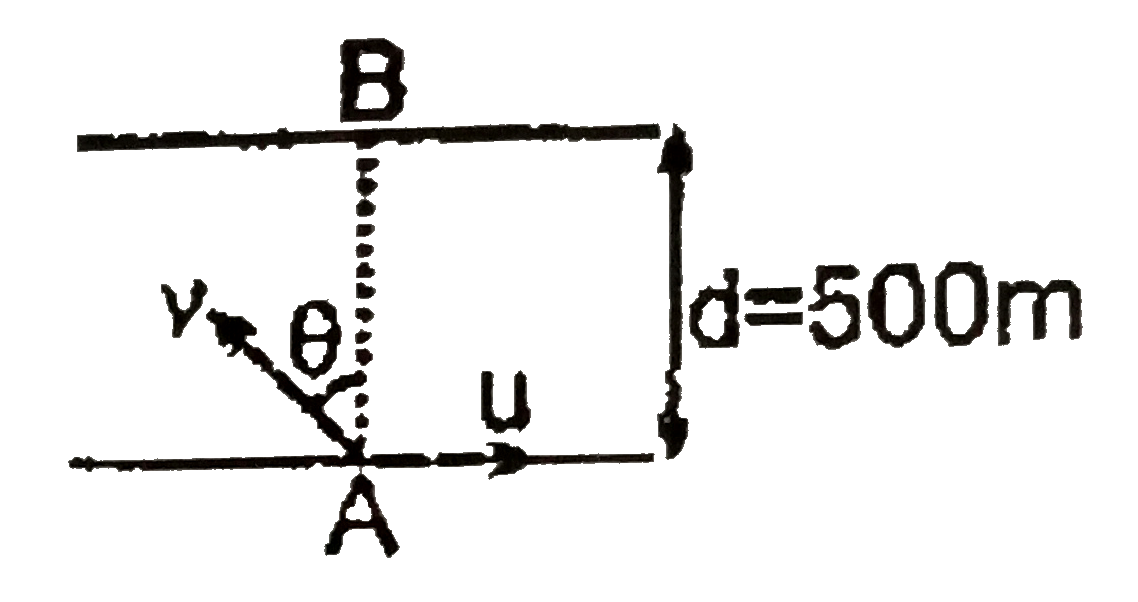
For u = 5 km/hrand v=3km//hr, the swimmer :ACan reach B in 7.5 min.BCan reach B in 6 min.CCan reach B in less than 6 minDCan never reach B
A man can row a boat with 4km/h in still water, if he is crossing a river where the current is 2 km/h.
(a) In what direction will his boat be holded, if he wants to reach a point on the other bank, directly opposite to starting point?
(b) If width of the river 4km, how long will the man take to cross the river, with the condition in part (a)?
(c) In what direction shou ld he heat the boat if he wants to cross the river in shorest time and what is this minimum time?
(d) How long will it take him to row 2 km up the stream and then back to his starting point?
View SolutionA man wishes to cross a river of width 120 m by a motorboat. His rowing speed in still water is 3m/s and his maximum walking speed is 1m/s. The river flows with velocity of 4m/s.
(a) Find the path which he should take to get to the point directly opposite to his starting point in the shortest time.
(b) Also, find the time which he takes to reach his destination.
View SolutionA boat can swim in still water with speed of 20 km/h . a river of width 500 meters flows with speed of 6 km./h. In what direction . . . . should the boat be pointed , so that it reaches the opposite bank at the point directly opposite the starting point ? Also find the time . . . . . taken. Is this the least time of crossing ?
View SolutionThe rowing speed of a man relative to water is 5kmh−1 and the speed of water flow is 3kmh−1. At angle to the river flow should he head if he wants to reach a point on the other bank, directly opposite to starting point ?
View SolutionA man can swim with a speed v relative to water . There is a river of width d which is flowing at a speed u . A is the point on river bank from where he starts and B is point directly opposite to A on the other side of the river .
View Solution
