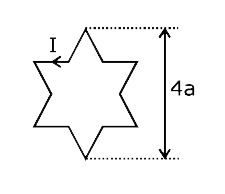
A symmetric star shaped conducting wire loop is carrying a steady state current I as shown in the figure. The distance between the diametrically opposite vertices of the star is 4a. The magnitude of the magnetic field at the center of the loop is

$\frac{μ_{0} I}{4 π a} 6 [\sqrt{3} - 1]$

$\frac{μ_{0} I}{4 π a} 6 [\sqrt{3} + 1]$

$\frac{μ_{0} I}{4 π a} 3 [2 - \sqrt{3}]$

$\frac{μ_{0} I}{4 π a} 3 [\sqrt{3} - 1]$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a

Updated on:21/07/2023

A square loop of side a carries a current $I$ . The magnetic field at the center of the loop is
A $\frac{2 μ_{0} I \sqrt{2}}{π a}$
B $\frac{μ_{0} I \sqrt{2}}{π a}$
C $\frac{4 μ_{0} I \sqrt{2}}{π a}$
D $\frac{μ_{0} I}{π a}$
A wire bent in the shape of a regular n-polygonal loop carries a steady current I. Let $l$ be the perpendicular distance of a given segment and R be the distance of vertex both from the centre of the loop. The magnitude of the magnetic field at the centre of the loop is given by -
A $\frac{n μ_{0} I}{2 π l} sin (π / n)$
B $\frac{n μ_{0} I}{2 π R} sin (π / n)$
C $\frac{n μ_{0} I}{2 π l} cos (π / n)$
D $\frac{n μ_{0} I}{2 π R} cos (π / n)$
A square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
Aindependent of L
Bproportional L
Cinversely proportional to L
Dlinearly proportional to L