A uniform magnetic field B exists in the region between x = 0 and x=3R2 (region 2 in the figure) pointing normally into the plane of the paper. A particle with charge +Qand momentum p directed along X-axis enters region 2 from region 1 at point P1(y=−R) . Which of the following option(s) is/are correct?

When the particle re-enters region 1 through the longest possible path in region 2, the magnitude of the change in its linear momenturn between P1 and the farthest point from Y- axis is p/√2.
For B=813pQR, the particle will enter region 3 through the point P2 on X - axis.
For a fixed B, particles of same charge Q and same velocity v, the distance between the point P1 and the point of re-entry into region 1 is inversely proportional to the mass of the particle.
For B>23pQR, the particle will re- enter region 1.
The correct Answer is:d
(a) In this case particle completes semicircular path and for the given time interval linear momentum changes its direction by 90∘.

Change in linear momentum can be written as
|Δ→p|=√2p
Hence option (a) is wrong .
(b) For given magnetic field (B=813pQR), radius of the circle described by the particle cna be written as follows :
R.=mvQB=pQ813pQR=13R8

y=R.−x=R.−√R.2−(3R/2)2
⇒y=13R8−√(13R8)2−(3R2)2
⇒y=13R8−√169R264−9R24
⇒y=13R8−√169R2−144R264=13R8−5R8=R
We can see that deviation of particle along Y-axis while travelling through the field region is R, hence according to given position of P1.andP2 , particle will pass through the point P2 , to enter the region 3. Hence option (b) is correct.
(c) If particle reenters region 1 then it describes semicircle inside region 2. Distance between P1 , and the point of reentry in region 1 is twice the radius of circle.
D=2r=2mvQB
We can see that required distance is directly proportional to mass, hence option (c) is wrong. (d) To reenter the region 1, radius of the circle must be less than the width of magnetic field region 2.
r<3R2⇒mvQB<3R2⇒pQB<3R2
⇒B>2p3RQ
Hence option (d) is correct.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
28 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (A. MULTIPLE CHOICE QUESTIONS)
38 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

View Solution
Knowledge Check
A uniform but time-varying magnetic field B (t) exists in a circular region of radius a and is directed into the plane of the paper as shown . The magnitude of the induced electric field at point P at a distance r from the centre of the circular region is
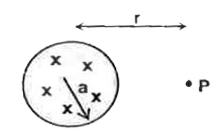 Ais zeroBproportional to rCproportional to 1/rDproportional 1/r2
Ais zeroBproportional to rCproportional to 1/rDproportional 1/r2A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
 Ais zeroBdecreases as 1rCIncreases as rDdecreases as 1r2
Ais zeroBdecreases as 1rCIncreases as rDdecreases as 1r2A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
 Ais zeroBDecreases as 1rCIncreases as rDDecreases as 1r2
Ais zeroBDecreases as 1rCIncreases as rDDecreases as 1r2
A positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionA uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown in the figure. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA uniform but time varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of paper as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region.

View Solution
