A system consists of three masses m1,m2 and my connected by a string passing over a pulley P. The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction = μ). The pulley is frictionless and of negligible mass. The downward acceleration of mass m, is mi (Assume m1=m2=m3=m)

g(1−gμ)9
2gμ3
g(1−2μ)3
g(1−2μ)2
The correct Answer is:C
Force of friction on mass
m2=μm2g
force of friction on mass
m3=μm3g
force of friction on mass
m3=μm3g
let a be common acceleration of the system
∴a=m1g−μm2g−μm3gm1+m2+m3
here m1=m2−m3−m
∴a=mg−μg−μgm+m+m=mg−2μmg3m=g(1−2μ)3
hence the downward acceleration of mass m1 is g(1−2μ)3

Topper's Solved these Questions
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - CHECK YOUR NEET VITALS
22 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
Similar Questions
A system consists of three masses m1 , m1 , m1 , m2 and m3 connected by a string passing over a pulley P . The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=mu) The pulley is frictionless and of negligible mass. The downward acceleration of m1 is (Assume m1=m2=m3=m).

View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
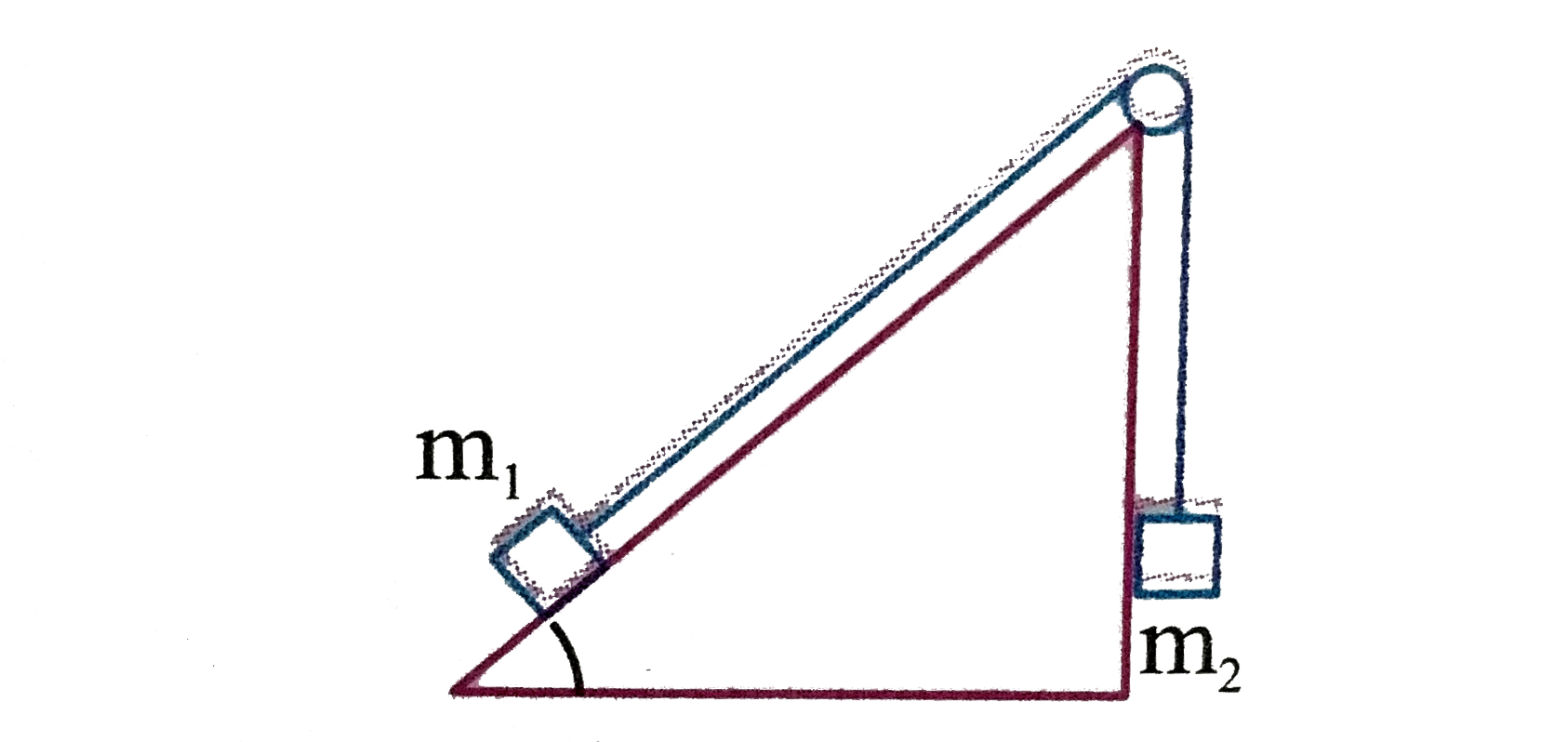
View Solution
Knowledge Check
A system consists of three masses m1,m2 and m3 connected by a string passing over a pulley P. The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=μ). The pulley is frictionless and of negligible mass. The downward acceleration of mass m1 is (assume, m1=m2=m3=m)
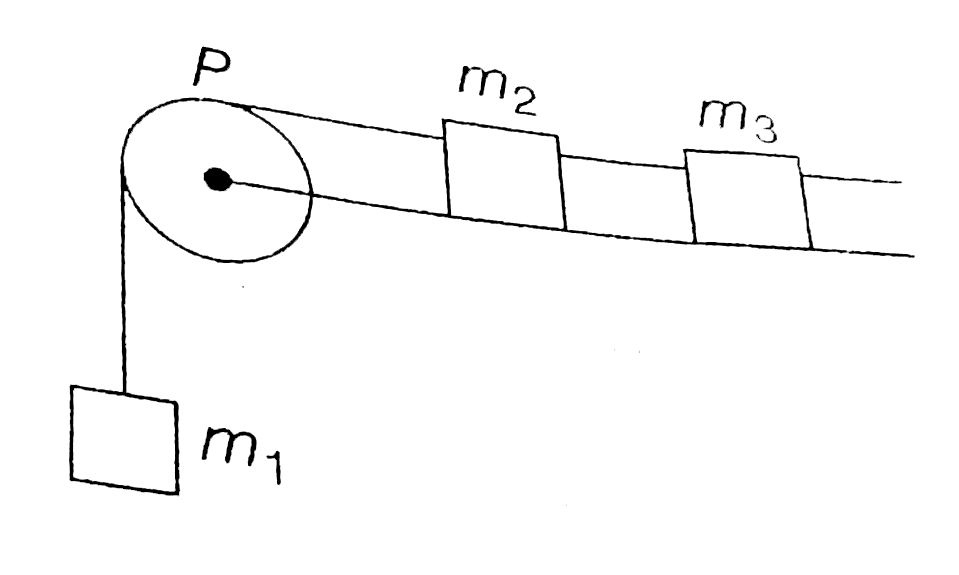 Ag(1−gμ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2
Ag(1−gμ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2A system consists of three masses m1 , m1 , m1 , m2 and m3 connected by a string passing over a pulley P . The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=μ) The pulley is frictionless and of negligible mass. The (Assume m1=m2=m3=m).
 Ag(1−2μ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2
Ag(1−2μ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2Two blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
 AIf m1=m2, the mass m1 first begin to move up inclined plane when the angle of inclination θ, then μ=secθ−tanθBIf m1=m2, then mass m1 first begin to side down the plane if μ=secθ−tanθ.CIf m1=2m2, then mass m1 first begins to slide down the plane if μ=2tanθ.DIf m1=2m2, then mass m1 first begins to slide down the plane if μ=tanθ−12secθ.
AIf m1=m2, the mass m1 first begin to move up inclined plane when the angle of inclination θ, then μ=secθ−tanθBIf m1=m2, then mass m1 first begin to side down the plane if μ=secθ−tanθ.CIf m1=2m2, then mass m1 first begins to slide down the plane if μ=2tanθ.DIf m1=2m2, then mass m1 first begins to slide down the plane if μ=tanθ−12secθ.
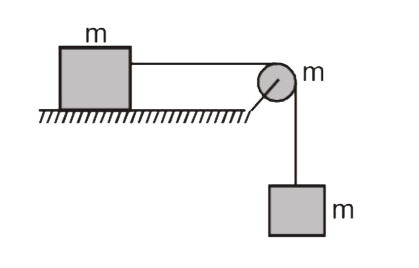
Figure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
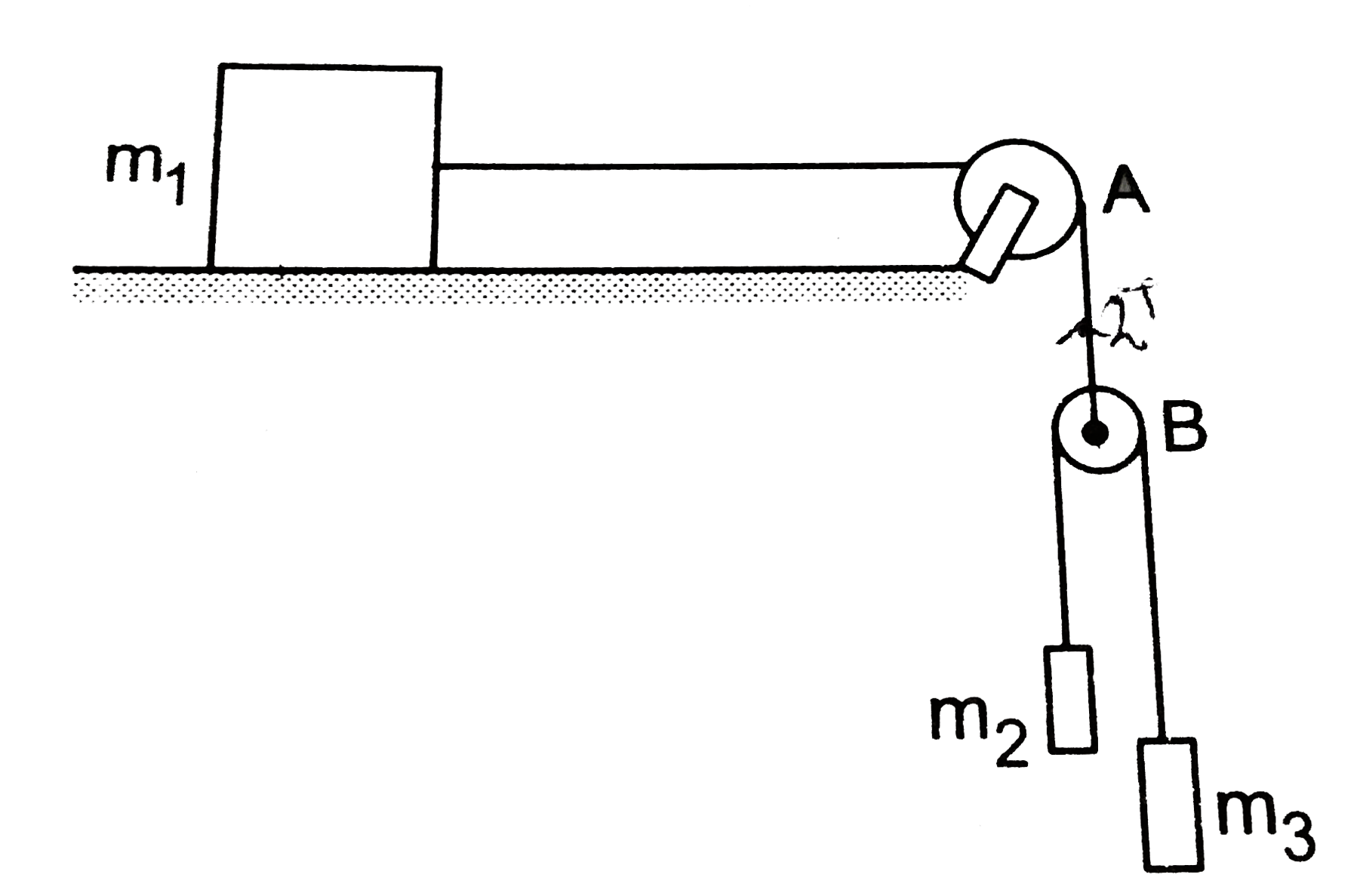
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1

View SolutionTwo bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
View SolutionTwo bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
View Solution
