A table with smooth horiztonal surface is truning at an angular speed ω abouyt its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have a table rotating with an angular speed ω. A particle is placed in a groove along the radius of the table at a distance a from the center. We need to find the speed of the particle when it moves to a distance L from the center.
Step 2: Identify Relevant Equations
The centripetal acceleration ac of the particle in circular motion is given by:
ac=ω2r
where r is the distance from the center. For our case, we can express this in terms of the speed v of the particle:
ac=v2r
Setting these two expressions for centripetal acceleration equal gives us:
v2r=ω2r
Step 3: Relate Speed and Distance
As the particle moves from distance a to L, we can express the relationship between speed and distance using the following differential equation:
vdvdx=ω2x
where x is the distance from the center.
Step 4: Integrate the Equation
We will integrate both sides. The left side integrates from 0 to v and the right side from a to L:
∫v0vdv=∫Laω2xdx
Calculating the left side:
v22∣∣∣v0=v22
Calculating the right side:
ω2∫Laxdx=ω2(x22∣∣∣La)=ω2(L2−a22)
Step 5: Set the Integrals Equal
Now we set the two results equal:
v22=ω2L2−a22
Step 6: Solve for v
Multiplying both sides by 2 gives:
v2=ω2(L2−a2)
Taking the square root yields:
v=√ω2(L2−a2)=ω√L2−a2
Final Answer
Thus, the speed of the particle when its distance from the center becomes L is:
v=ω√L2−a2
We have a table rotating with an angular speed ω. A particle is placed in a groove along the radius of the table at a distance a from the center. We need to find the speed of the particle when it moves to a distance L from the center.
The centripetal acceleration ac of the particle in circular motion is given by:
ac=ω2r
where r is the distance from the center. For our case, we can express this in terms of the speed v of the particle:
ac=v2r
Setting these two expressions for centripetal acceleration equal gives us:
v2r=ω2r
As the particle moves from distance a to L, we can express the relationship between speed and distance using the following differential equation:
vdvdx=ω2x
where x is the distance from the center.
We will integrate both sides. The left side integrates from 0 to v and the right side from a to L:
∫v0vdv=∫Laω2xdx
v22∣∣∣v0=v22
ω2∫Laxdx=ω2(x22∣∣∣La)=ω2(L2−a22)
Now we set the two results equal:
v22=ω2L2−a22
Multiplying both sides by 2 gives:
v2=ω2(L2−a2)
Taking the square root yields:
v=√ω2(L2−a2)=ω√L2−a2
Thus, the speed of the particle when its distance from the center becomes L is:
v=ω√L2−a2
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -1
16 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -2
6 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- FLUID MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions
90 Videos
Similar Questions
A table with smooth horizontal surface is turning at an angular speed ω about its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
View SolutionA table with smooth horizontal surface is turning at an angular speed ω about its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from the centre becomes L.
View Solution_S01_013_Q01.png)
A very small groove is made in the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle for that place.
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionA table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular pathof radius R. A smooth groove AB of length L(<<R) is made on the surface of the table. The groove makes an angleθ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along AB. Find the time taken by tehparticle to reach the point B.
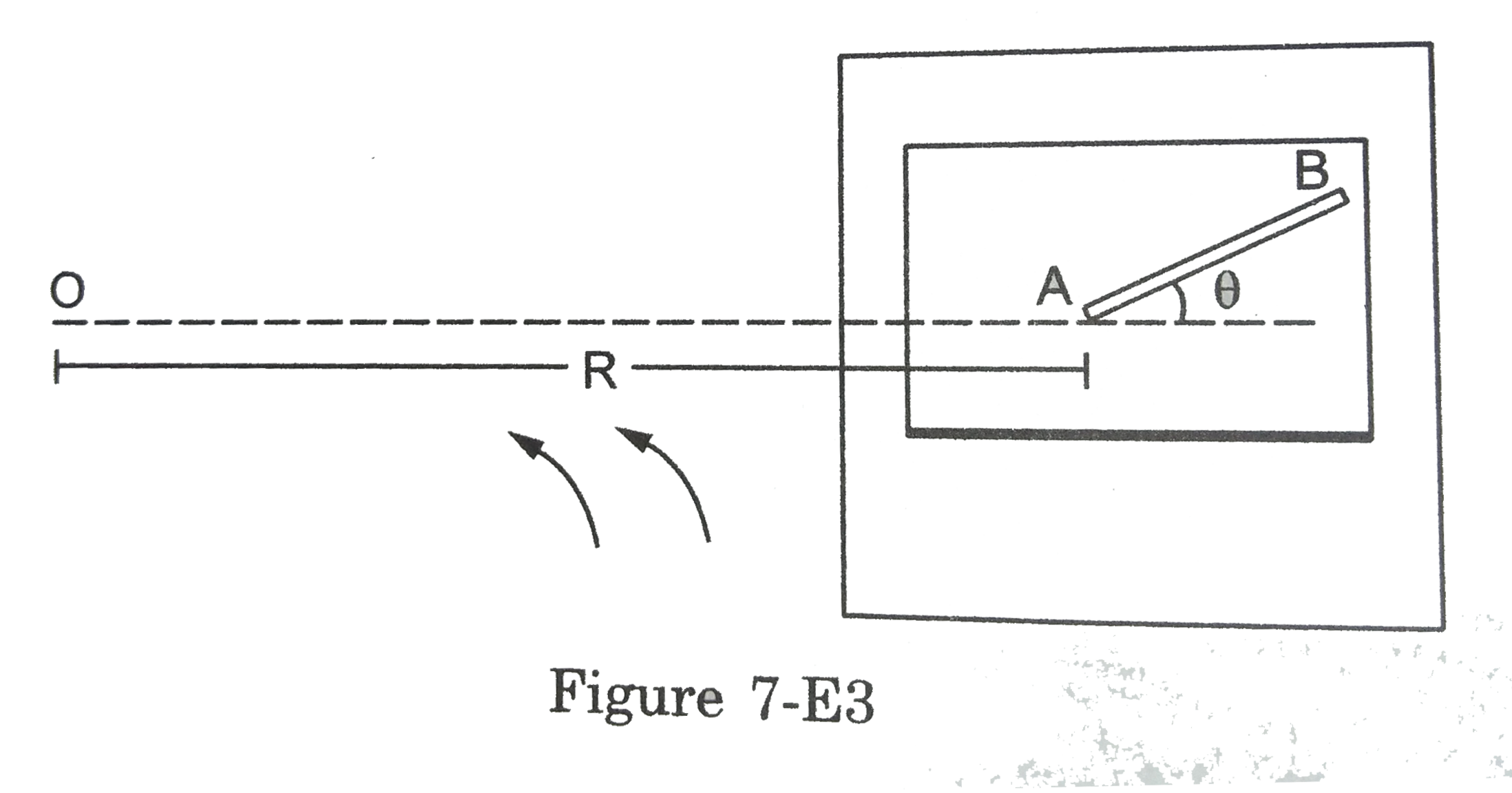
View SolutionA table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular pathof radius R. A smooth groove AB of length L(<<R) is made on the surface of the table. The groove makes an angleθ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along AB. Find the time taken by tehparticle to reach the point B.

View SolutionA positive charge q is placed in front of conducting solid cube at a distance d from its centre. Find the electric field at the centre of the cube due to the charges appearing on its surface.
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View Solution
