A thin converging lens is formed with one surface convex and the other plane. Does the position of image depend on whether the convex surface or the plane surface faces the object ?
To determine whether the position of the image formed by a thin converging lens depends on whether the convex surface or the plane surface faces the object, we can analyze the situation using the Lens Maker's formula.
1. Understand the Lens Maker's Formula:
The Lens Maker's formula is given by:
1f=(n−1)(1R1−1R2)
where:
- f is the focal length of the lens,
- n is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
2. Case 1: Convex Surface Facing the Object:
- Let the convex surface be R1 and the plane surface be R2.
- For the convex surface, R1=r (positive value) and for the plane surface, R2=∞ (since it is flat).
- Substituting these values into the Lens Maker's formula:
1f=(n−1)(1r−0)=n−1r
3. Case 2: Plane Surface Facing the Object:
- Now, let the plane surface be R1 and the convex surface be R2.
- For the plane surface, R1=∞ (flat surface, hence no curvature) and for the convex surface, R2=−r (negative because it is measured in the opposite direction).
- Substituting these values into the Lens Maker's formula:
1f=(n−1)(0−1r)=−n−1r
4. Comparing Both Cases:
- In the first case, we found f=rn−1.
- In the second case, we found f=−rn−1.
- The focal length changes sign depending on which surface is facing the object, but the magnitude remains the same.
5. Conclusion:
- The position of the image does depend on which surface of the lens is facing the object because the focal length changes sign. This indicates that the nature of the image (real or virtual) will also change depending on the orientation of the lens.
The Lens Maker's formula is given by:
1f=(n−1)(1R1−1R2)
where:
- f is the focal length of the lens,
- n is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
- Let the convex surface be R1 and the plane surface be R2.
- For the convex surface, R1=r (positive value) and for the plane surface, R2=∞ (since it is flat).
- Substituting these values into the Lens Maker's formula:
1f=(n−1)(1r−0)=n−1r
- Now, let the plane surface be R1 and the convex surface be R2.
- For the plane surface, R1=∞ (flat surface, hence no curvature) and for the convex surface, R2=−r (negative because it is measured in the opposite direction).
- Substituting these values into the Lens Maker's formula:
1f=(n−1)(0−1r)=−n−1r
- In the first case, we found f=rn−1.
- In the second case, we found f=−rn−1.
- The focal length changes sign depending on which surface is facing the object, but the magnitude remains the same.
- The position of the image does depend on which surface of the lens is facing the object because the focal length changes sign. This indicates that the nature of the image (real or virtual) will also change depending on the orientation of the lens.
Topper's Solved these Questions
Similar Questions
A plano-convex lens P and a concavo-convex lens Q are in contact as shown in figure. The refractive index o fthe material of the lens P and Q is 1.8and1.2 respectively. The radius of curvature of the concave surface of the lens Q is double the radius of curvature of the convex surface. The convex surface of Q is silvered.

An object is placed on the placed on the principal axis at a distance 10cm form the plane surface. The image is formed at a distance 40cm from the plane surfaces on the same side. The focal length of the system is
View SolutionBehind a thin converging lens having both the surfaces of the same radius 10cm, a plane mirror has been placed. The image of an object at a distance of 40 cm from the lens is formed at the same position. What is the refractive index of the lens?

View Solution
Knowledge Check
A bi-convex lens is formed with two thin plano-convex lenses as shown in the figure. Refractive index n of th efirst lens is 1.5 and that of the second lens if 1.2 Both the curved surfaces are of the same radius of curvature R=14cm. For this bi-convex lens, for an object distance of 40cm, the image distance will be
 A−280.0cmB40.0cmC21.5cmD13.3cm
A−280.0cmB40.0cmC21.5cmD13.3cm
An unsymmeterical double convex thin lens forms the image of a point object on its axis. Will the position of the image change if the lens is reversed ?
View SolutionA plano-convex lens P and a concavo-convex lens Q are in contact as shown in figure. The refractive index o fthe material of the lens P and Q is 1.8and1.2 respectively. The radius of curvature of the concave surface of the lens Q is double the radius of curvature of the convex surface. The convex surface of Q is silvered.The focal lengthof combination is 8cm. The radius of curvature of common surface is
View SolutionA thin convex lens from a real Image of a certain object 'p' times it size .The size of real image become 'q' times that of object when the lens is moved nearer to the object by a distance 'a' find focal length of the lens?
View SolutionFind the refractive index of the material of a plano-convex lens, if the radius of curvature of the convex surface is 20 cm and focal length of the lens is 60 cm?
View SolutionThe image for the converging beam after refraction through the curved surface is formed at
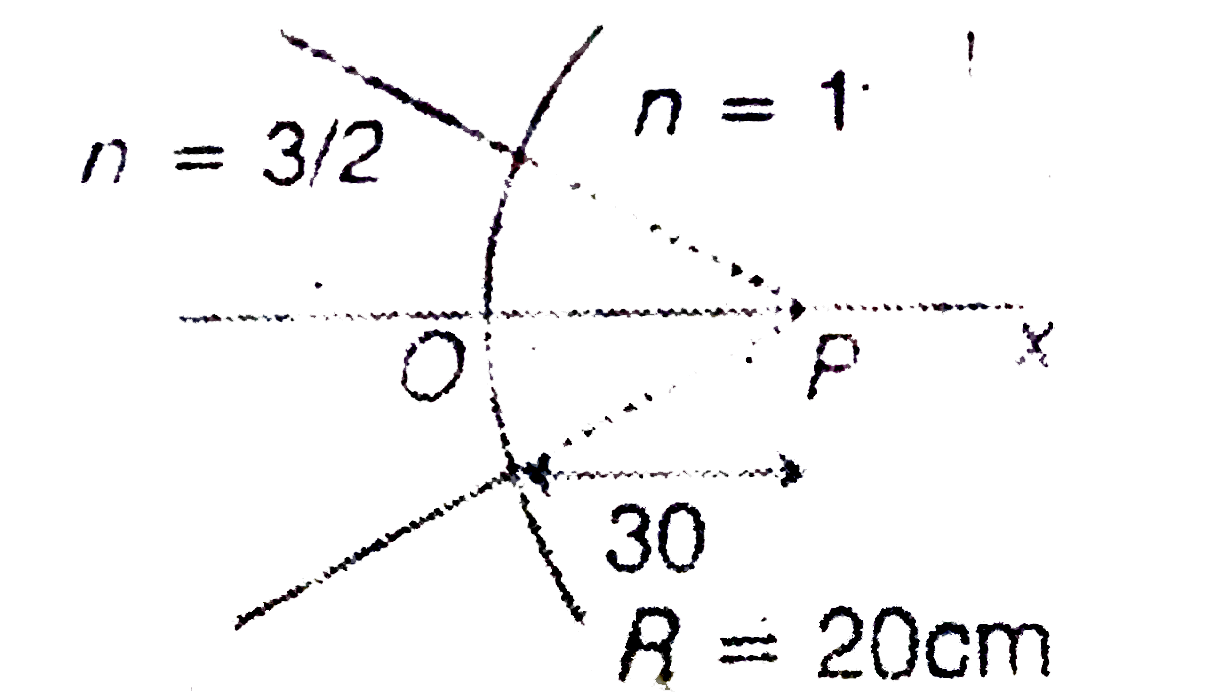
View SolutionThe image for the converging beam after refraction through the curved surface is formed at
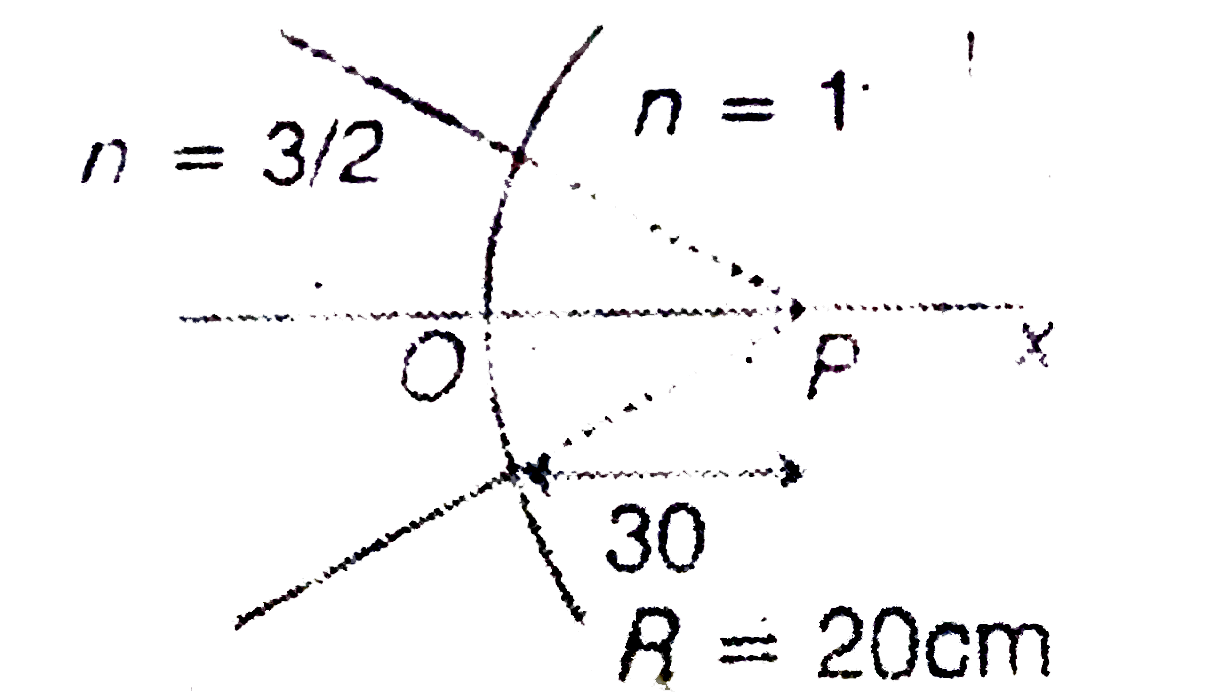
View SolutionPlane surface of a thin plano-convex lens is silvered. If a point object is placed on principal axis at a distance 60cm from the lens and fial image is formed at a distance 30cm from the lens on same side. What will be the distance of final imagge from the lens if the plane surface is not silvered.
View Solution
