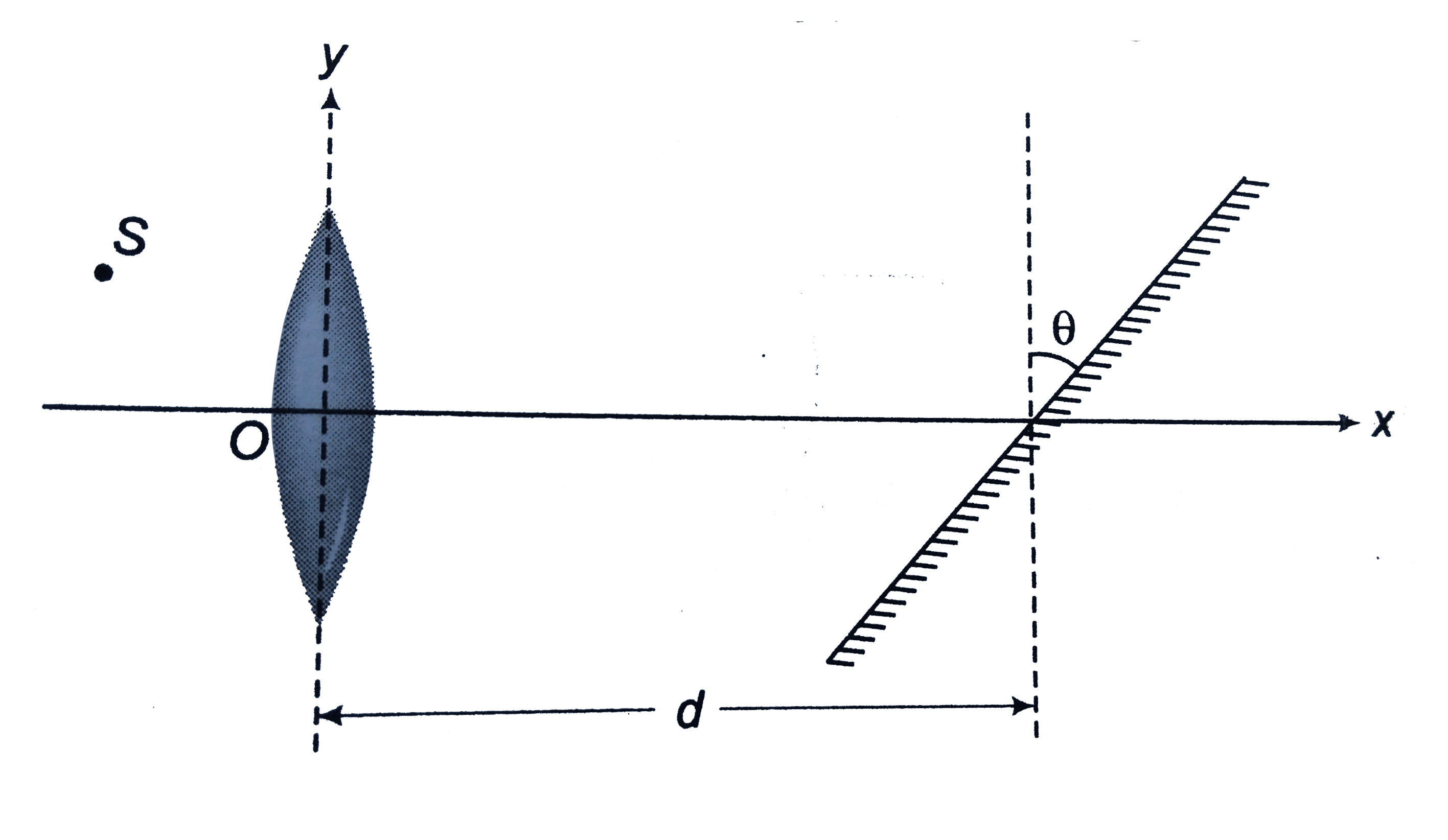
A thin converging lens of focal length f=1.5m is placed along y-axis such that its optical centre coincides with the origin. A small light source S is placed at (−2.0m,0.1m). Where should a plane mirror inclined at an angle θ,tanθ=0.3 be placed such that y-coordinate of final image is 0.3m, i.e. find d. Also find x-coordinate of final image.
The correct Answer is:5
1v−1u=1f
1v−1−2=11.5,v=6m
m=vu=−3
x=6−d,
tanθ=0.3x
⇒d=5m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives7videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - True/False5videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension51videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
Two thin equiconvex lenses each of focal length 0.2 m are placed coaxially with their optic centres 0.5m apart. Then find the focal length of the combination.
View SolutionA convex lens of focal length 1.5m is placed in a system of coordinate axis such that its optical centre is at origin and principa, axis coinciding with the x-axis. An object and a plane mirror are arrange on theh principal axis as shown in figure. Find value of d (in m) so that y-coordinate of image (after refraction and reflection ) is 0.3m. (Take tanθ=0.3)
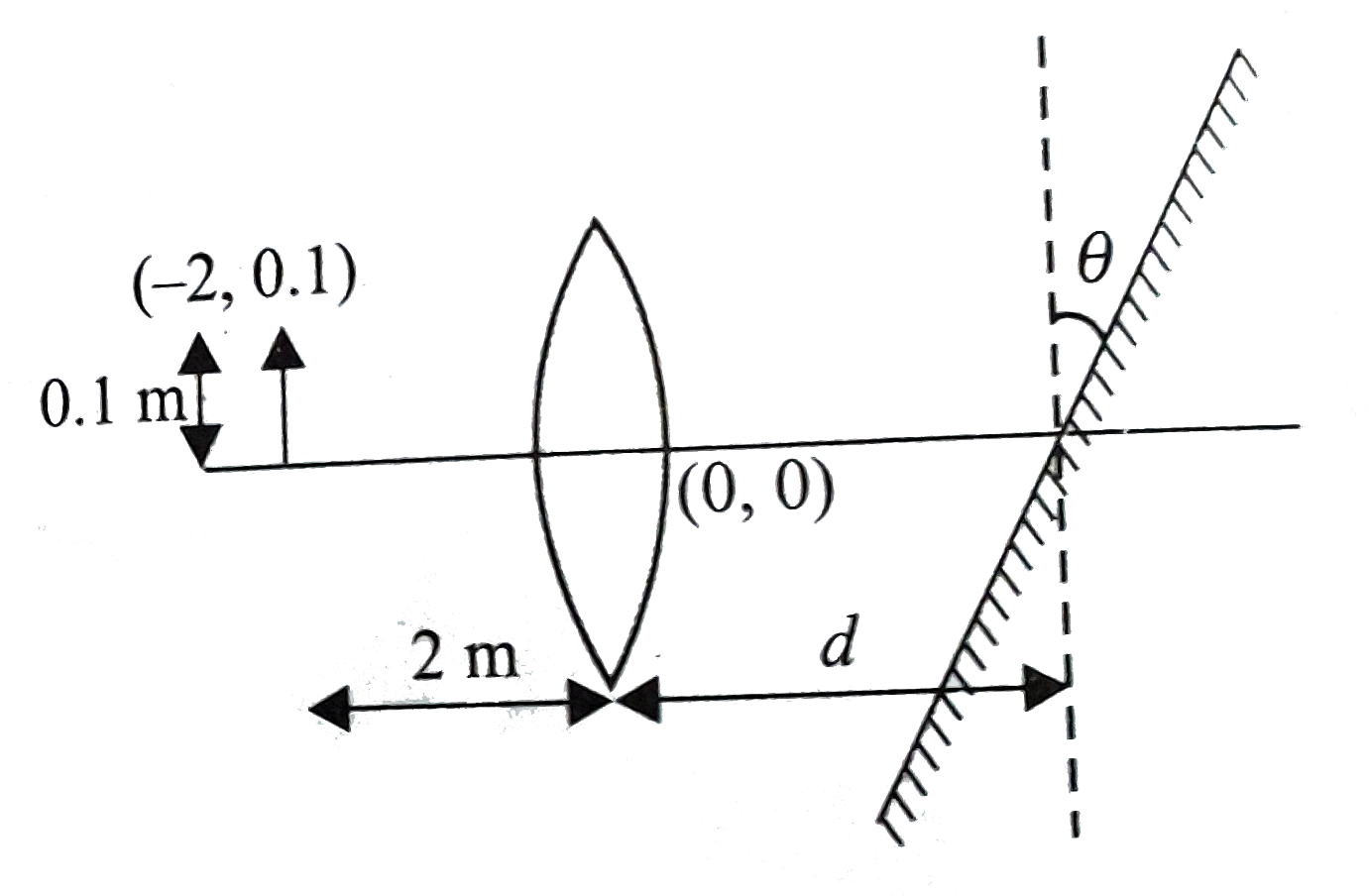 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A thin convex lens of focal length 25cm is cut into two pieces 0.5cm above the principal axis. The top part is placed at (0,0) and an object placed at (−50cm,0). Find the coordinates of the image.
A(50cm,−2cm)B(50cm,−1cm)C(3cm,−50cm)D(60cm,−25cm)
A thin convex lens of focal length 25cm is cut into two pieces 0.5cm above the principal axis. The top part is placed at (0,0) and an object placed at (−50cm,0). Find the coordinates of the image.
View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart. If a pin of length 2.0 cm is placed 30 cm from the lens farther away from the mirror, where will the final image form and what will be the size of the final image ?
View SolutionA converging lens has a focal length of 0.12 m. To get an image of unit magnification the object should be placed at what distance from the converging lens ?
View SolutionA converging lens of focal length 12 cm and a diverging mirror of focal length 7.5 cm are placed 5.0 cm apart with their principal axes coinciding. Where should an object be placed so that its image falls on itself ?
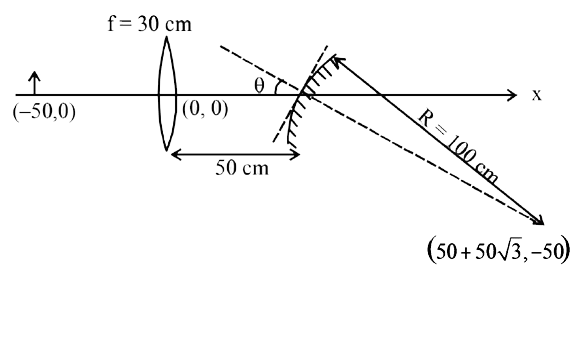
View SolutionA small object is placed 50 cm to the left of a thin convex lens of focal length 30 cm. A convex spherical mirror of radius of curvature 100 cm is placed to the right of the lens at a distance of 50 cm. The mirror is tilted such that the axis of the mirror is at an angle θ=30degree to the axis of the lens, as shown in the figure
If the origin of the coordinate system is taken to be at the centre of the lens, the coordinates (in cm) of the point (x,y) at which the image is formed are
 View Solution
View SolutionA thin biconvex lens of refractive index 3/2 and radius of curvature 50cm is placed on a reflecting convex surface of radius of curvature 100cm. A point object is placed on the principal axis of the system such that its final image coincides with itself. Now, few drops of a transparent liquid is placed between the mirror and lens such that final image of the object is at infinity. Find refractive index of the liquid used. Also, find the position of the object.
View SolutionA converging lens of focal length 15 cm and a converging mirror of focal length 20 cm are placed with their principal axes coinciding. A point source S is placed on the principal axis at a distance of 12 cm from the lens as shown in figure. It is found that the final beam comes out parallel to the principal axis. Find the separation between the mirror and the lens.
 View Solution
View Solution
