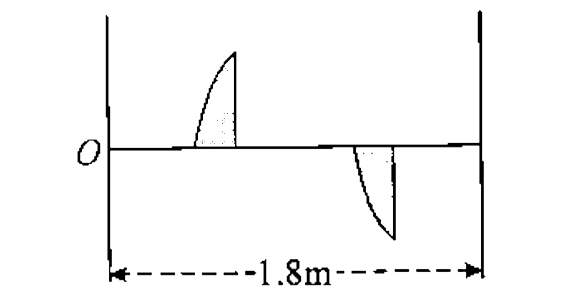
A thin plano-convex lens of focal length f is split into two halves. One of the halves is shifted along the optical axis as shown in figure. The separation between object and image planes is 1.8 m. The magnification of the image, formed by one of the ball lens is 2. Find the focal length of the lens and separation between the two halves. Draw the ray diagram for image formation.
The correct Answer is:D
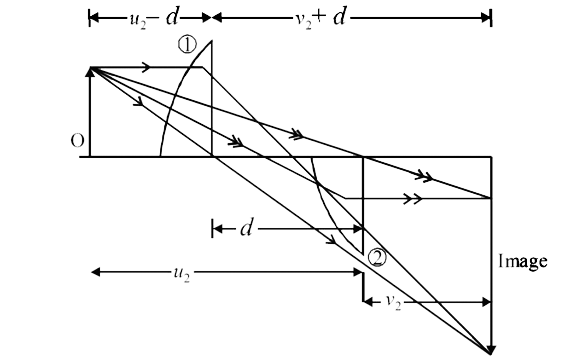
Given …(i)
The magnification of lens (1) is 2
….(ii)
From (i) and (ii)
,v_2=1.2-d(1)/(v_2+d)+(1)/(u_2-d)=(1)/(f)(1)/(v_2)+(1)/(u_2)=(1)/(f)(1)/(v_2+d)+(1)/(u_2-d)=(1)/(v_2)+(1)/(u_2)implies(1)/(1.2-d+d)+(1)/(0.6+d-d)=(1)/(1.2-d)+(1)/(0.6+d)impliesd=0.6m(1)/(1.2-0.6)+(1)/(0.6+0.6)=(1)/(f):'f=0.4m
Topper's Solved these Questions
Similar Questions
A thin plano-convex lens.of focal length f is split into two halves : One of the halves is shifted along the optical axis (figure)The separation between object and image planes is 1.8m.The magnification of the image formed by one of the half lensis 2. Find the focal length of the lens and separation between the two halves. Draw the ray diagram for image formation.
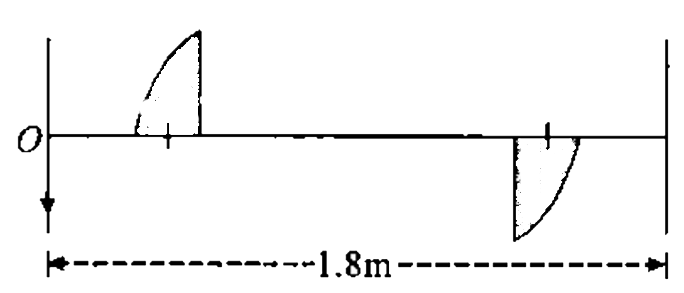
View SolutionA thin plano-convex lens of focal length f is split into two halves. One of the halves is shifted along the optical axis as shown in figure. The separation between object and image planes is 1.8 m. The magnification of the image, formed by one of the ball lens is 2. Find the focal length of the lens and separation between the two halves. Draw the ray diagram for image formation.

View Solution
Knowledge Check
If a equiconvex lens of focal length f is cut into two halves by a plane perpendicular to the principal axis, then
AThe focal length of each half becomesf2BThe focal length of each half becomes 2fCThe focal length of each half remains fDThe focal length of each half becomes f4The distance between an object and its real image formed by a lens is D. If the magnification is m, the focal length of the lens is
A(m−1)DmBmD(m+1)C(m−1)Dm2DmD(m+1)2Shown an object and its image formed by a thin lens. Then the nature and focal length of lens is
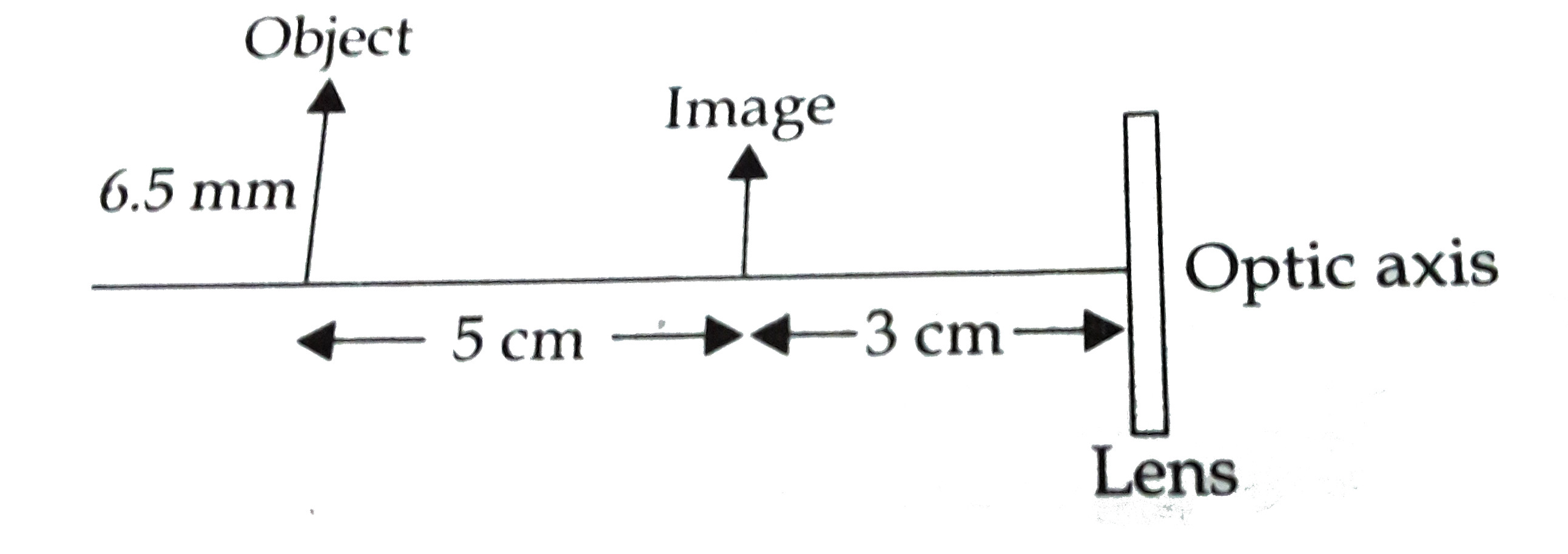 Af=4.8cm converging lensBf=−4.8cm diverging lensCf=2.18cm converging lensDf=−2.18cm diverging lens
Af=4.8cm converging lensBf=−4.8cm diverging lensCf=2.18cm converging lensDf=−2.18cm diverging lens
A thin plano-convex lens of focal length f is split into two halves. One of the halves is shifted along the optical axis as shown in figure. The separation between object and image planes is 1.8 m. The magnification of the image, formed by one of the ball lens is 2. Find the focal length of the lens and separation between the two halves. Draw the ray diagram for image formation.

View SolutionA thin double convex lens of focal length f is broken into two equal halves at the axis. The two halves are combined as shown in figure. What is the focal length of combination in (ii) and (iii).
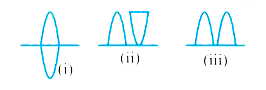
View SolutionThe distance between the object and the real image formed by a convex lens is d. If the linear magnification is m, find the focal length of the lens in terms of d and m.
View SolutionDraw ray diagram showing the image formation by a convex lens when an object is placed at twice the focal length of the lens.
View SolutionA cocave lens forms the image of an object such that the distance between the object and image is 10 cm and the magnification produced is 1/4. the focal length of the lens will be
View Solution
