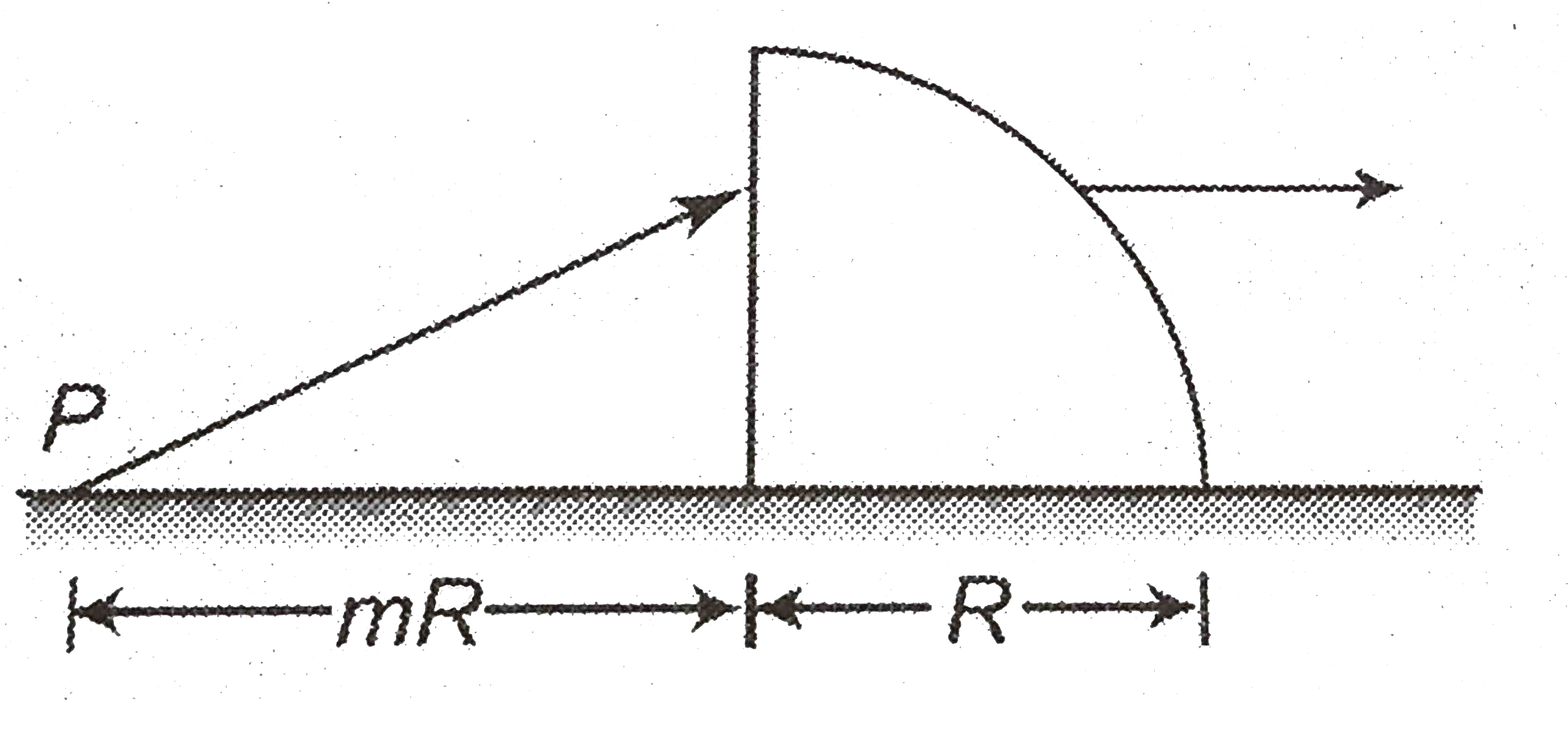
A quarter cylinder of radius R and refractive index 1.5 is placed on a table.A point object P is kept at a distance of mR from it. Find the value of m for whicha ray from P will emerge parallel to the table as shown in the figure.
The correct Answer is:C, D
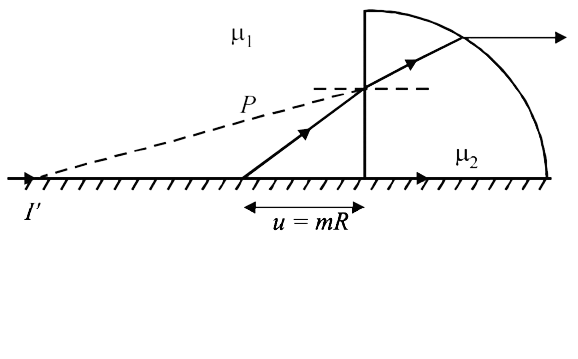
First of all, we consider the refraction the refraction at plane surface. Here the image of P will from I)afterretionomIsurface.<br>Forpla≠surface:<br>Objectdistanceu=-mR<br>Radiusofcurvatureofthepla≠surface=infty<br>Therayiscomingomairand∈cntontheglass.<br>Heremu_(1)=1,mu_(2)=1.5<br>Applymu_(2)/(v)-(mu_(1))/(u)=(mu_(2)-mu_(1))/(R),(mu_(2))/(v)=(mu_(1))/(u)...(as R=infty)<br>:'Ima≥distancev=(mu_(1))/(mu_(2))u=(1.5)/(1.0)(-mR)=-1.5mR<br>Nowweconsrretionatthecurvedsurface.Objectdistance,u=-(1.5mR+R)<br>Here,mu_(2)=1,μ1=1.5, Image distance, v=∞,
Radius of curvature=−R
Here, 1∞+1.5(1.5m+1)R=1−1.5−R ∵ m=43
Topper's Solved these Questions
Similar Questions
A point object is kept at a distance of 2m from origin on x− axis. A quarter cylinder of radius R=30 cm and refractive index μ=1.5 having its axis ⊥r to plane of paper is placed between the object and the parabolic reflector at a distance of 130cm from origin as shown in figure. The position of the image after reflection from the parabolic reflector y2=2x is 25λcm. Find the value of λ?

View SolutionA hemisphere of radius R, made of glass of refractive index (3/2) is placed on 'the table. A point source of light is placed at a distance 2R from the centre, of hemisphere. If source is viewed diametrically opposite side of hemisphere. Find the position of image of source.

View Solution
Knowledge Check
A glass hemisphere of radius R and of material having refractive index 1.5 is silvered on its flat face as shown in figure., A small object of height h is located at a distance 2R from the surface of hemisphere as shown in the figure. The final image will form.
 Aat a distance of Rfrom silvered surface, on the right side.Bon the object itselfCat hemispher surfaceDat a distance of 2R from the silvered surface, on left side
Aat a distance of Rfrom silvered surface, on the right side.Bon the object itselfCat hemispher surfaceDat a distance of 2R from the silvered surface, on left sideAn object is placed in front of a sphere of radius R at a distance x from the first surface. The value of x for which the light after refraction from the first surface becomes parallel to the axis is
ARμ−1BRμ+1C2R1+μDRμμ+1A light ray from an object 'P' is reflected from a mirror as shown in the figure, then
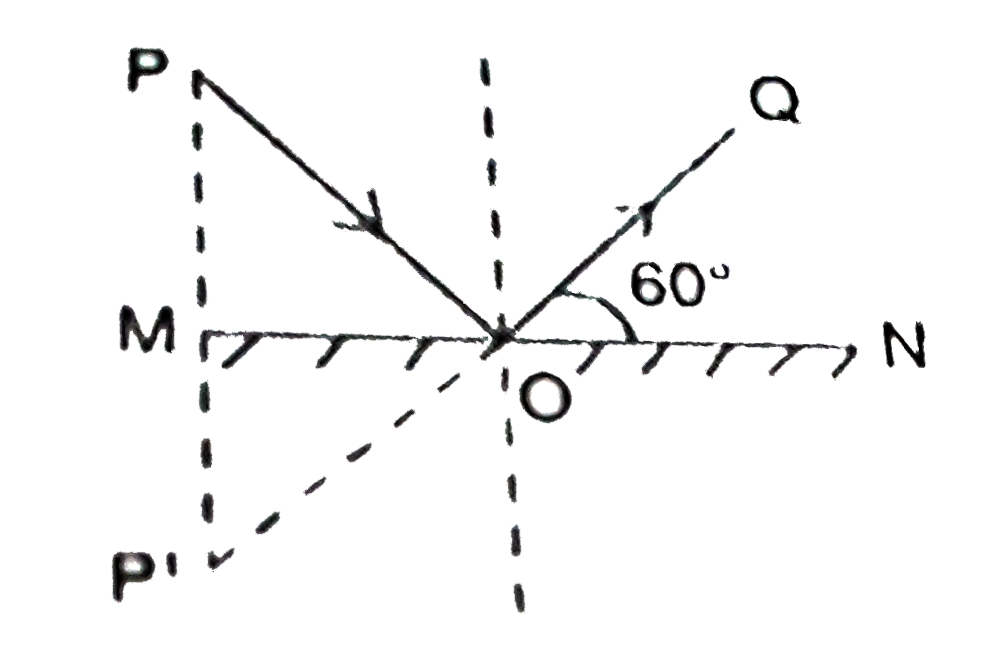 Aangle of incidence isBPM=MP1C∠PON=120∘DAll of the above
Aangle of incidence isBPM=MP1C∠PON=120∘DAll of the above
A double convex spherical glass has refractive index 1.5 and both radius of curvature 30 cm. A point object is placed at a distance of 120 cm from the spherical glass. What will be the position of the image formed ?
View SolutionA light ray from an object 'P' is reflected from a mirror as shown in the figure, then

View SolutionThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
 if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given by
if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given by
View SolutionA hemishperical surface of radius R and refractive index μ=1.5 is polished as shown. At what distance x from point P a point object O be placed so that its image coincides with the object itself?

View SolutionThere is a sphere of radius R and refractive index μ. At what distance from the surface of sphere should an object be placed so that real image is formed at the same distance from the sphere ?
View Solution
