The XY plane is the boundary between two tranparednt media. Medium 1 with z≥0 has a refraxtive index of √2 and medium 2 with z≤0 has a refractive index of √3. A ray of light in medium 1 given by the vector 6√3ˆi+8√3ˆj−10ˆk is incident on teh plane of separation. Find the unit vector in the direction of teh refracted ray in medium 2.
The correct Answer is:A, B, C, D
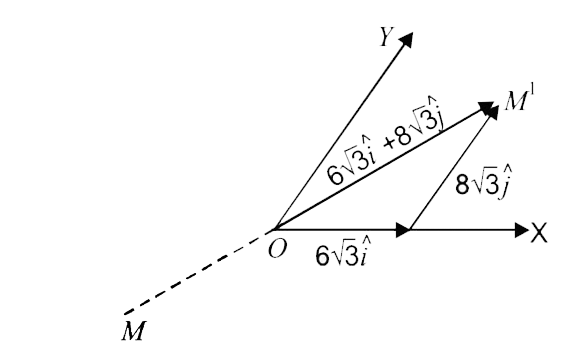
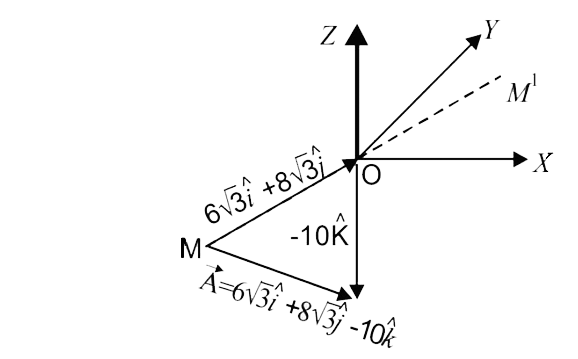
Figure 1 shows vector OM^==6sqrt3i+8sqrt3hatj<br>Figure2shows→−−→rvecA=6sqrt3hati+8sqrt3hatj-10hatk<br>Theperpendica––r→l∈eMOM^ is Z-axis which has a unit vector of ˆk.
Angle between vextor vec(MP)andvec(OP)canbefoundby.∏uct.vec(MP),vec(OP)=(MP)(OP) cosi<br>((6sqrt3hati+8sqrt3hatj-10hatk).(-hatk))/(sqrt((6sqrt3)^(2)+(8sqrt3)^(2)+(-10)^(2)+sqrt((-1)^(2))))=cosiimpliesi=60circ<br>Unit→−−→r∈thefirectionofMOM^() from fig. (1) is
ˆn=6√3ˆi+8√ˆj[(6√3)2+(8√3)2]12),hatn=(3)/(5)hati+(4)/(5)hatj<br>Tof∈dthe∠ofretion,weuseS≠ll'slaw<br>(sqrt3)/(sqrt2)=(sini)/(sinr)=(sin60^circ)/(sinr)implies45^circ<br>Now,hatr=(sinr)hatn-(cosr)hatk<br>=(sin45^circ)[(3)/(5)hati+(4)/(5)hatj]-(cos45^circ)hatk<br>=(1)/(5sqrt2)[3hati+4hatj-5hatk]
Topper's Solved these Questions
Similar Questions
Let the x-z plane be the boundary between two transparent media. Medium 1 in z≥0 has a refractive index of √2 and medium 2 with z<0 has a refractive index of √3. A ray of light in medium 1 given by the vector →A=6√3ˆi+8√3ˆj−10ˆk is incident on the plane of separation. The angle of refraction in medium 2 is:
View SolutionThe x−y plane is the boundary between two transparent media. Medium-1 with z>0 has refractive index √2 and medium −2 with z<0 has a refractive index √3. A ray of light in medium −1 given by the vector A=6√3i+8√3j−10k is incident on the plane of separation. If the unit vector in the direction of refracted ray in medium −2 is 15(ai+bj−5√2k) then the value of ab.
View Solution
Knowledge Check
Let the x-z plane be the boundary between two transparent media. Medium 1 in z≥0 has a refractive index of √2 and medium 2 with z<0 has a refractive index of √3. A ray of light in medium 1 given by the vector →A=6√3ˆi+8√3ˆj−10ˆk is incident on the plane of separation. The angle of refraction in medium 2 is:
A45∘B60∘C74∘D30∘Let the x-z plane be the boundary between two transparent media. Media 1 in z≥0 has refractive index of √2 and medium 2 with z<0 has a refractive index of √3. A ray of light in medium 1 given by the vector →A=6√3ˆi+8√3ˆj−10ˆk in incident on the plane of separation. The angle of refraction in medium 2 is
A30∘B45∘C60∘D75∘Let the x-z plane be the boundary between two transparent media . Medium 1 in z≤0 has a refrative index of √2 and medium 2 with z<0 has a refracticve index of √3 A ray of light in medium 1 given by the vector →A=6√3ˆi+8√8ˆj−10ˆk is incident on the plane of separation . The angle of refraction in medium 2 is
A40∘B60∘C75∘D30∘
[" The "xz" plane is the boundary "],[" between two transparent medium."],[" Medium - I with "y>=0" has "],[" refractive index "mu" and medium - II "],[" with "y<=0" has a refractive index 1."],[" A ray of light in medium-I,given by "],[" vector "vec n=hat i-sqrt(3)hat j" is incident on "],[" the plane of separation.If the "],[" reflected and refracted rays make "],[" an angle of "90^(@)" with each other,"],[" then the value of "mu" is "sqrt(k)" .Find the "],[" value of "k" ."]
View SolutionTwo plane mirrors are combined to each other as such one is in (y-z) plane and other is in (x-z)plane.A ray of light along vector 1√3ˆi+1√3ˆj+1√3ˆk is incident on the first mirror. Find the unit vector in the direction of emergence ray after successive reflections through these mirros.
View Solutionx-y plane separates two media, z≥0 contains a medium of refractive index 1 and z≤0 contains a medium of refractive index 2. A ray of light is incident from first medium along a vectorˆi+ˆj−ˆk. Find the unit vector along the refracted ray.
View SolutionThe x−y plane is the boundary between two transparent media. Medium-1 with z≤0 has a refractive index √2 and medium -2 with z≤0 has a refractive index √2. A ray of light in medium -1 given by vector A=√3ˆi−ˆk is incident on the plane of separation. The unit vector in the direction of the refracted ray in medium-2 is
View SolutionA ray of light is incident on a medium of refractive index √2 at an angle of incidence of 45∘. The ratio of the width of the incident beam in air to that of the refracted beam in the medium is
View Solution
