A vessel ABCD of 10cm width has two small slits S1 and S2 sealed with idebtical glass plates of equal thickness. The distance between the slits is 0.8mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S,40cm below P and 2m from the vessel, to illuminate the slits as shown in the figure. Calculate the position of the central bright fringe on the other wall CD with respect of the line OQ. Now, a liquid is poured into the vessel and filled up to OQ. The central bright fringe is fiund to be at Q. Calculate the refractive index of the liquid.

The correct Answer is:A, B, C
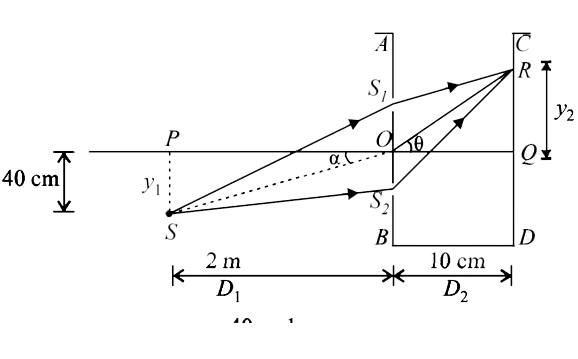
(i) O is the middle point of two slits S−1 and S2.
S1S2=d=0.8mm
tanα+y1D1=40200=15
∵ sinα=1√26=15.1≈11.5≈tanα
Path defference △X1=SS1−SS2
or △X1=dsinα=(0.8mm)(15)=0.16mm...(i)
Let R denotes the position of central bright fringe. Net path defference will be zero.
Now △X2=S2R−S1R or △X2=dsinθ...(ii)
For central bright fringe
△X2−△X1=0 or dsinθ−△X1=0
or dsinθ=0.16 or sinθ=0.160.8=15 ∵ tanθ=1√24=14.9≈15=sinθ ∵tanθ=y2D2
or 15=y2D2 or y2=D25=105=2cm
Hence position of central bright fringe is 2 cm above point Q on side CD.
(ii) μ of liquid poured if central fringe is at Q:
The liquid is poured into vessel upto OQ.
The central bright fringe is formed at Q.
For central bright fringe net path defference=0
(μ−1)t=△X1 or (μ−1)(100)=0.16
or μ−1=0.0016 or μ=1.0016

Topper's Solved these Questions
Similar Questions
A vessel ABCD of 10 cm width has two small slits s1 and S2 sealed, with identical glass plates of equal thickness. The distance between the slits is 0.8. mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept al S. 40 cm below P and 2m from the vessel, to illuminate the slits as shown in the figure below. 40cm Calculate the position of the central bright fringe on the other wall CD with respect to the line OQ. Now, a liquid is poured into the vessel and filled up to-OQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid

View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S1 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View Solution
Knowledge Check
In Young's double slit experiment, the distance between the two slits is 0.1 mm, the distance between the screen and the slit is 100 cm. if the width of the fringe is 5 mm, then the wavelength of monochromatic light used is
A4000 ÅB6000 ÅC5000 ÅD5400 ÅIn a Young’s double slit experiment, the source illuminating the slits is changed from blue to violet. The width of the fringes
AIncreasesBDecreasesCBecomes unequalDRemains constantIn the given figure ,C is middle point of line S1S2.A monochromatic light of wavelength γ is incident on slits.The ratio of intensites of S3andS4 is
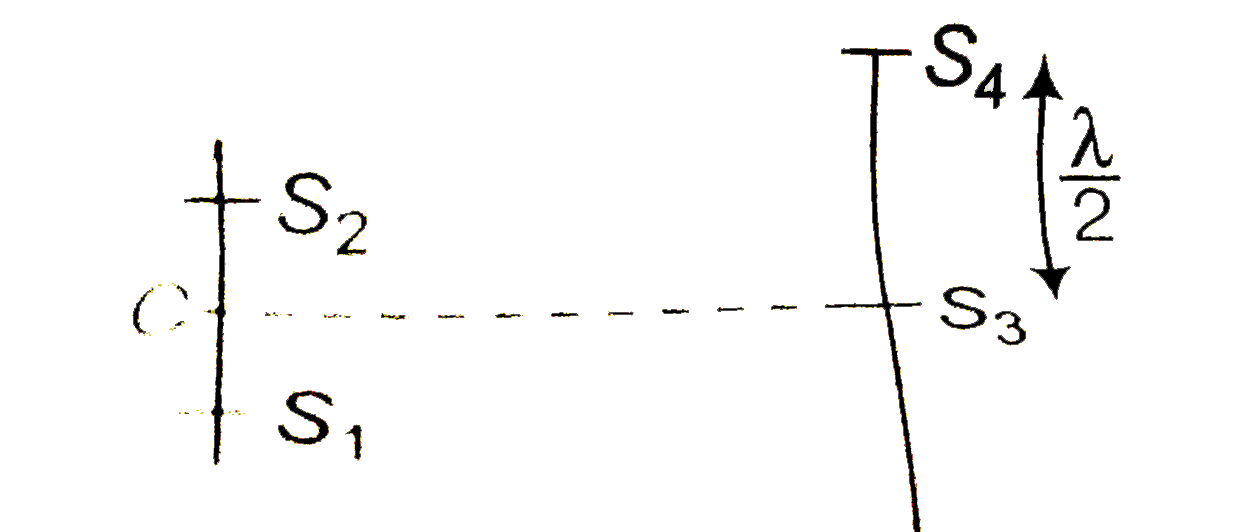 A0B∞C4:1D1:4
A0B∞C4:1D1:4
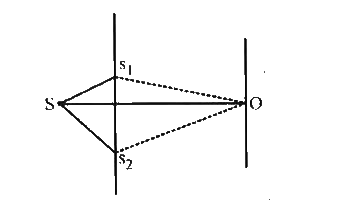
In an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
View SolutionIn an interference experiment , two parallel verticals slits S1 and S2 are used. A thin glass plate is introduced in the path of light from S1. Then
View SolutionA coherent light is incident on two paralle slits S1andS2. At a point P1 the frings will be dark if the phase difference between the rays coming from S1andS2 is
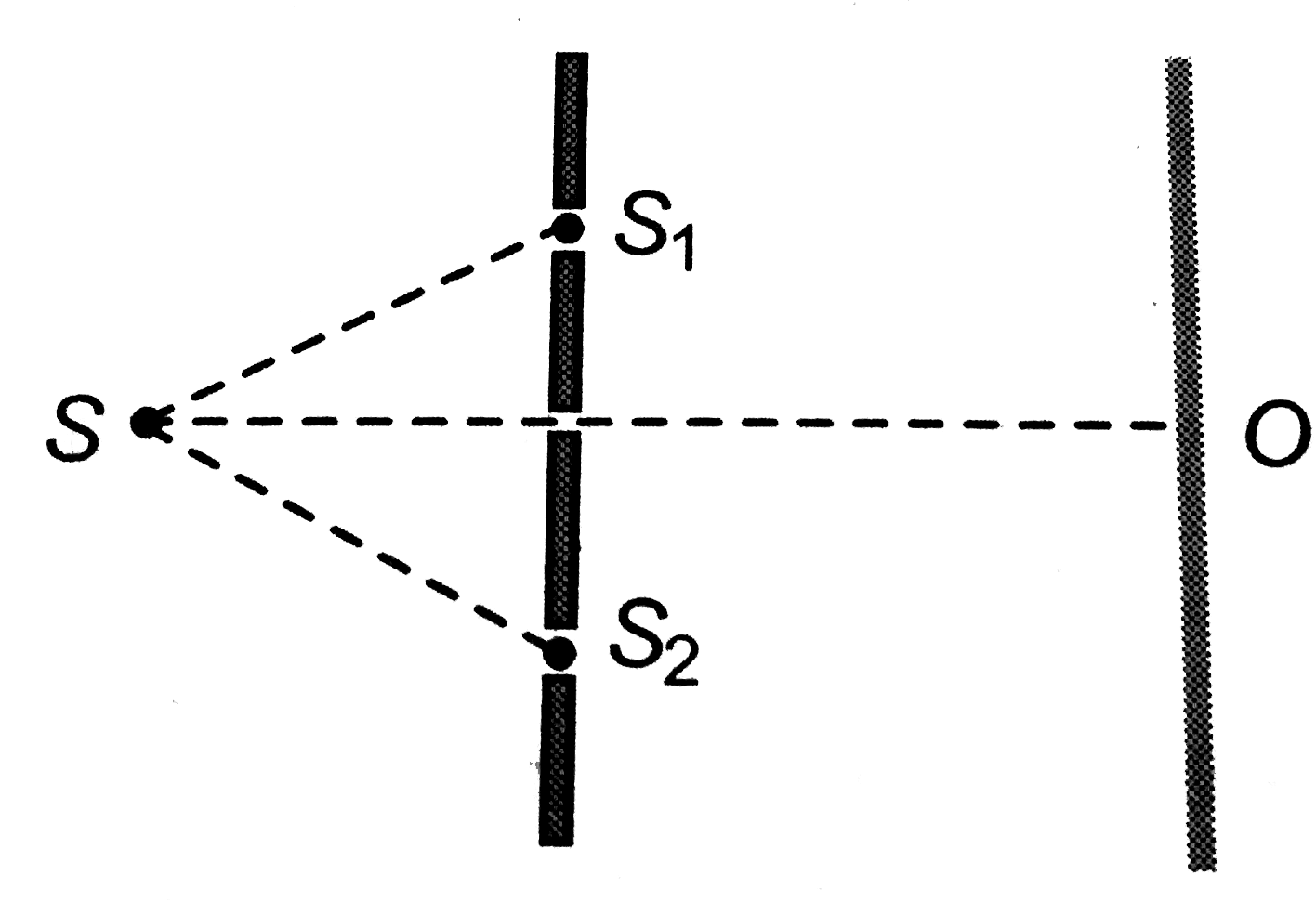
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
View SolutionIn Young’s experiment, monochromatic light through a single slit S is used to illuminate the two slits S1and S2. Interference fringes are obtained on a screen. The fringe width is found to be w. Now a thin sheet of mica (thickness t and refractive index μ) is placed near and in front of one of the two slits. Now the fringe width is found to be w’, then :
View Solution
