A transverse wave is tranvelling in a string at any moment a small element 'dx' is at inclination 30∘ with the direction of propagation of the wave. After some time interval its inclination changes to 60∘ with direction of propagation. Potential energy of this small element is initially U0 and finally it is KU0, value of K is
2
9
3
4
The correct Answer is:B
To solve the problem, we need to analyze the relationship between the potential energy of a small element of the string and its angle of inclination with the direction of wave propagation.
1. Understanding Potential Energy in Transverse Waves:
The potential energy (U) of a small element of the string in a transverse wave is directly proportional to the square of the sine of the angle (θ) that the element makes with the direction of wave propagation. This can be expressed mathematically as:
U∝sin2(θ)
2. Initial Condition:
Initially, the angle of inclination is 30∘. Therefore, the initial potential energy U0 can be expressed as:
U0=k1sin2(30∘)
where k1 is a proportionality constant. We know that:
sin(30∘)=12
Thus,
U0=k1(12)2=k1⋅14
3. Final Condition:
After some time, the angle changes to 60∘. The final potential energy KU0 can be expressed as:
KU0=k2sin2(60∘)
where k2 is another proportionality constant. We know that:
sin(60∘)=√32
Thus,
KU0=k2(√32)2=k2⋅34
4. Relating Initial and Final Potential Energies:
Since we have U0 and KU0, we can set up the following relationship:
KU0=34k2
and
U0=14k1
5. Finding the Value of K:
We can express the ratio of the two potential energies:
U0KU0=14k134k2
Simplifying this gives:
1K=13
Therefore, we can find K:
K=3
Final Answer:
The value of K is 3.
---
The potential energy (U) of a small element of the string in a transverse wave is directly proportional to the square of the sine of the angle (θ) that the element makes with the direction of wave propagation. This can be expressed mathematically as:
U∝sin2(θ)
Initially, the angle of inclination is 30∘. Therefore, the initial potential energy U0 can be expressed as:
U0=k1sin2(30∘)
where k1 is a proportionality constant. We know that:
sin(30∘)=12
Thus,
U0=k1(12)2=k1⋅14
After some time, the angle changes to 60∘. The final potential energy KU0 can be expressed as:
KU0=k2sin2(60∘)
where k2 is another proportionality constant. We know that:
sin(60∘)=√32
Thus,
KU0=k2(√32)2=k2⋅34
Since we have U0 and KU0, we can set up the following relationship:
KU0=34k2
and
U0=14k1
We can express the ratio of the two potential energies:
U0KU0=14k134k2
Simplifying this gives:
1K=13
Therefore, we can find K:
K=3
The value of K is 3.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-II (LEVEL-II(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))4videos
WAVE MOTION
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-II (LEVEL-II(ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))4videos
WAVE MOTION
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-II (LEVEL-I(MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))4videos
WAVE MOTION
- BOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -366videos
UNITS AND MEASUREMENTS
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)97videos
WAVE MOTION AND SOUND
Similar Questions
A transverse wave of amplitude 0.5m and wavelength 1 m and frequency 2 Hz is propagating in a string in the negative x - direction. The expression for this wave is [
View SolutionA particle of mass is moving in a straight line with momentum p. Starting at time t= 0, a force F= kt acts in the same direction on the moving particle during time interval T so that its momentum changes from p to 3p. Here k is constant . The value of T is :
View SolutionA transverse wave propagating on a stretched string of linear density 3×10−4kg−m−1 is represented by the equation
y=0.2sin(1.5x+60t)
Where x is in metre and t is in second. The tension in the string (in Newton) isView SolutionHuygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
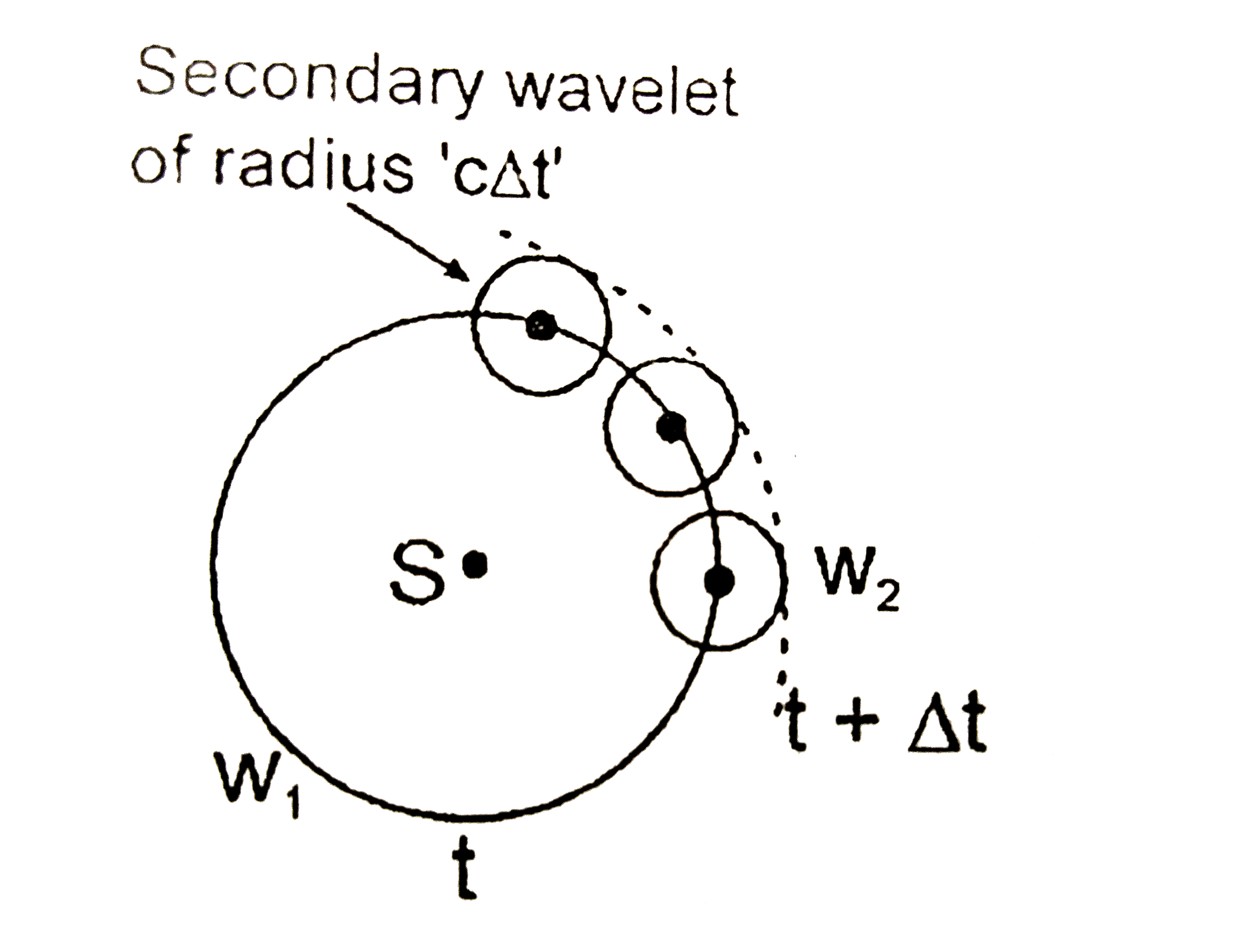
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)View SolutionA transverse harmonic wave on a string is described by y(x,t)=3.0sin(36t+0.018x+π/4) where x, y are in cm, t in second. The positive direction of x is from left to right . (i) Is this a travelling or stationary wave ? If travellying, what are the speed and direction of its propagation ? (ii) what are its amplitude and frequency ? (iii) what is the inital phase at the origing ? (iv) What is the least distance between two successive creests in the wave?
View SolutionA transverse wave is propagating along +x direction. At t=2 sec the particle at x=4m is at y=2 mm. With the passage of time its y coordinate increases and reaches to a maximum of 4 mm. The wave equation is (using ω and k with their usual meanings)
View SolutionStatement-1 : Standing wave of small amplitude is generated on a string. The kinetic energy of any small section of string will be same as its potential energy.
Statement-2 : A standing wave can be written as superposition of two travelling waes. For a wave of small amplitude travelling on string, kinetic energy of any string element is equal to its potential energy at any instant.View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png) View Solution
View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png) View Solution
View SolutionThe equation of a transverse wave propagating in a string is given by
y=0.02sin(x+30t)
where, xandy are in second.
If linear density of the string is 1.3×10−4kg/m, then the tension in the string isView Solution
