A travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidal. The amplitude of vibration is 1.0cm and the displacement becomes zero 200 times per second. The linear mass density of the string is 0.10kgm−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0 the end x= 0 is at its positive extreme position. Write the wave equation. (c ) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10ms.
The correct Answer is:A, B, C, D
Amplitude, A = 1 cm
Tension, T = 90 N
Frequency, f=2002=100Hz
Mass per unit length
m = 0.1 kg//m
(a) V=(Tm)
=√900.1=30m/s
λ=Vf=30100
=0.3=30cm<br>(b)Thewaveequation,<br>y = (1cm) cos 2pi {((t)/(0.01s)) - ((x)/(30)cm)}<br>[because at x = 0 displacement is maximum]
(c ) y=1cos2π(x30−t0.01)
⇒υ=dydt
=(10.01)2πcos2π{(x30)−(t0.01)}
a=dυdt
={4π2(0.01)2}sin2π{(x30)−(t0.01)}
When, x = 50 cm, t = 10 ms = 10 xx10xx10^(-3)s<br>x = ((2pi)/(0.01))sin 2pi{((5)/(3)) - ((0.01)/(0.01))}<br>= - ((pi)/(0.01))sin ((2pixx (2)/(3))<br>=-((1)/(0.01))sin ((4pi)/(3))<br>=200 pi sin ((pi)/(3))<br>200 pi xx (sqrt3)/(2)<br>=544 cm//s = 5.4 m//s<br>Similarly,<br>a = {(4pi^2)/((0.01^2)} cos 2pi {((5)/(3)) - 1}<br>=4pi^2 xx 10^4 xx (1)/(2)<br>=2xx 10^5 cm//s^2 = 2km//s^2
Topper's Solved these Questions
Similar Questions
Knowledge Check
A transverse sinusoidal wave is generted at one end of long, horizontal string by a bar that moves up and down through a distance of 1.00cm. The motion is continuous and is repreated regularly 120 times per second. The string has linear density 90gm/m and is kept under a tension of 900N. Find :
The maximum value of the transverse component of the tension (in newton)A1.8πB10.8πC9D18πA transverse sinusoidal wave is generted at one end of long, horizontal string by a bar that moves up and down through a distance of 1.00cm. The motion is continuous and is repreated regularly 120 times per second. The string has linear density 90gm/m and is kept under a tension of 900N. Find :
What is the maximum power (in watt) transferred along the string.A3.24π2B6.48π2C12.96π2D25.92π2A transverse sinusoidal wave is generted at one end of long, horizontal string by a bar that moves up and down through a distance of 1.00cm. The motion is continuous and is repreated regularly 120 times per second. The string has linear density 90gm/m and is kept under a tension of 900N. Find :
What is the transverse displacement y(in cm) when the minimum power transfer occurs
[Leave the answer in terms of π wherever it occurs]A0B12C14D1
A 200Hz wave with amplitude 1mm travels on a long string of linear mass density 6g/m keep under a tension of 60N.
(a) Find the average power transmitted across a given point on the string.
(b) Find the total energy associated with the wave in a 2.0m long portion of the string.
View SolutionA transverse sinusoidal wave is generated at one end of a long horizontal string by a bar that moves the end up and down through a distance by 2.0cm. the motion of bar is continuous and is repeated regularly 125 times per second. If klthe distance between adjacent wave crests is observed to be 15.6cm and the wave is moving along positive x−direction, and at t=0 the element of the string at x=0 is at mean position y=0 and is moving downward, the equation of the wave is best described by
View SolutionThe displacement of a vibrating string versus position along the string is shown in the figure. The periodic wave have a speed of 10.0cm/s. A and B are two points on the string.
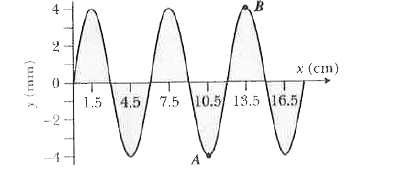
What is the wavelength of the wave?
View SolutionStationary waves are produced in 10 m long stretched string. If the string vibrates in 5 segments and wave velocity 20 m/s then the frequency is :-
View SolutionA string is producing transverse vibration whose equation is y = 0.021 sin ( x + 30 t ) , where x and y are in metre and t is in second . If the linear density of the string is 1.3×10−4kg/m , then tension in string in newton will be
View Solution
