A tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity . Determine the force exerted by the liquid at the other end.
The correct Answer is:a
To solve the problem, we need to determine the force exerted by the liquid at the other end of a tube that is being rotated with a uniform angular velocity. Here's a step-by-step solution:
Step 1: Understand the Setup
We have a tube of length L filled with an incompressible liquid of mass M. The tube is rotated about one of its ends with an angular velocity ω.
Step 2: Consider a Small Element of the Liquid
Let's consider a small element of the liquid at a distance x from the axis of rotation (the end of the tube). The thickness of this element is dx.
Step 3: Determine the Mass of the Small Element
Since the liquid is incompressible, the mass dm of the small element can be expressed as:
dm=MLdx
where ML is the mass per unit length of the liquid.
Step 4: Calculate the Centripetal Force on the Small Element
The centripetal force dF acting on this small element is given by:
dF=dm⋅ω2⋅x
Substituting dm from the previous step:
dF=(MLdx)⋅ω2⋅x
This simplifies to:
dF=Mω2L⋅xdx
Step 5: Integrate to Find the Total Force
To find the total force F exerted by the liquid at the other end of the tube, we need to integrate dF from x=0 to x=L:
F=∫L0dF=∫L0Mω2L⋅xdx
This can be factored as:
F=Mω2L∫L0xdx
Step 6: Evaluate the Integral
The integral ∫L0xdx is calculated as:
∫L0xdx=(x22)L0=L22
Substituting this back into the equation for F:
F=Mω2L⋅L22=MLω22
Final Result
Thus, the force exerted by the liquid at the other end of the tube is:
F=MLω22
We have a tube of length L filled with an incompressible liquid of mass M. The tube is rotated about one of its ends with an angular velocity ω.
Let's consider a small element of the liquid at a distance x from the axis of rotation (the end of the tube). The thickness of this element is dx.
Since the liquid is incompressible, the mass dm of the small element can be expressed as:
dm=MLdx
where ML is the mass per unit length of the liquid.
The centripetal force dF acting on this small element is given by:
dF=dm⋅ω2⋅x
Substituting dm from the previous step:
dF=(MLdx)⋅ω2⋅x
This simplifies to:
dF=Mω2L⋅xdx
To find the total force F exerted by the liquid at the other end of the tube, we need to integrate dF from x=0 to x=L:
F=∫L0dF=∫L0Mω2L⋅xdx
This can be factored as:
F=Mω2L∫L0xdx
The integral ∫L0xdx is calculated as:
∫L0xdx=(x22)L0=L22
Substituting this back into the equation for F:
F=Mω2L⋅L22=MLω22
Thus, the force exerted by the liquid at the other end of the tube is:
F=MLω22
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - NCER EXAMPLAR PROBLEMS
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ASSERTION AND REASON
15 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ROLLING MOTION
16 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions
150 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
Similar Questions
A tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. The force exerted by the liquid at the other end is
View SolutionA plane mirror of length L moves about one of its ends
View SolutionOne end of a uniform rod of mas m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity ω. The force exerted by the clamp on the rod has a horizontal component
View SolutionA uniform of mass m and length L is tied to a vertical shaft. It rotates in horizontal plane about the vertical axis at angular velocity ω. How much horizontal force does the shaft exert on the rod?

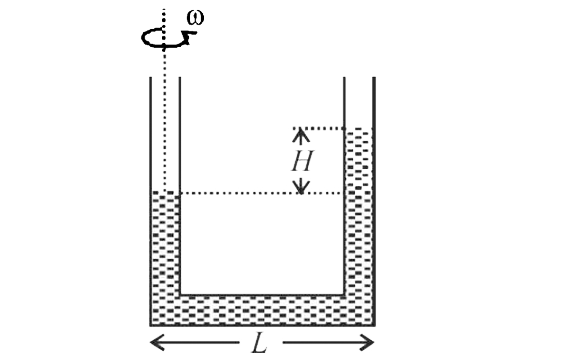
View SolutionA U tube is rotated about one of it's limbs with an angular velocity ω. Find the difference in height H of the liquid (density ρ) level, where diameter of the tube d<<L.
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The graph of the pressure gradient (dPdx) with the distance x meaured from the axis of rotation is :
View SolutionA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
View Solution
