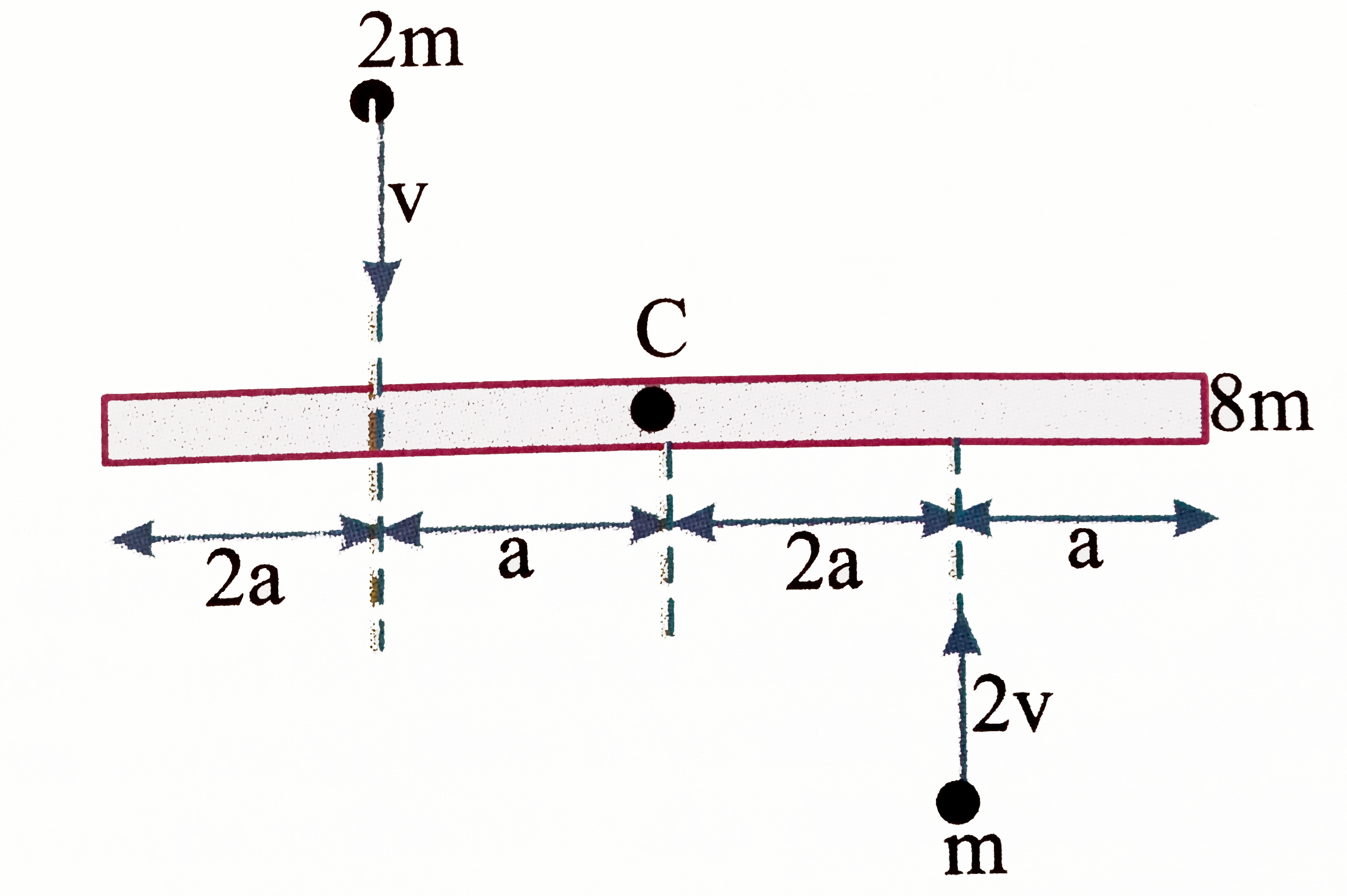
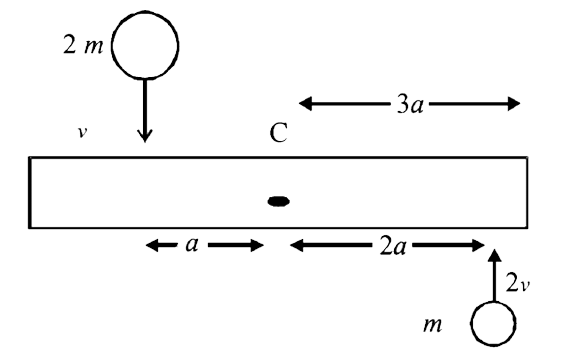
A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively, strike the bar (as shown in figure) and stick to the bar after collision. Calculate (a) velocity of the centre of mass (b) angular velocity about centre of mass and (c) total kinetic energy, just after collision.
E=3mv25
E=(3mv2)
E=3mv5
None
The correct Answer is:A
a. In the process of collision the linear momentum remains constant
2mv−m2(2v)+0=(2m+m=8m)vCM
or vCM=0
b. Angular momentum of the system also remains constant Therefore,
2mva+m(2v)(2a)+0=Iω ..i
Where I is the moment of inertia of the system after collision.
I=M.I. of the rod +M.I.of mass 2m+M.I. of the m
or I=(8m)(6a2)12+2ma2+m(2a)2
substituting this value in eqn i we get ω=v5a
E=12Iω2=1230ma2×(vl5a)2
or E=3mv25
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.3
21 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
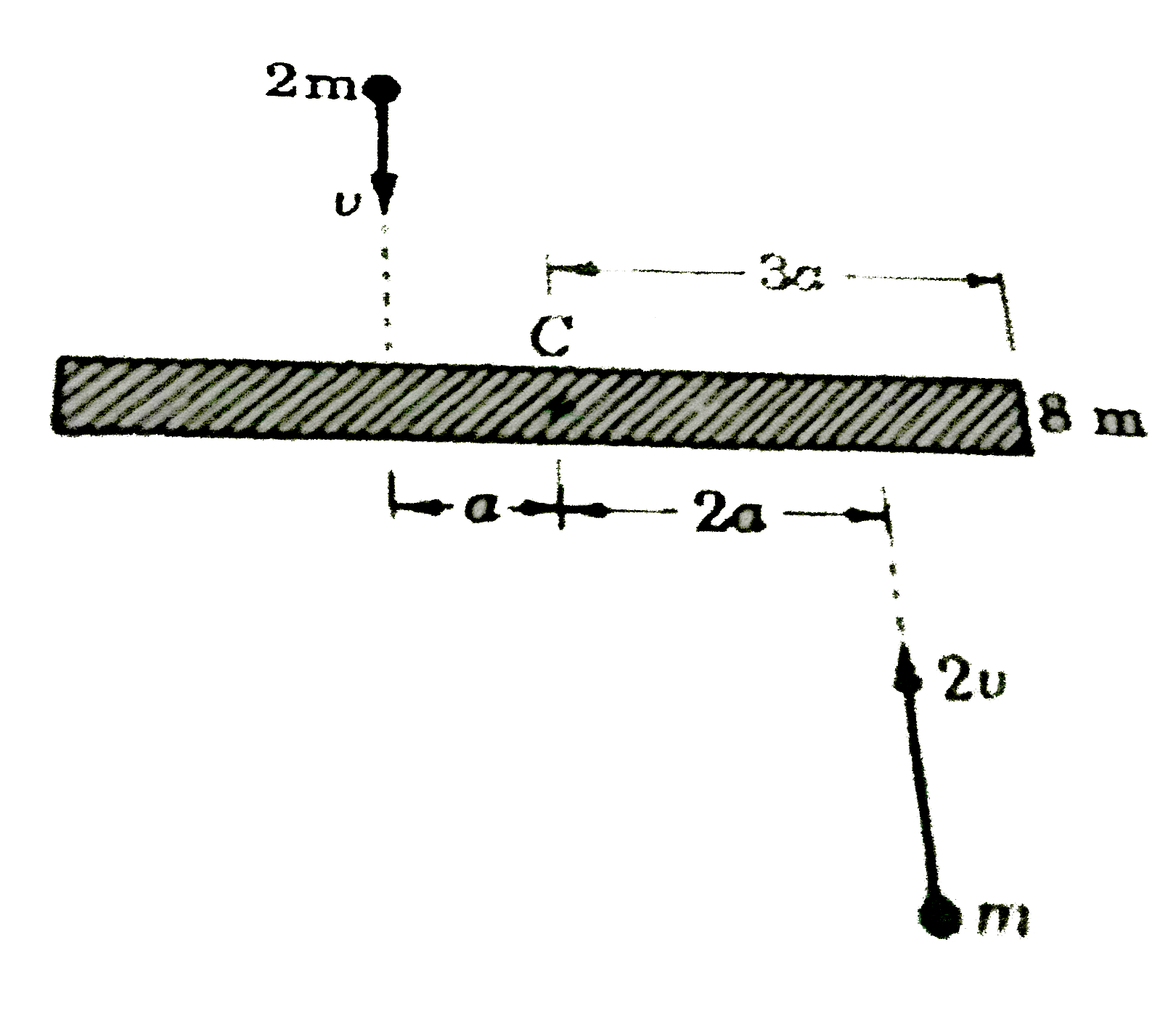
A uniform bar of length 6a and mass 8 m lies on a smooth horizontal table. Two point-masses m and 2m moving in the same horizontal plane with speeds 2v and v respectively strike the bar as shown in Fig, and stick to the bar after collision.
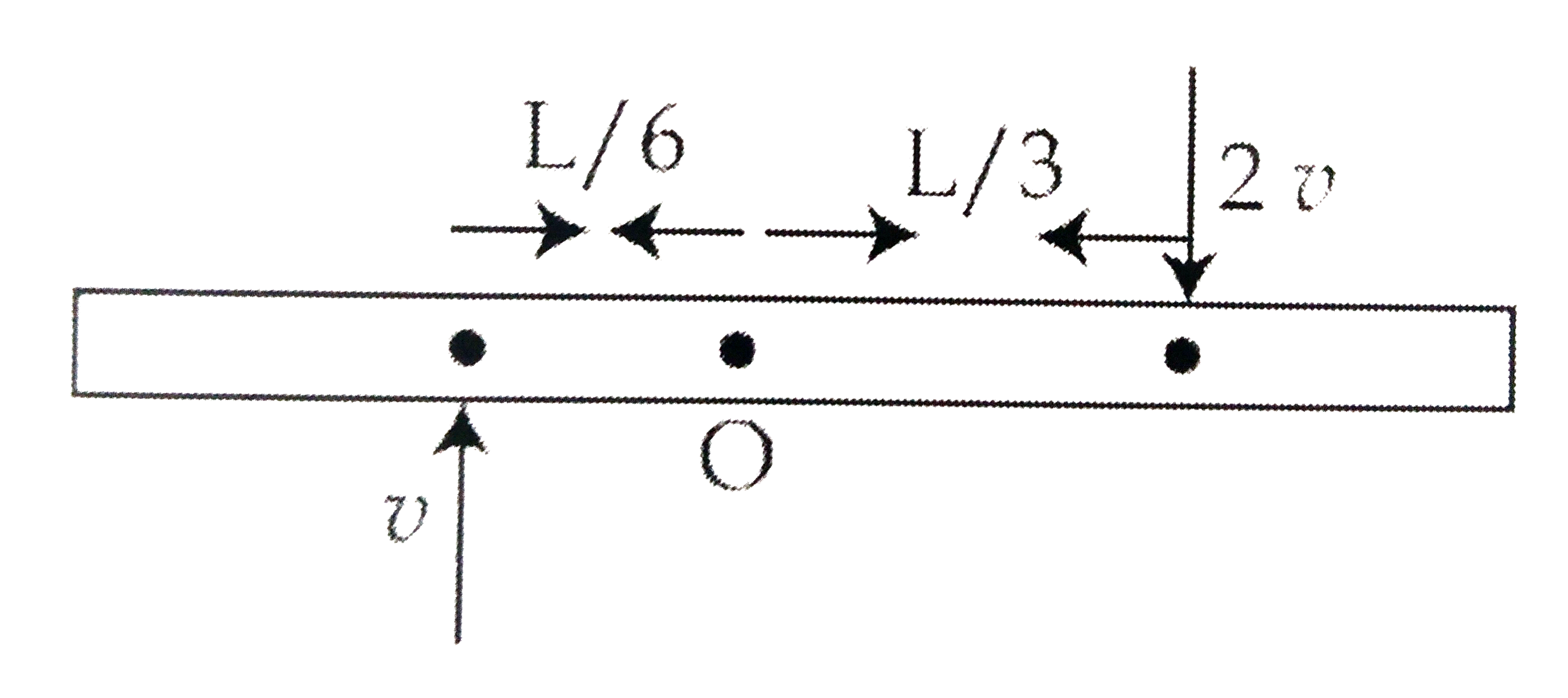
View SolutionA thin uniform bar of length L and mass 8m lies on a smooth horizontal table .Two point masses m and 2 m are moving in the same horizontal plane from opposite sides of the bar with speeds 2v and v respectively .The masses stick to the bar after collision at a distances L3andL6 respectively from the center of the bar if the bar starts rotating about its center of mass as result of collision the angular speed of the bar will be
View Solution
Knowledge Check
A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v, respectively, strike the bar (as shown in the figure) and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by ω, E and VC, respectively, we have after collision
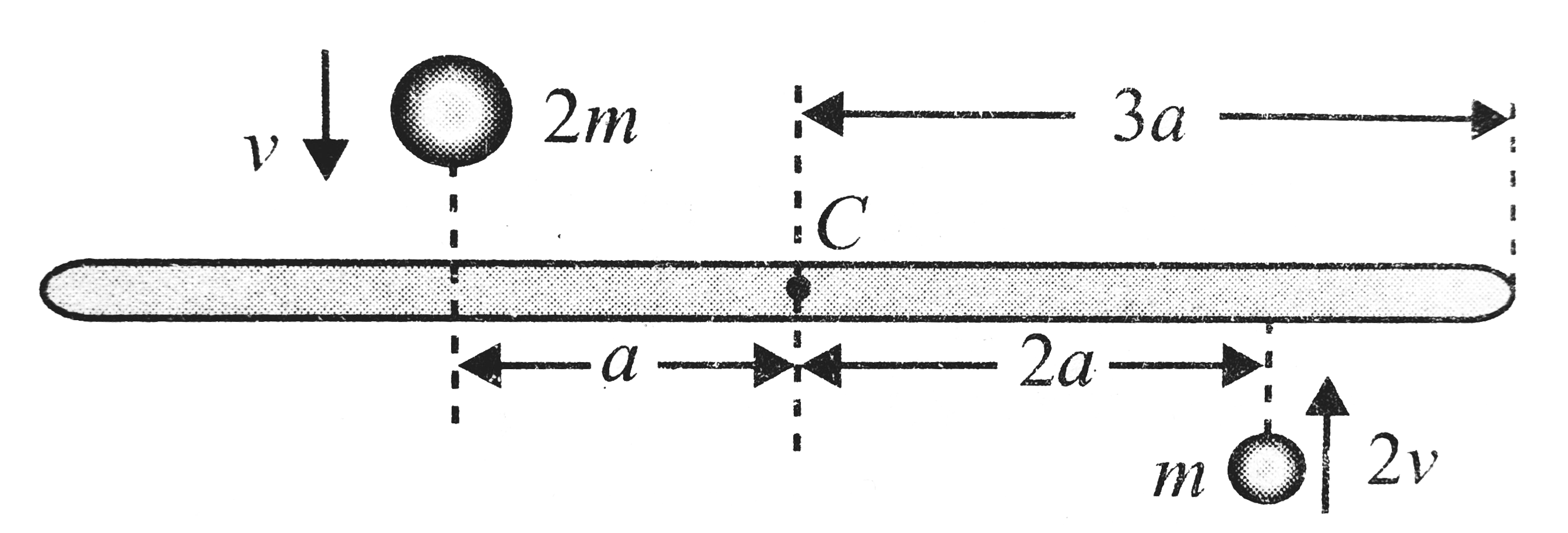 AVc=0Bω=3v5aCω=v5aDE=3mv25
AVc=0Bω=3v5aCω=v5aDE=3mv25A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar [as shown in the fig.] and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by ω, E and vc respecitvely, we have after collison
 Avc=0Bω=3v5aComeag=v5aDE=3mv25
Avc=0Bω=3v5aComeag=v5aDE=3mv25A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving with the same horizontal speed 2v and v respectively, strike the bar as shown in the figure and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy, and centre of mass velocity after collision by ω, E and vC respectively, we have after collision
 AvC=0Bω=3v5aCω=v5aDE=3mv25
AvC=0Bω=3v5aCω=v5aDE=3mv25
A.uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar and stick to the bar. The bar is set in rotation. The rotational energy E=pmv2q then find (p+q).
'(##CEN_KSR_PHY_JEE_C09_E01_038_Q20##)'
View SolutionA uniform rod of length λ lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out.
The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point of mass m moving horizontally at right angle to the rod with velocity v collides with one end of the rod and sticks to it, then:
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View Solution
