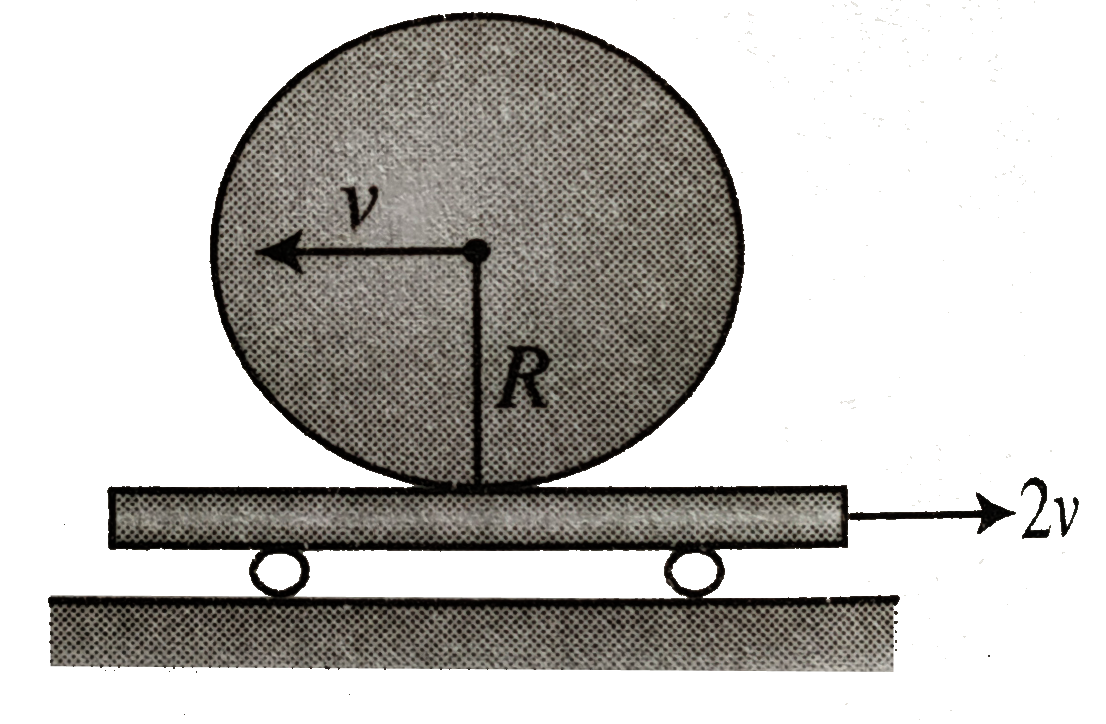
A uniform disc is spun with an angular velocity ω and simultaneously projected with a linear velocity v towards left on a plank, while the plank moves towards right with a constant velocity 2v. If the disc rolls without sliding on the plank just after its spinning, find the magnitude of →ω. (Take v=3ms−1,R=1m)
The correct Answer is:9rad/s
For pure rolling of the disc on the plank
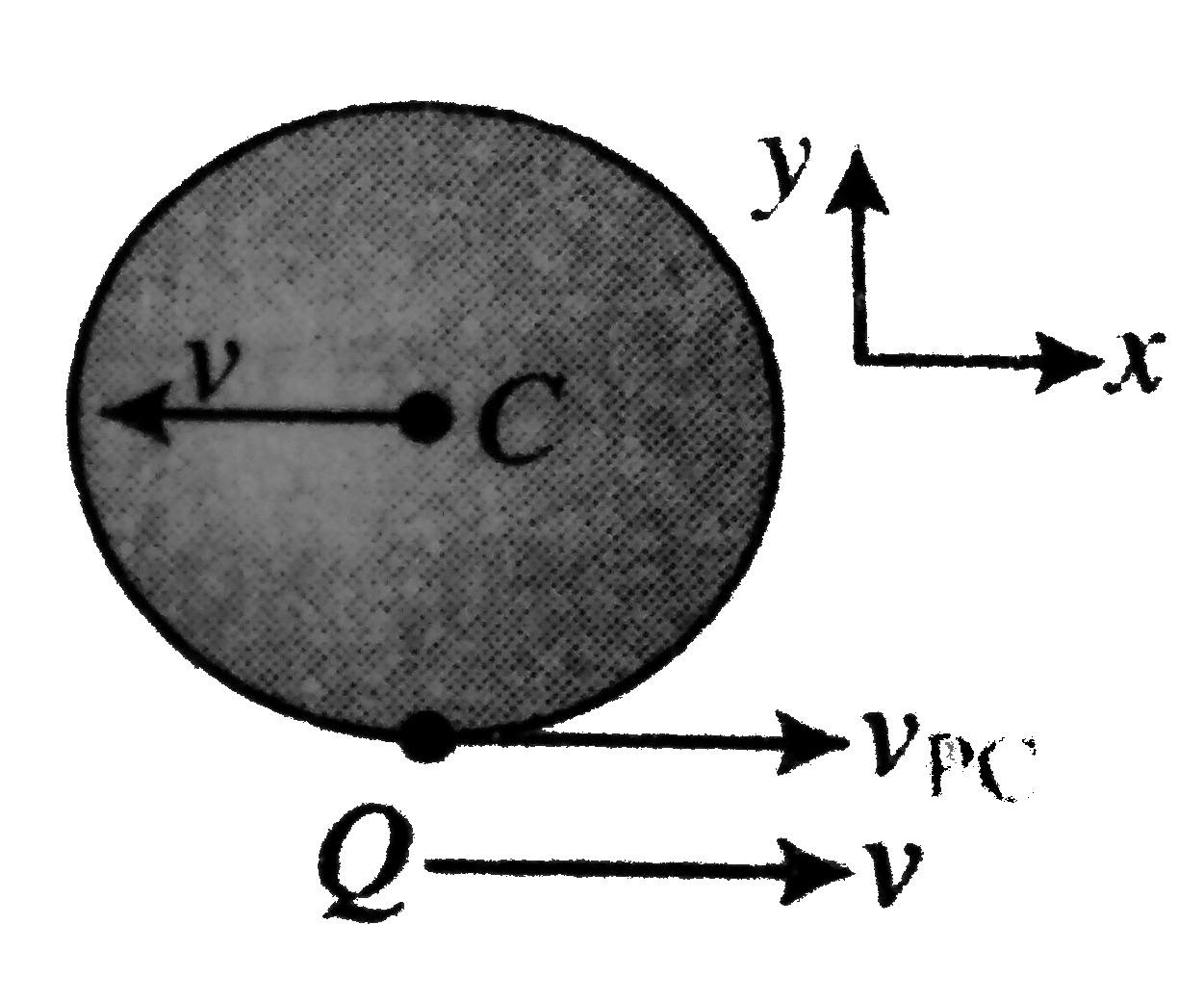
→vP=→vQ, where →vQ=2vˆi
This gives →vP=2→v
Since →vp=→vPC=→vC
Substituting →vP=2vˆi and →vC=−→vˆi
we have→vPC=3vˆi
Then using the formula →vPC=→ωPC×→rPC
Where →rPC=−Rˆj
we can find →ωPC(=→ω)=3vrˆk
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.

View SolutionA uniiform disc of radius r spins with angular velocity ω and angular acceleration α. If the centre of mass of the disc has linear acceleration a, find the magnitude and direction of aceeleration of the point 1,2, and 3.

View Solution
Knowledge Check
A uniform rod AB of length l rotating with an angular velocity ω while its centre moves with a linear velocity v=ωl6 If the end A of the rod is suddenly fixed, the angular velocity of
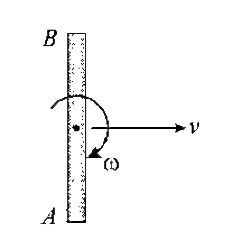 A34ωBω3Cω2D23ω
A34ωBω3Cω2D23ωA uniform disc of mass m is fitted (pivoted smoothly) with a rod of mass m/2. If the bottom of the rod os pulled with a velocity v, it moves without changing its and of orientation and the disc rolls without sliding. Take kinetic energy of the system (rod + disc) is.
 .Amv24Bmv22C5mv216Dmv2
.Amv24Bmv22C5mv216Dmv2A disc is given an angular velocity ω0 and a linear velocity v0 as shown in the figure. It is released on a rough horizontal surface of friction coefficient μ. Mark the correct statement (ω0=3v0/R)
 AThe frictional force will be μmg during the entire motion.BAfter some time the disc will start rolling without sliding along positive x-axis.CAfter some time the disc will start rolling without sliding along negative x-axis.DThe mechnical energy of the disc will remain conserved.
AThe frictional force will be μmg during the entire motion.BAfter some time the disc will start rolling without sliding along positive x-axis.CAfter some time the disc will start rolling without sliding along negative x-axis.DThe mechnical energy of the disc will remain conserved.
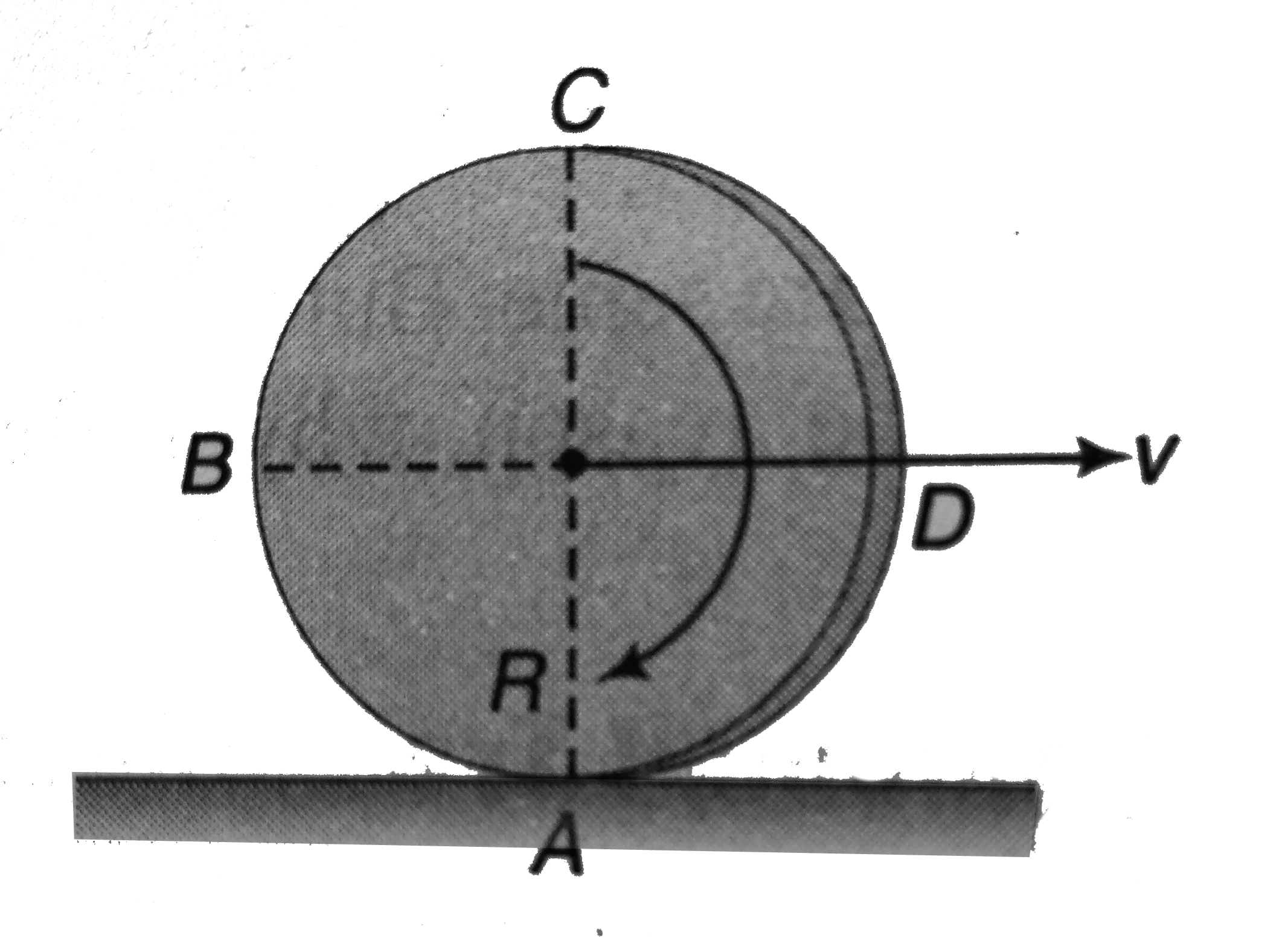
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
View SolutionThe rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.

View SolutionA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that

View Solution
