A uniform electric field E is established between two parallel charged plates as shown in figure. An electron enter the field symmetrically between the plates with a speed u. The length of each plate is l. if the electron does not stricke any of the plates, find the angle of deviation of the electron as it comes out of the field at the outer end of plates. [tan−1(eElμ2)]
![A uniform electric field E is established between two parallel charged plates as shown in figure. An electron enter the field symmetrically between the plates with a speed u. The length of each plate is l. if the electron does not stricke any of the plates, find the angle of deviation of the electron as it comes out of the field at the outer end of plates. [tan^(-1) ((eEl)/(mu^(2)))]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/GAL_PHY_V03A_ECA_C01_E01_116_Q01.png)
E
s
l2
u−2
The correct Answer is:A, B, C, D
Step by step video, text & image solution for A uniform electric field E is established between two parallel charged plates as shown in figure. An electron enter the field symmetrically between the plates with a speed u. The length of each plate is l. if the electron does not stricke any of the plates, find the angle of deviation of the electron as it comes out of the field at the outer end of plates. [tan^(-1) ((eEl)/(mu^(2)))] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A uniform electric field E=91×10−6V/m is created between two parallel, charged plates as shown in figure. An electron enters the field symmetrically between the plates with a speed v0=4×103m/s. The length of each plates is l=1m. Find the angle of deviation of the path of the electron as it comes out of the field. (Mass of the electron is m=9.1×10−31kg and its charge is e=−1.6×10−19C).

View SolutionA stream of electrons moving with a velocity of 3×107ms−1 is deflected by 2 mm in traversing a distance of 0.1 m in a uniform electric field of strength 18Vm−1 in Fig. 1.42. An electron enters the field symmetrically between the plates with a speed υ0. The length of each plate is l. Find the angle of deviation of the bath of the electron as it comes out of the field.
View Solution
Knowledge Check
A uniform electric field E is created between two parallel charged plates as shown in figure . An electron enters the field symmetrically between the plates with a speed v0. The length of each plate is l. Find the angle of deviation of the path of the electron as it comes out of the field.
 Aθ=tan−1(el)mv20Bθ=tan−1(eEl)v20Cθ=tan−1(eEl)mv20Dθ=tan−1(eEl)v20
Aθ=tan−1(el)mv20Bθ=tan−1(eEl)v20Cθ=tan−1(eEl)mv20Dθ=tan−1(eEl)v20A uniform electric field →E exists between the plates of a charged condenser. A charged particle enters the space between the plates and perpendiculars to →E. The path of the particle between the plates is a
AStraight lineBhyperbolaCparabolaDcircleThe electric field (→E) between two parallel plates of a capacitor will be uniform if.
Athe plate separation (d) is equal to area of the plate (A)Bthe plate separation (d) greater when compared to area of the plate (A)Cthe plate separation (d) is less when compared to area of the plate (A)D2 (or) 3
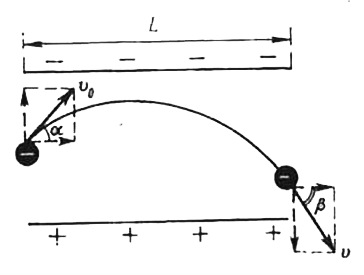
An electric field of intensity E is set up between two parallel plates of length L. An electron beam enters the field at an angle α>0 to the plates and leaves it at an angle β<0 (Fig.). Find the initial velocity of the electrons. The force of gravity is to be neglected.
View SolutionA uniform electric field 'E' exists between two parallel plates having opposite having opposite charge on each plates. An electron enters the field between the plates with speed v0 as shown in the figure. If length of each plate is l then angle with which electron deviates from its initial path is (m is mass of electron ) (##AAK_TST_05_NEET_YEAR(19)_PHY_E05_133_Q01##)
View SolutionAn electron (e,m) is projected into a uniform electric field E vertically downward between parallel plates at separation d, with velocity v0. The electron enters the electric field at a point midway between the plates. Find
(a) the magnitude of electric field if electron emerges from the electric field just at the edge of upper plate.
(b) the direction of the velocity of electron as it emerges from the electric field.
(c ) the equation of trajectory followed by electron.
The length of plates is L and consider only electric force.
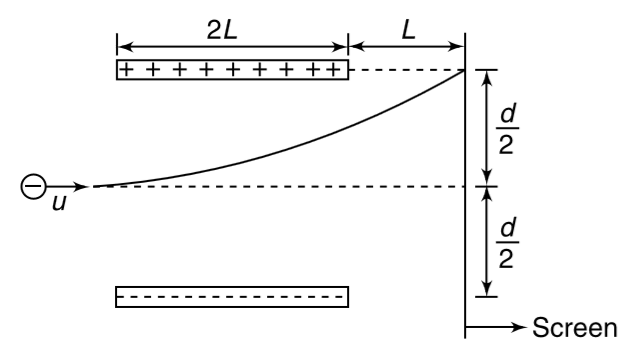
View SolutionAn electron (charge = e, mass = m) is projected horizontally into a uniform electric field produced between two oppositely charged parallel plates, as shown in figure. The charge density on both plates is ± σC/m2 and separation between them is d. You have to assume that only electric force acts on the electron and there is no field outside the plates. Initial velocity of the electron is u, parallel to the plates along the line bisecting the gap between the plates. Length of plates is 2L and there is a screen perpendicular to them at a distance L. (i) Find s if the electron hits the screen at a point that is at same height as the upper plate.
(ii) Final the angle q that the velocity of the electron makes with the screen while it strikes it.
View Solutionv33.2
View Solution
