A uniform electric field 'E' exists between two parallel plates having opposite having opposite charge on each plates. An electron enters the field between the plates with speed v0 as shown in the figure. If length of each plate is l then angle with which electron deviates from its initial path is (m is mass of electron ) (##AAK_TST_05_NEET_YEAR(19)_PHY_E05_133_Q01##)
tan−1(eEl2mv20)
tan−1(eElmv20)
sin−1(eElmv20)
sin−1(eEl2mv20)
To solve the problem of an electron entering a uniform electric field between two parallel plates, we will follow these steps:
Step 1: Understand the motion of the electron
The electron enters the electric field with an initial horizontal velocity v0. The electric field E will exert a force on the electron, causing it to accelerate vertically. The force on the electron due to the electric field is given by:
F=qE
where q is the charge of the electron. The acceleration ay of the electron in the vertical direction can be expressed as:
ay=Fm=qEm
where m is the mass of the electron.
Step 2: Determine the time of flight
The length of the plates is L. The time T taken by the electron to travel the length of the plates can be calculated using its horizontal velocity v0:
T=Lv0
Step 3: Calculate the vertical displacement
The vertical displacement y of the electron while it is between the plates can be calculated using the kinematic equation:
y=vy0T+12ayT2
Since the initial vertical velocity vy0 is 0 (the electron enters horizontally), this simplifies to:
y=12ayT2
Substituting ay and T:
y=12(qEm)(Lv0)2
Step 4: Relate vertical and horizontal components
The angle θ with which the electron deviates from its initial path can be found using the tangent function:
tanθ=yL
Substituting for y:
tanθ=12(qEm)(Lv0)2L
This simplifies to:
tanθ=qEL2mv20
Step 5: Find the angle θ
Finally, we can express the angle θ as:
θ=tan−1(qEL2mv20)
Final Result
Thus, the angle with which the electron deviates from its initial path is:
θ=tan−1(qEL2mv20)
The electron enters the electric field with an initial horizontal velocity v0. The electric field E will exert a force on the electron, causing it to accelerate vertically. The force on the electron due to the electric field is given by:
F=qE
where q is the charge of the electron. The acceleration ay of the electron in the vertical direction can be expressed as:
ay=Fm=qEm
where m is the mass of the electron.
The length of the plates is L. The time T taken by the electron to travel the length of the plates can be calculated using its horizontal velocity v0:
T=Lv0
The vertical displacement y of the electron while it is between the plates can be calculated using the kinematic equation:
y=vy0T+12ayT2
Since the initial vertical velocity vy0 is 0 (the electron enters horizontally), this simplifies to:
y=12ayT2
Substituting ay and T:
y=12(qEm)(Lv0)2
The angle θ with which the electron deviates from its initial path can be found using the tangent function:
tanθ=yL
Substituting for y:
tanθ=12(qEm)(Lv0)2L
This simplifies to:
tanθ=qEL2mv20
Finally, we can express the angle θ as:
θ=tan−1(qEL2mv20)
Thus, the angle with which the electron deviates from its initial path is:
θ=tan−1(qEL2mv20)
Topper's Solved these Questions
Similar Questions
A uniform electric field E=91×10−6V/m is created between two parallel, charged plates as shown in figure. An electron enters the field symmetrically between the plates with a speed v0=4×103m/s. The length of each plates is l=1m. Find the angle of deviation of the path of the electron as it comes out of the field. (Mass of the electron is m=9.1×10−31kg and its charge is e=−1.6×10−19C).

View SolutionA uniform electric field E is established between two parallel charged plates as shown in figure. An electron enter the field symmetrically between the plates with a speed u. The length of each plate is l. if the electron does not stricke any of the plates, find the angle of deviation of the electron as it comes out of the field at the outer end of plates. [tan−1(eElμ2)]

View Solution
Knowledge Check
A uniform electric field E is created between two parallel charged plates as shown in figure . An electron enters the field symmetrically between the plates with a speed v0. The length of each plate is l. Find the angle of deviation of the path of the electron as it comes out of the field.
 Aθ=tan−1(el)mv20Bθ=tan−1(eEl)v20Cθ=tan−1(eEl)mv20Dθ=tan−1(eEl)v20
Aθ=tan−1(el)mv20Bθ=tan−1(eEl)v20Cθ=tan−1(eEl)mv20Dθ=tan−1(eEl)v20v33.2
A0.34 mmnB0.57 mmC7.5 mmD0.75 mmTwo parallel plates carry opposite charges such that the electric field at the space between them is in upward direction ,.An electron is shot in the space and parallel to the plates.its deflection from the original directions will be
AupwardsBDownwardsCCircularDDoes not deflect
A uniform electric field E exists between two oppositely charged plates (Fig. 3.38). What will be the work done in moving a charge q along a closed rectangular path ?
 .
.
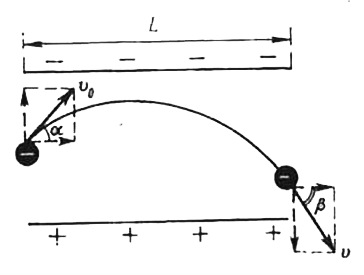
View SolutionAn electric field of intensity E is set up between two parallel plates of length L. An electron beam enters the field at an angle α>0 to the plates and leaves it at an angle β<0 (Fig.). Find the initial velocity of the electrons. The force of gravity is to be neglected.
View SolutionTwo large conducting plates of a parallel plate capacitor are given charges Q and 3Q respectively. If the electric field in the region between the plates is E0 , then the force of interaction between the plates is

View SolutionA parallel plate capacitor has a uniform electric field →E in the space between the plates. If the distance between the plates is 'd' and the area of each plate is 'A' the energy stored in the capacitor is
View SolutionTwo parallel plates carry opposites charges such that the electric field in the space between them is in upward direction. An electron is shot in the space and parallel to the plates . Its deflection from the original direction will be
View Solution
