A cylinder is released from rest from the top of an incline of inclination θ and length. If the cylinder rolls without slipping. What will be its speed whenit reaches the bottom?
Let the mass of the cylinder be m and its radilus r. Suippose the linear spee of the cylinder when it reaches the bottom is v. As the cylinder rolls without slilpping, its angular speed about its axis is ω=vr. The kinetic energy at the bottom will be
K=12Iω2+12mv2
=12(12mr2)ω2+12mv2=14+12mv2=34mv2
This should be equal to the loss of potential energy mgl sintheta.Thus,3/4mv^2=mglsintheta<br>or v=sqrt(4/3gl sin theta)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Short Answer
22 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
A hollow sphere is released from the top of an inclined plane of inclination θ and length L. If a hollow sphere rolls without slipping, what will be its speed when it reaches the bottom?
View SolutionA hollow sphere is released from top of an inclined plane of inclination 30° and length of inclined plane is I. If sphere rolls without slipping then its speed at bottom is
View Solution
Knowledge Check
A cylinder is released from rest from the top of an incline of inclination θ and length l. If the cylinder roles without slipping, its speed at the bottom
A√4glsinθ3B√3glsinθ2C√4gl3sinθD√4gsinθ3lA cylinder of mass 2 kg is released from rest from the top of an inclined plane of inclination 30∘ and length 1m. If the cylinder rolls without slipping, then its speed when it reaches the bottom, is [Take, g = 10 m/s2]
A203 m/sB√203 m/sC103 m/sD√103 m/sA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
AThe friction force is dissipativeBThe friction force is necessarily changingCThe friction force will aid rotation but hinder translationDThe friction force is reduced if θ is reduced
A hollow sphere is released from top of an inclined plane of inclination 30º and length of inclined plane is L. If sphere rolls without slipping then its speed at bottom is
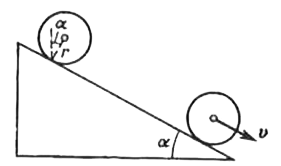
View SolutionA solid cylinder with base radius jis placed on top of an inclined plane of length land slope angle α (Fig). The cylinder rolls down without slipping. Find the speed of the centre of mass of the cylinder at the bottom of the plane, if the coefficient of rolling friction is k. Can rolling friction be neglected? Do the calculation for the following conditions: l=1m,α=30∘,r=10cm,k=5×10−4m . What would be the speed if, in the absence of friction, the cylinder slides down?
View SolutionA hollow cylinder and a solid cylinder having the same mass and diameter are released from rest simultaneously from the top of an inclined plane. They roll without slipping which will reach the bottom firstly
View SolutionTwo spheres of unequal masses but of the same radii are released from the top of a smooth inclined plane. They roll down the plane without slipping. Which one will reach the bottom first?
View SolutionTwo objects, a ring and a spherical shell of same mass and radius are released from the top of two Identical inclined plane. If they are rolling without slipping, then ratio of speed of center of mass of the two objects when they will reach the bottom of the inclined plane is
View Solution