A uniform magnetic field B=B0tˆi in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.
The flux linked with loop is
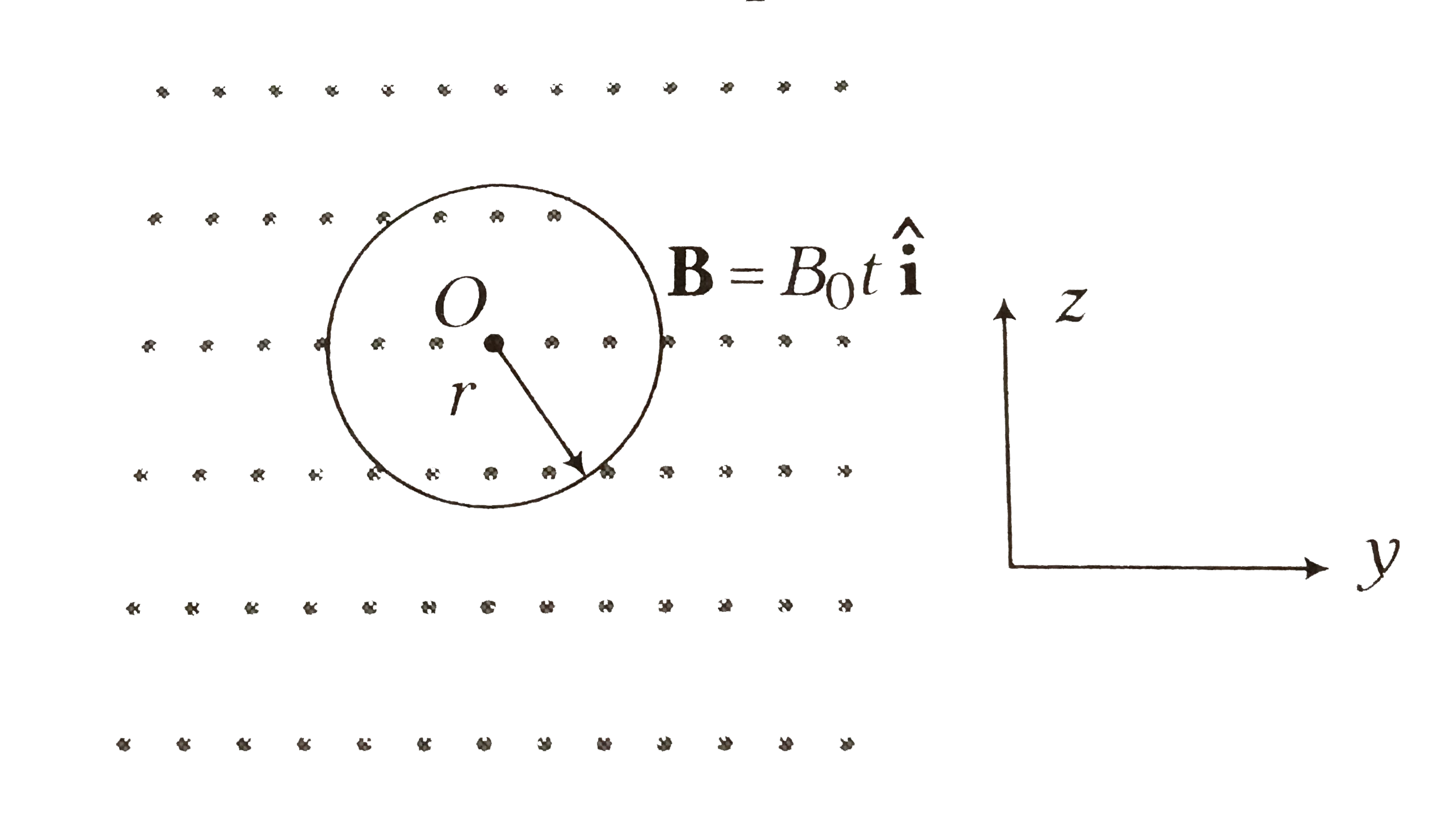
We know that magnetic flux is given as
ϕB=B.S=(B0t)(πr2)cos0∘
⇒ ϕB=B0πr2t and dϕdt=B0πr2
Further, induced emf, ε=−dϕdt=−B0πr2
Therefore, current, i=|ε|R=B0πr2R
By Lenz's law, i should be clockwise, so that it can oppose the increase in magnetic field.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 13videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 22videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
There exists a uniform magnetic field ¯¯¯B=B0t¯k in a region. A circular conducting loop of radius r and resistance R is placed with its plane in x-y plane. Determine the current through the loop and sense of the current.
View SolutionA space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R.
Show the direction of the current when the loop is entering into the region II.View Solution
Knowledge Check
- Question 1 - Select One
A circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
Adirectly proportional to r.BzeroCinversely proportional to r.Ddirectly proportional to I. - Question 2 - Select One or More
An external magnetic field is decreased to zero, due to which a current is induced in a circular wire loop of radius r and resistance R placed in the field. This current will not become zero at the instant when B stops changing
AAt the instant when external magnetic field stops changing (t=0), the current in the loop is i0. The current in the loop as a function of time for t>0 is given by i0e−2Rt/μ0π.BFor the same as in option (a), the current in the loop as a function of time t=0 is given by μ0iR2r.CThe time in which current in loop decreases to 10−3i0 (from t=0) for R=100Ω and r=5cm is given by 3π21n101010s.DFro the same as in option (c), the time in which current in loop decreases to 10−3i0 (from t=0) for R=100Ω and r−5cm is given by 3π2106s. - Question 3 - Select One
What will be magnetic field at centre of current carrying circular loop of radius R?
Aμ0I4πRBμ0I2πRCμ0I2RDzero
A space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R.
Obtain an expression for the magnitude of the induced current in the loop.View SolutionA space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R.
Plot a graph between the induced emf and the time of rotation for two periods of rotation.View SolutionSpace is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.
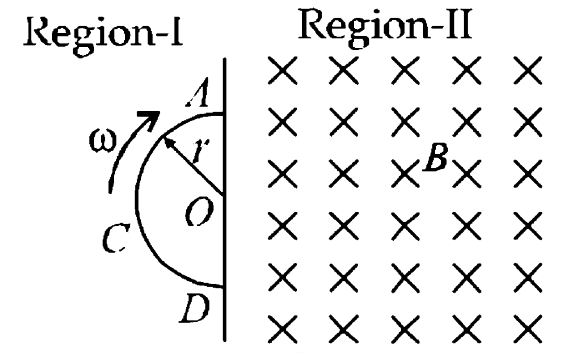
(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.View SolutionThe graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conducting loop, with the direction of the field perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first.
 View Solution
View SolutionThe magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
View Solution

