A uniform rod of length b can be balanced as shown in figure. The lower end of the rod is resting against a vertical wall. The coefficient of friction between the rod and the wall and that between the rod and the support at A is μ. Distance of support from the wall is a.
(a) Find the ratio ab if the maximum value of θ is θ1.
(b) Find the ratio ab if the minimum value of θ is θ2.
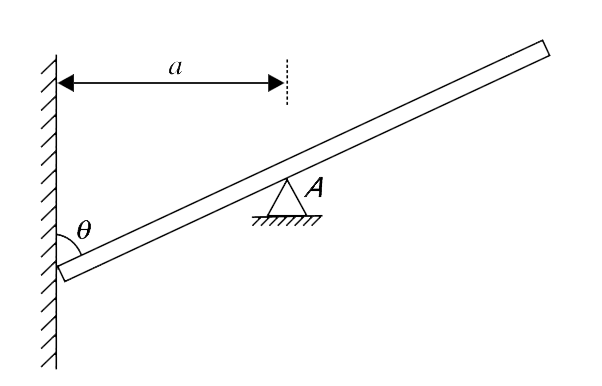
The correct Answer is:(a) ab=12sin2θ1[(1−μ2)sinθ1−2μcosθ1]
(b) ab=12sin2θ2[(1−μ2)sinθ2+2μcosθ2]
Topper's Solved these Questions
Similar Questions
A uniform rod is made to lean between a rough vertical wall and the ground. The coefficient of friction between the rod and the ground is μ1 and between the rod and the wall is μ2. Find the angle at which the rod can he leaned without slipping.
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View Solution
Knowledge Check
A rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is 4m/s along the wall. Find the velocity of end B, when end B makes 30∘ with wall PQ.
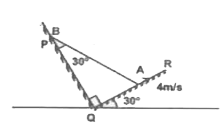 A8m/sB2√3m/sC4√3m/sD4√3m/s
A8m/sB2√3m/sC4√3m/sD4√3m/s
A ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?

View SolutionA rod of mass M and length L lies on an incline having inclination of θ=37∘. The coefficient of friction between the rod and the incline surface is μ=0.90. Find the tension at the mid point of the rod.
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionIn the diagram shown, friction is present only between therod and the wall. The mass of the rod is M and tht of the wedge is 3M. What is the minimum value of the coefficient of friction between the rod and the wall so that rod remains in the state of rest?
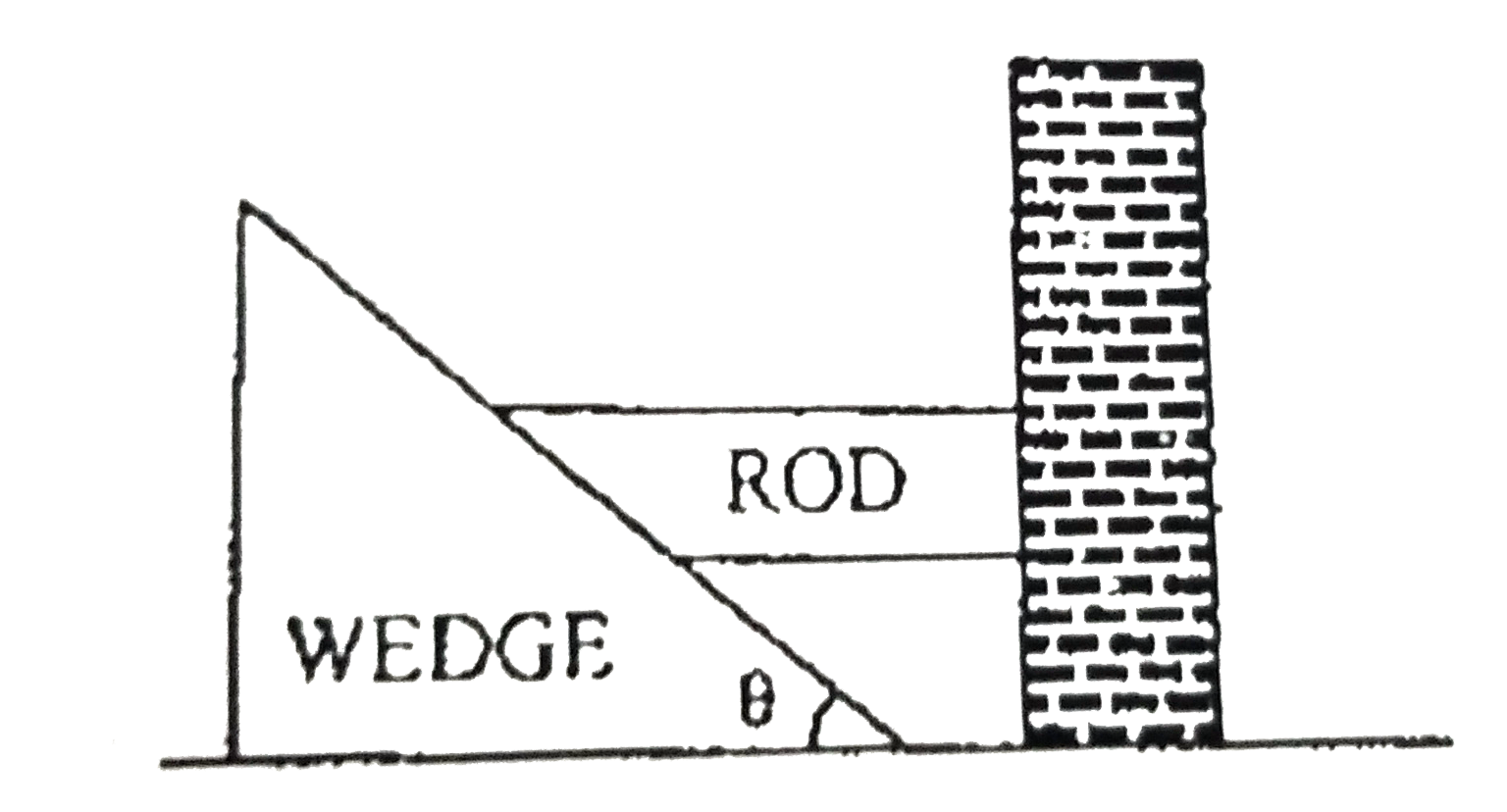
View SolutionA conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View SolutionA rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is 4m/s along the wall. Find the velocity of end B, when end B makes 30∘ with wall PQ.

View SolutionA conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
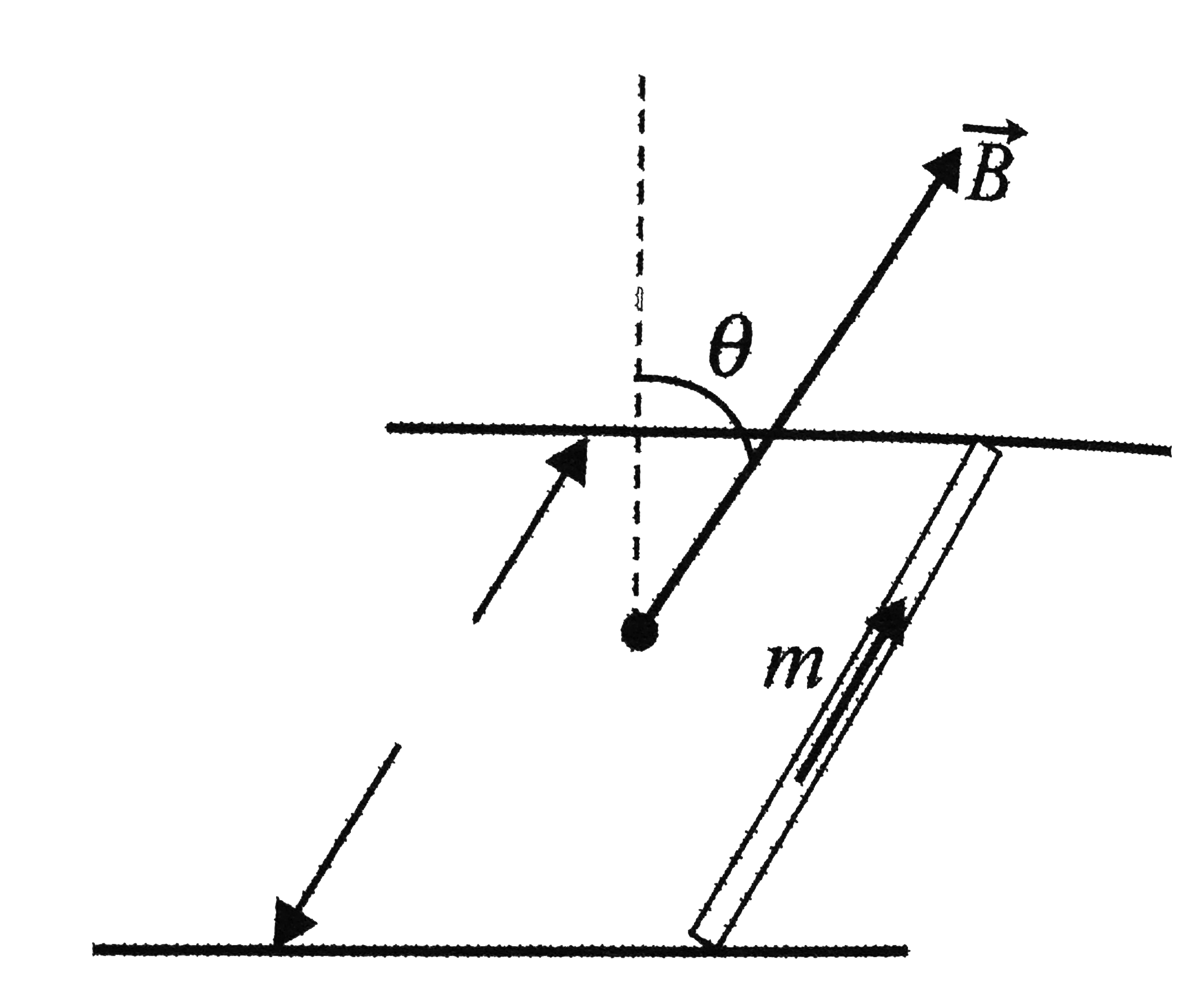
View Solution
