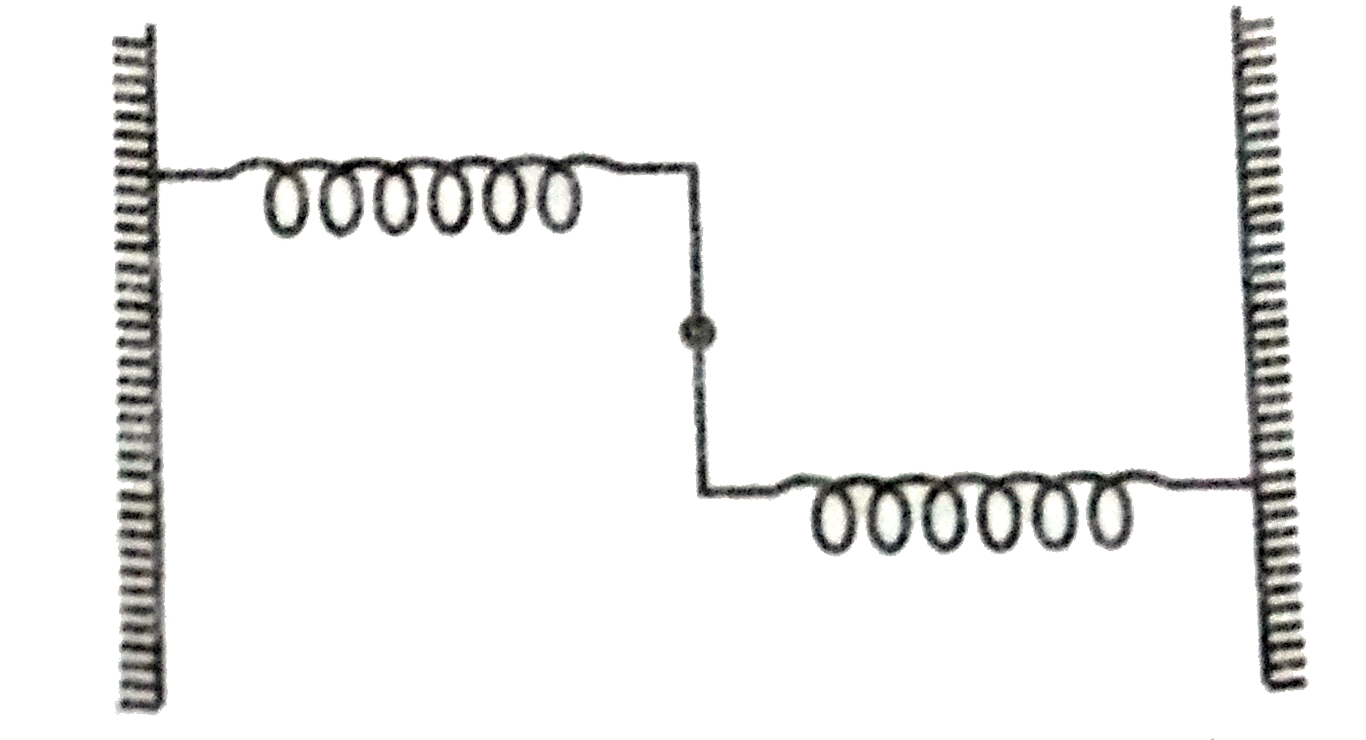
A uniform rod of length l and mass M is pivoted at the centre. Its two ends are attached to two ends are attached to two springs of equal spring constant k. the springs are fixed to rigid support as shown in figure and the rod is free to oscillate in the horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscillation is
12π√2k6M
12π√kM
12π√6kM
12π√24kM
The correct Answer is:C
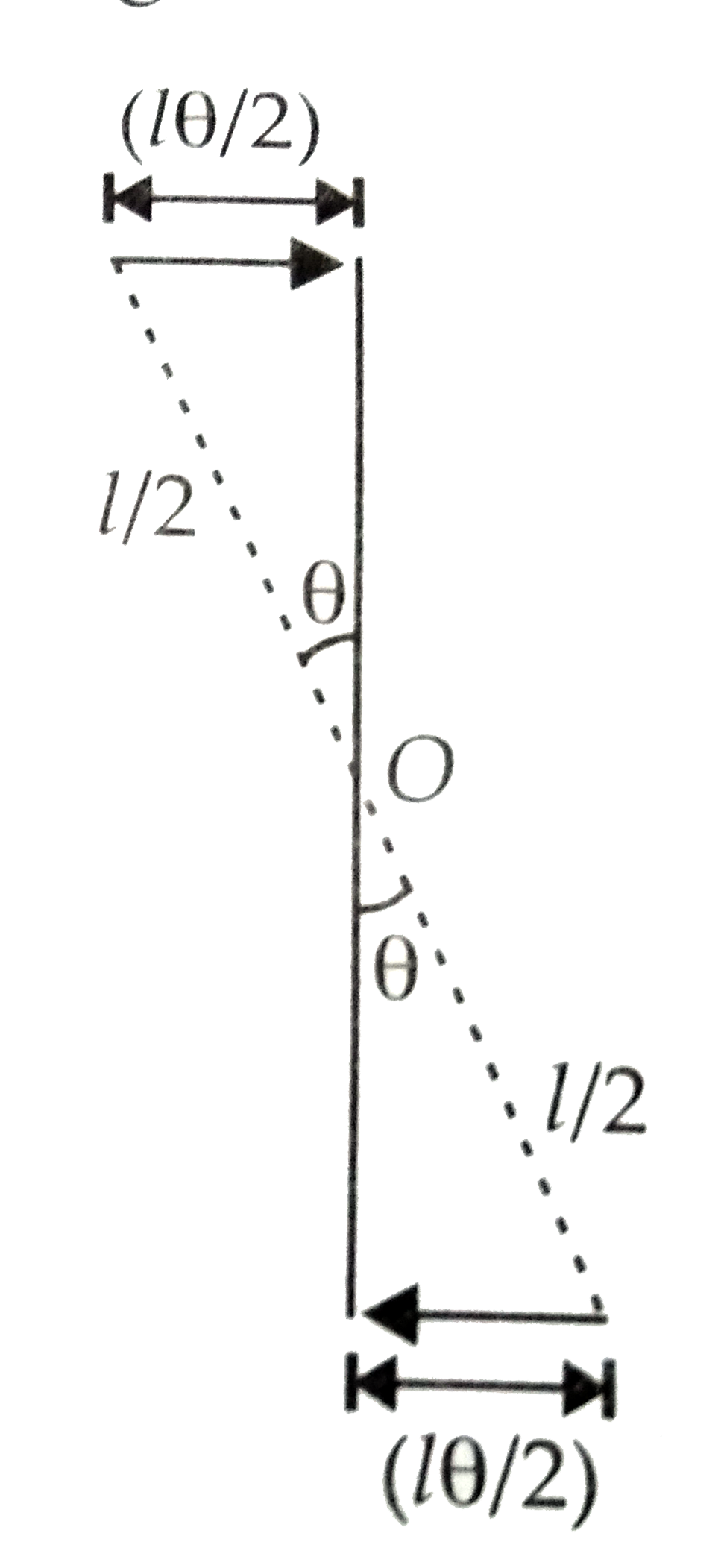
If the rod is rotated through an angle θ, extension in one spring=compression in the other spring,
i.e., x=lθ/2
therefore, force acting on each of
the ends of the rod,
F=kx=k(<hη/2)
Restoring torque on the rod,
τ=−Fl=−k(<hη/2)l=−kl2(θ/2)
As τ=Iα=(Ml2/12)α,
−kl2(θ/2)=(Ml2/12)α
or α=−6kMθ, i.e., α∝θ
thus, the motion of the rod is simple harmonic with
ω2=6kM or ω=√6kM or υ=12π√6kM
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems9videos
OSCILLATIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion & Reason15videos
OSCILLATIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason15videos
OSCILLATIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar6videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason10videos
PHYSICAL WORLD
Similar Questions
two light identical springs of spring constant K are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. the rod is pivoted at its centre 'o' and can rotate freely in horizontal plane . The other ends of the two springs are fixed to rigid supportss as shown in figure . the rod is gently pushed through a small angle and released , the frequency of resulting oscillation is :
 View Solution
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
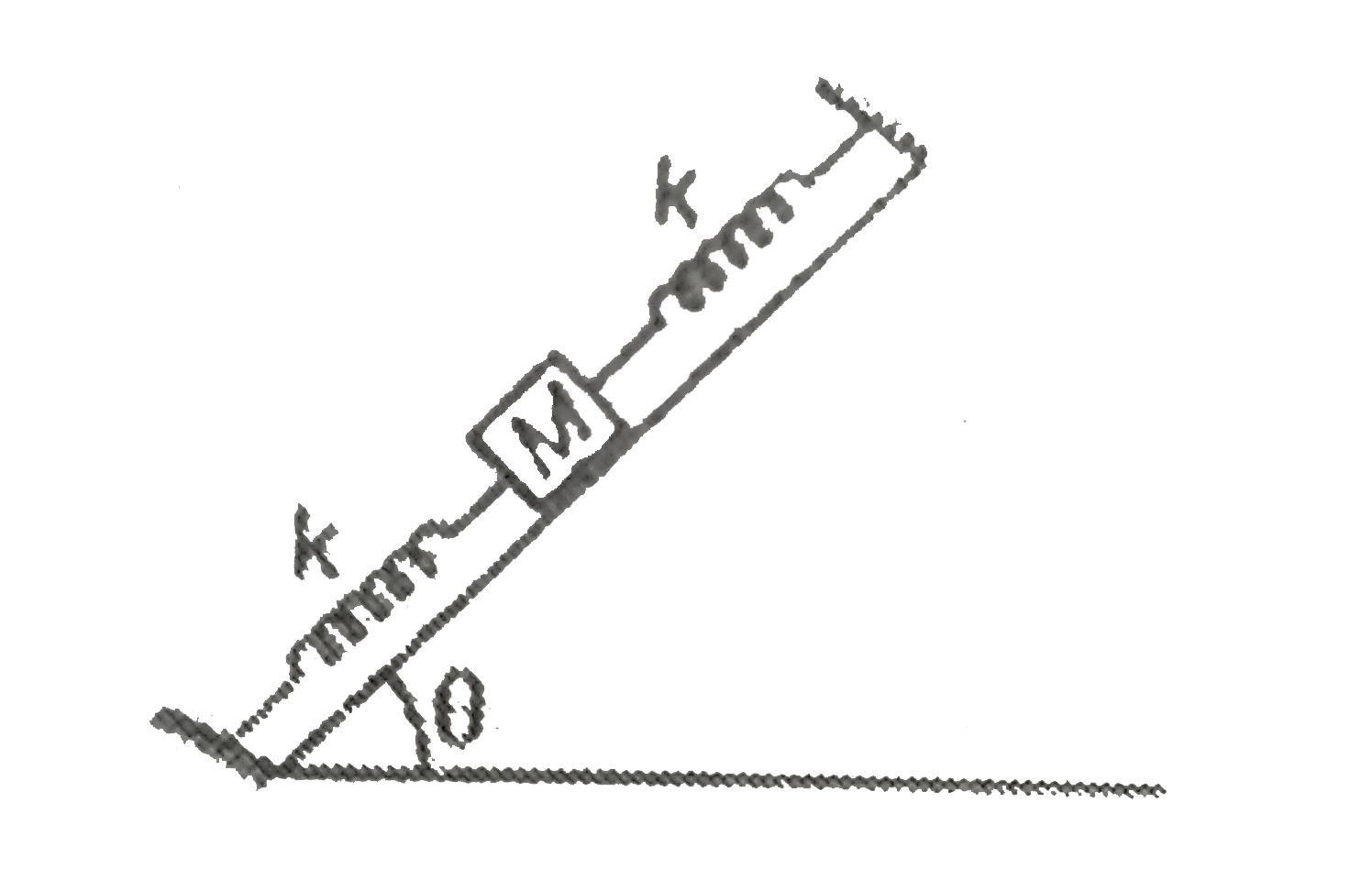
On a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is
 A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
A1. 2π√M2kB2. 2π√2MkC3. 2π√Mgsinθ2kD4. 2π√2Mgk
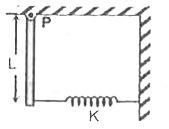
A straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
 View Solution
View SolutionThe ends of a rod of length l and mass m are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre O . The rod is depressed slightly at end A and released . The time period of the oscillation is
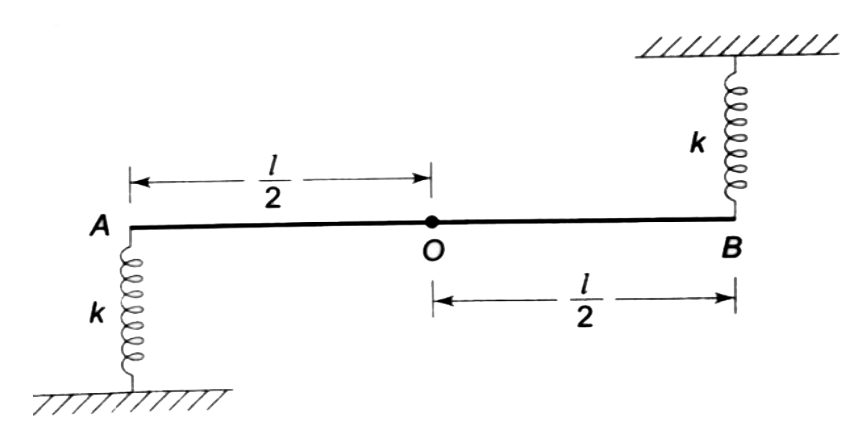 View Solution
View SolutionA thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.
 View Solution
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
 View Solution
View SolutionA mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?
 View Solution
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring one each mass is
View Solution

