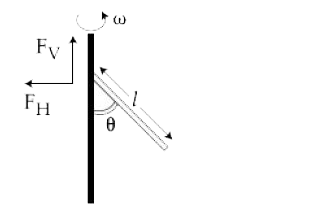
A uniform rod of length 'l' is pivoted at one of itd ends on a vertical shaft of negligible radius When the shaft rotates at angular speed the rod makes an angle with it (see figure) . To find equate the rate of change of angular momentum (direction going into the paper) about the centre of mass (CM) to the torque provided by the horizontal and vertical forces and about the CM. The value of is then such that :
Step by step video & image solution for A uniform rod of length 'l' is pivoted at one of itd ends on a vertical shaft of negligible radius When the shaft rotates at angular speed omega the rod makes an angle theta with it (see figure) . To find theta equate the rate of change of angular momentum (direction going into the paper) (ml^2)/(12) omega^2 sin theta cos theta about the centre of mass (CM) to the torque provided by the horizontal and vertical forces F_H and F_V about the CM. The value of theta is then such that : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at an angle θ with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?
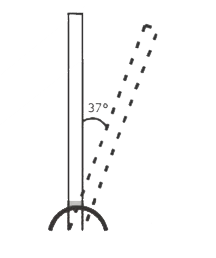
View SolutionA uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
View Solution
Knowledge Check

A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asA√(6gL)sin(θ2)B√(6gL)cos(θ2)C√(6gL)sinθD√(6gL)cosθA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
 Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6A stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
Am(gcosθ+ω2r)Bm√ω4r2+g2Cm√ω2r2+g2Dm(gcosθ−ω2r)
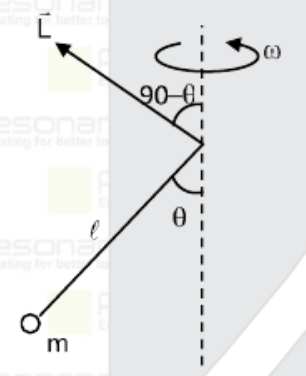
A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
View SolutionA uniform of mass m and length L is tied to a vertical shaft. It rotates in horizontal plane about the vertical axis at angular velocity ω. How much horizontal force does the shaft exert on the rod?

View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.

View SolutionA metallic rod of length L rotates at an angular speed ω, normal to a uniform magnetic field. If the resitance of rod is R the heat dissipated is:
View SolutionA uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is.
 .
.
View Solution
