A uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

For equilibrium
ΣFx=0,ΣFy=0

and Στ=0
For ΣFx=0
f=Nbsinθ………..i
for ΣFy=0
NA+NBcosθ=mg…………….ii
Taking torque of forces about A
NAhsinθ=mgl2cosθ
that gives
NA=mgl2hsinθcosθ .............iii
From eqn ii and iii we get
mgl2hsinθcosθ+NBcosθ=mg
NBcosθ=mg(1−12hsinθcosθ) ...........iv
From eqn i and iv we get
f=m>anθ(1−12hsinθcosθ)........v
But f≤μNA
μ≥Lcosθsin2θ2h−Lcos2θsinθ
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.4
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.2
17 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionA uniform rod of length b can be balanced as shown in figure. The lower end of the rod is resting against a vertical wall. The coefficient of friction between the rod and the wall and that between the rod and the support at A is μ. Distance of support from the wall is a.
(a) Find the ratio ab if the maximum value of θ is θ1.
(b) Find the ratio ab if the minimum value of θ is θ2.
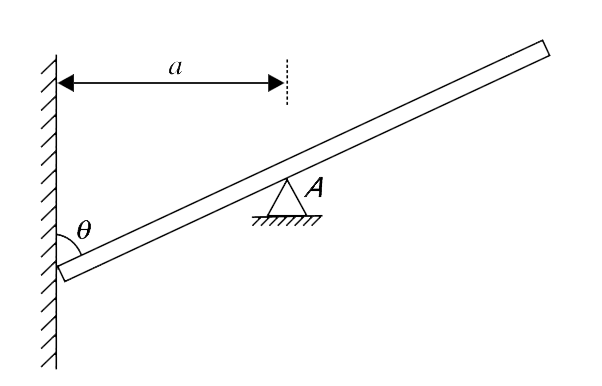
View Solution
Knowledge Check
A ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
Aθ=tan−1(μ)Bθ=tan−1(2μ)Cθ=tan−1(μ2)Dnone of theseA uniform rod AB of length a hangs with one end against a smooth vertical wall, being supported by a string of length l, attached to the other end of the rod and to a point of the rod vertically above B. If the rod rests inclined to the wall at angle θ then cos2θ=
A(l2−a2)/a2B(l2−a2)/2a2C(l2−a2)/3a2Dnone of theseA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.A(√2−1)mgB(√2+1)mgC(√3+1)mgD(√2+3)mg
A uniform rod of length 1m having mass 1kg rests against a smooth wall at an angle of 30∘ with the ground. Calculate the force exerted by the ground on the rod. Take g=10ms−2.
View SolutionA uniform ladder of length l rests against a smooth, vertical wall (figure). If the mass of the ladder is m and the the coefficient of static friction between the ladder and the ground is μs=0.375 and the minimum angle θmin at which the ladder does not slip.

A uniform ladder at rest, leading against a smooth wall. Th ground is rough.
View SolutionA uniform rod is made to lean between a rough vertical wall and the ground. The coefficient of friction between the rod and the ground is μ1 and between the rod and the wall is μ2. Find the angle at which the rod can he leaned without slipping.
View SolutionThere is a fixed half cylinder of radius R on a horizontal table. A uniform rod of length 2R leans against it as shown. At the instant shown, θ=30∘ and the right end of the rod is sliding with velocity v.
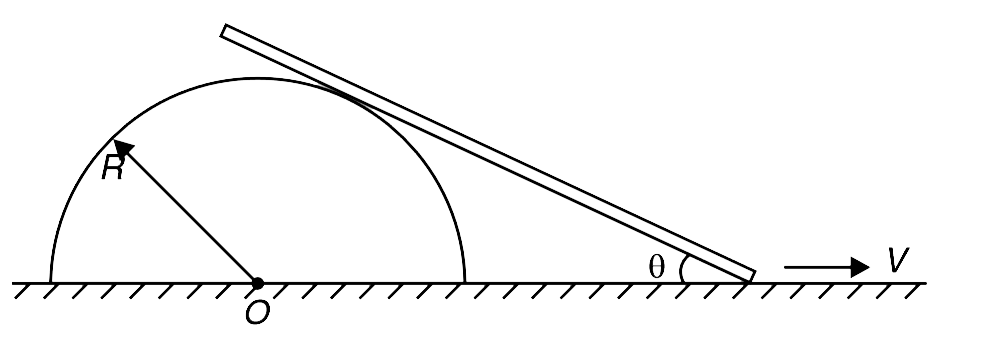
(a) Calculate the angular speed of the rod at this instant.
(b) Find the vertical component of the velocity of the centre of the rod at this instant.
View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the

Normal reaction by ground on the rod
View Solution
