A uniform rod of mass m and length l is released from rest from its vertical position by giving a gently push. In consequence, the end of the rod collides at P after rotating about the smooth horizontal axis O. If the coefficient of restitution e=(12). Find the: a. angular speed of the rod just after the impact.
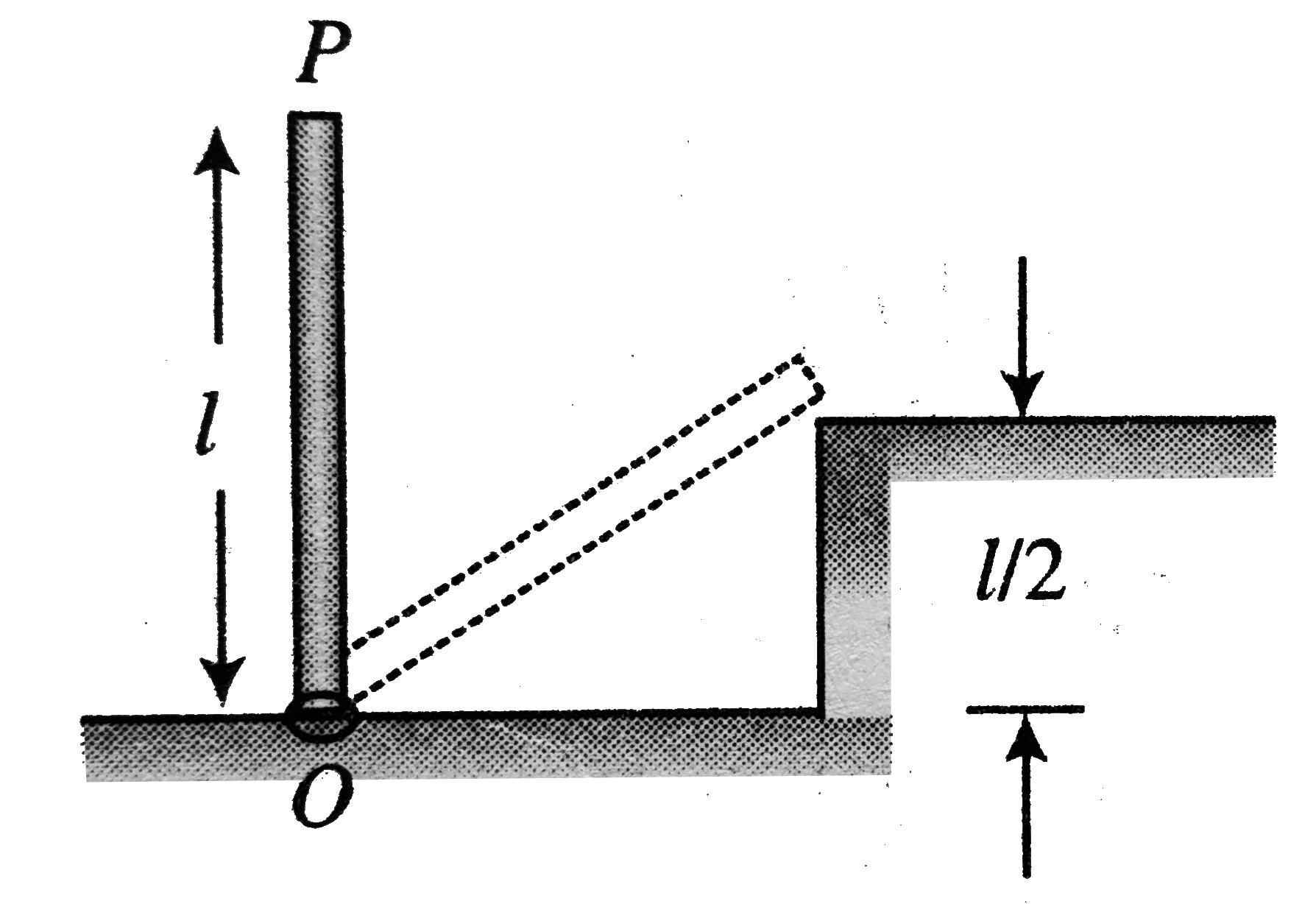
b. energy loss during collision. c. maximum angle rotated collision.
The correct Answer is:58
Since △k=−△U
12(ml23)ω2=mgl2(1−12)
ω=√3g2l
a. The angular speed just after collision is ω'l=eωl
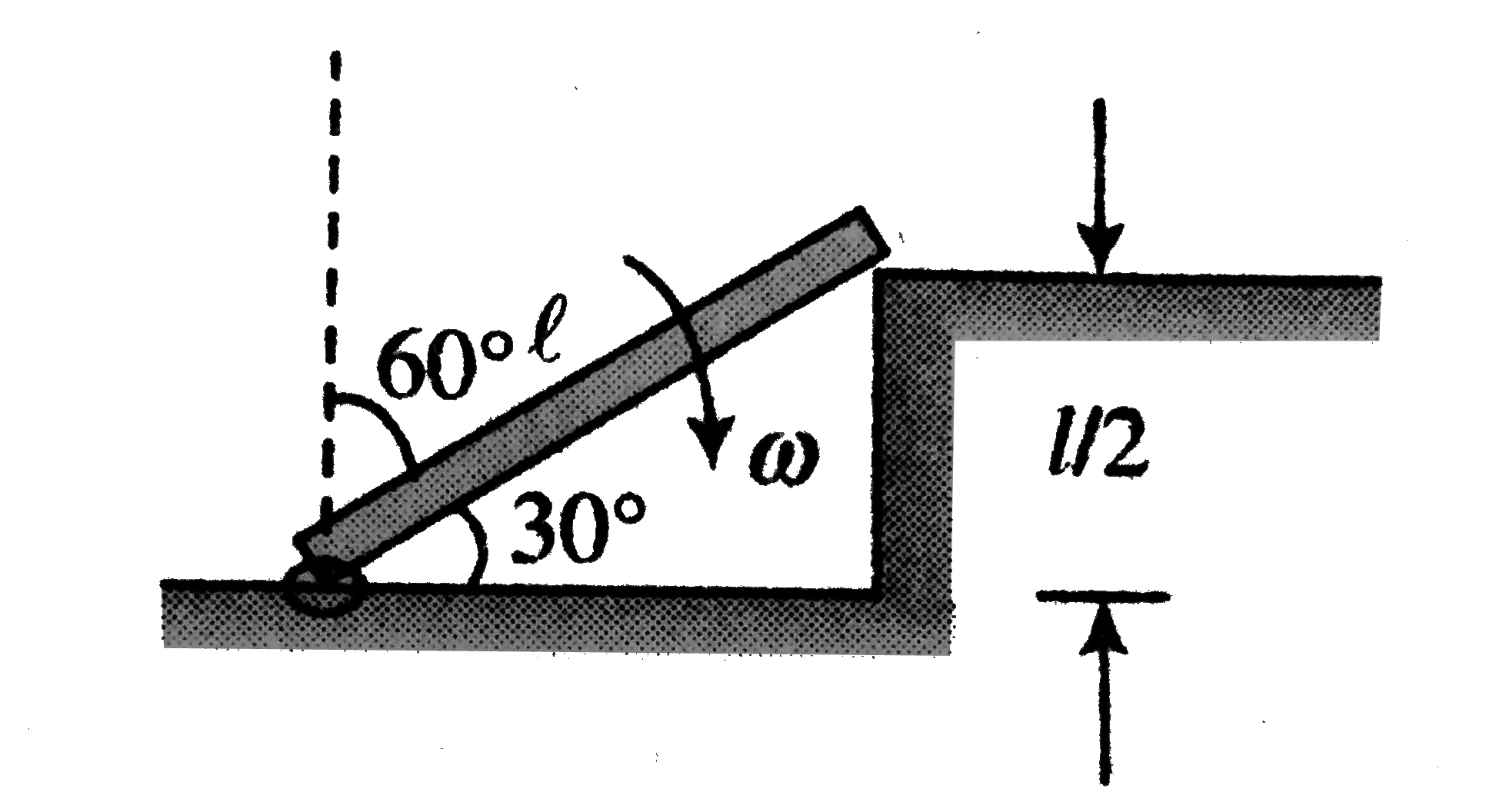
b. △K'=K'−K'=mgl4(1−14)=3mgl16 (∵ω'=ω2)
c. Let the angle rotated be ϕ
△U+△K=0
or mgh−K'=0
or mgh−K'=0

where h=12cosβ−12cos60∘
and K'=mgl6
Then β=cos−158
Hence ϕ=60∘−β=60∘−cos−158
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionA rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View Solution
Knowledge Check
A uniform rod smoothly pivoted at one of its ends is released from rest. If it swings in vertical plane, the maximum speed of the end P of the rod is.
 .A2√3glB√3glC2√2glD√gl
.A2√3glB√3glC2√2glD√glA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
 A15g16B17g16C16g15Dg15
A15g16B17g16C16g15Dg15A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
A uniform rod of mass m and length l is hinged about one of its end. The hinge is smooth and rod lies on a smooth horizontal surface as shown in Fig. A particle of mass m is coming towards the rod at speed v0 perpendicular to the length of rod.
(a) Find angular velocity of the rod just after impact.

(b) Also find impulse due to hinge on rod during collision.
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?

View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.

Distance travelled by the centre of the rod, while rod rotates by 90∘
View Solution
