A uniform semicircular wire is hinged at ‘A’ so that it can rotate freely in vertical plane about a horizontal axis through ‘A’. The semicircle is released from rest when its diameter AB is horizontal Find the hinge force at ‘A’ immediately after the wire is released.
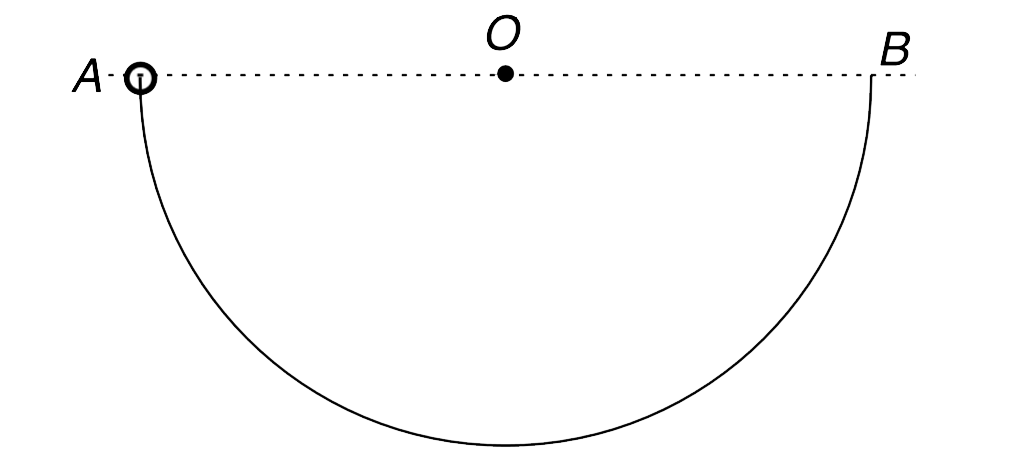
The correct Answer is:Mg√14+1π2
Step by step video, text & image solution for A uniform semicircular wire is hinged at ‘A’ so that it can rotate freely in vertical plane about a horizontal axis through ‘A’. The semicircle is released from rest when its diameter AB is horizontal Find the hinge force at ‘A’ immediately after the wire is released. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View SolutionABC is a triangular framwork of three uniform rods each of mass m and length 2l. It is free to rotate in its own plane about a smooth horizontal axis through A which is perpendicular to ABC. If it is released from rest when AB is horizontal and C is above AB. Find the maximum velocity of C in the subsequent motion.
View Solution
Knowledge Check
A uniform triangular plate ABC of moment of mass m and inertia I (about an axis passing through A and perpendicular to plane of the plate) can rotate freely in the vertical plane about point 'A' as shown in figure. The plate is released from the position shown in the figure. Line AB is horizontal. The acceleration of centre of mass just after the release of plate is
 Amga2√3IBmga24ICmga22√3IDmga23I
Amga2√3IBmga24ICmga22√3IDmga23IThree massless rods are fixed to form a right angled triangular frame such that AB=BC=1 . Two identical small objects of mass m are fixed at A and C . The frame is hinged about B such that the frame can rotate in vertical plane about an horizontal axis without friction. Initially AB is vertical and BC is horizontal and the system is released from rest.
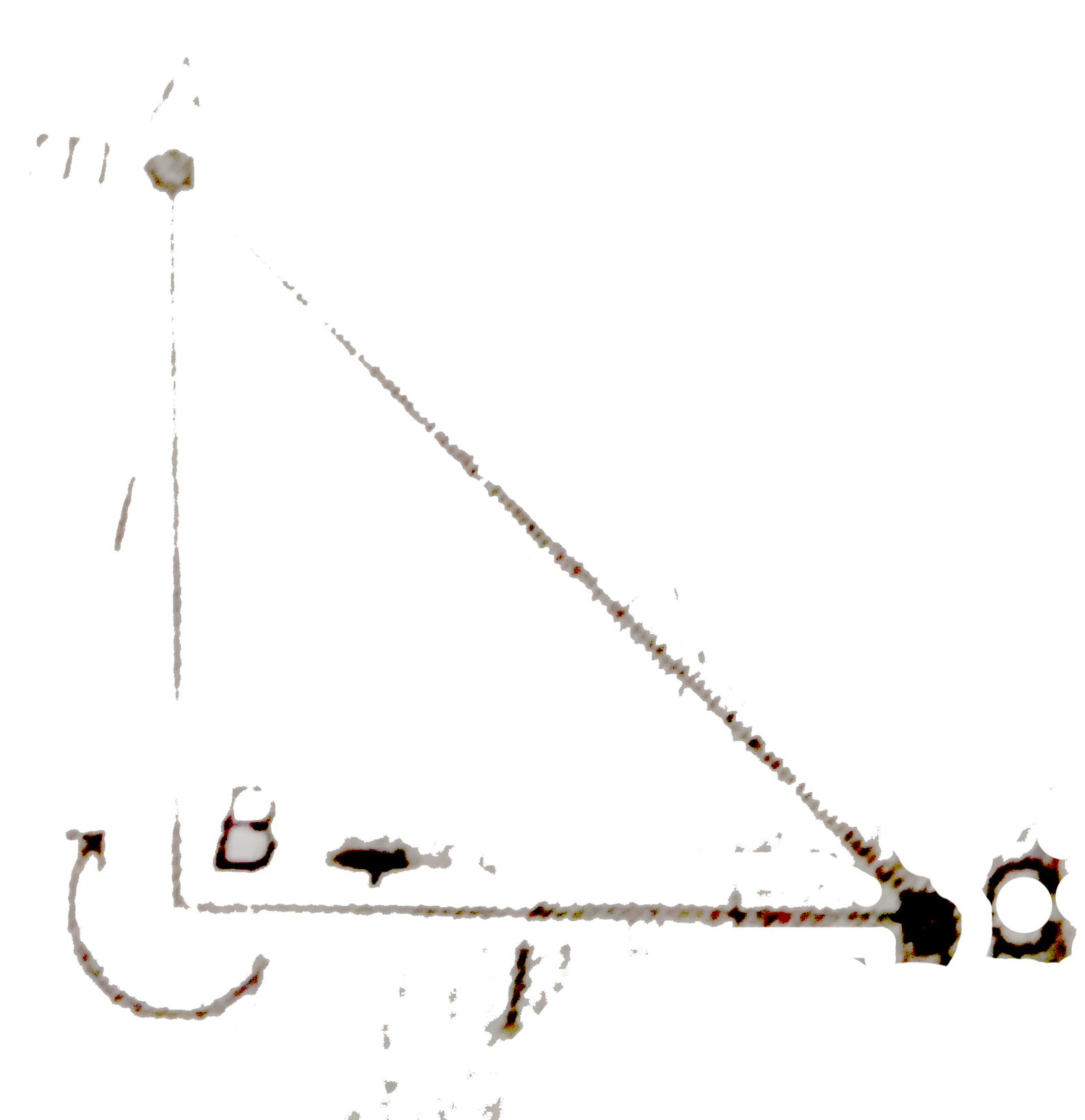
Tension in the rod AC when it (rod AC) becomes horizontal isAmgB√2mgCmg√2D(s√2−1) mgThree massless rods are fixed to form a right angled triangular frame such that AB=BC=1 . Two identical small objects of mass m are fixed at A and C . The frame is hinged about B such that the frame can rotate in vertical plane about an horizontal axis without friction. Initially AB is vertical and BC is horizontal and the system is released from rest.
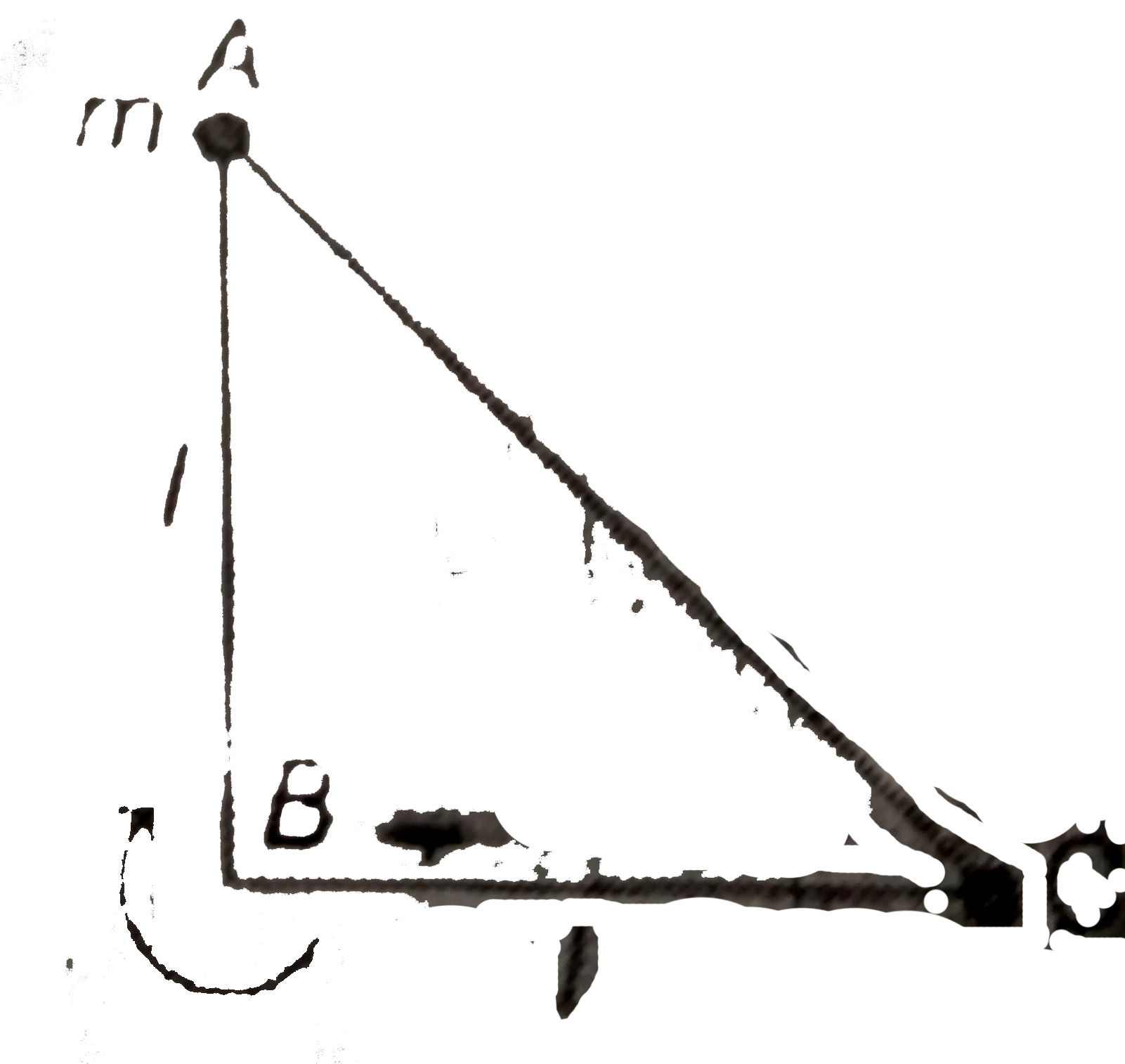
The magnitude of acceleration of mass A when the rod AC becomes horizontal isAg(1+√2)Bg(2+√2)C2g(1+√2)Dg(√2−1)
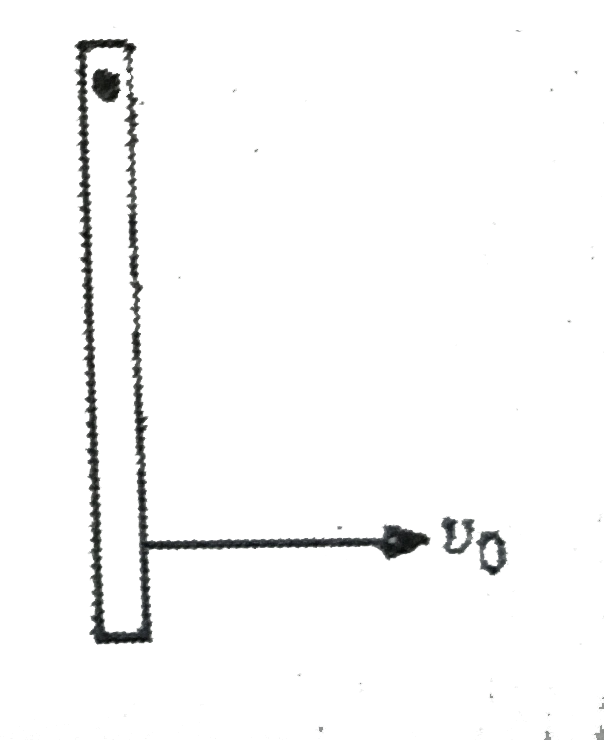
A thin uniform rigid rod of length L is hinged at one end so that it can move in a vertical plane by rotating about a horizontal axis through upper end. The lower end is given a sharp blow and made to acquire a linear velocityvo . Find the maximum height to which the lower end can rise.
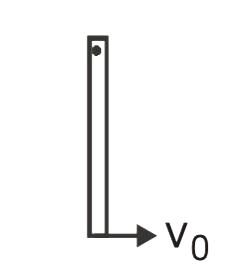
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?

View SolutionThree massless rods are fixed to form a right angled triangular frame such that AB=BC=1 . Two identical small objects of mass m are fixed at A and C . The frame is hinged about B such that the frame can rotate in vertical plane about an horizontal axis without friction. Initially AB is vertical and BC is horizontal and the system is released from rest.
The maximum shift of centre of mass of two mass system from its initial position is
View SolutionA thin uniform rigid rod of length l is hinged at one end so that it can move ina vertical plane by rotating about a horizontal axis through upper end. The lower end is given a sharp blow and made to acquire a linear velocity Maximum height attained by lower end of the rod is:
View SolutionA uniform disc of mass M and radius R is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
View Solution
