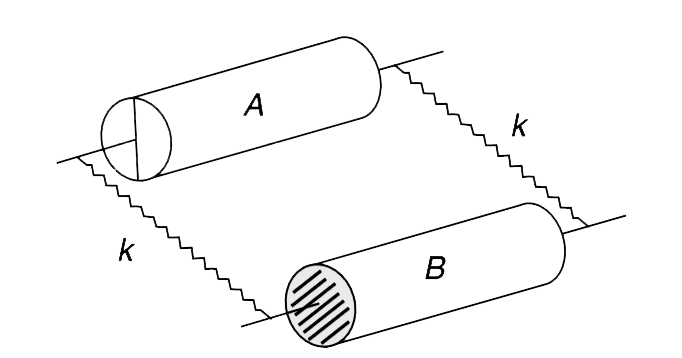
A hollow cylindrical pipe A has mass M and radius R. With the help of two identical springs (each of force constant k) it is connected to solid cylinder B having mass M and radius R. The springs are connected symmetrically to the axle of the cylinders. Moment of inertia of the two Bodies A and B about their axles are IA=MR2 and IB=12MR2 respectively. Cylinders are pulled apart so as to stretch the springs by x0 and released. During subsequent motion the cylinders do not slip.
(a) Find acceleration of the centre of mass of the system immediately after it is released.
(b) Find the distance travelled by cylinder A by the time it comes to rest for the first time after being released.
The correct Answer is:(a) kx06M
(b) (6x_(0))/(7)
Step by step video, text & image solution for A hollow cylindrical pipe A has mass M and radius R. With the help of two identical springs (each of force constant k) it is connected to solid cylinder B having mass M and radius R. The springs are connected symmetrically to the axle of the cylinders. Moment of inertia of the two Bodies A and B about their axles are I_(A) = MR^(2) and I_(B) = (1)/(2) MR^(2) respectively. Cylinders are pulled apart so as to stretch the springs by x0 and released. During subsequent motion the cylinders do not slip. (a) Find acceleration of the centre of mass of the system immediately after it is released. (b) Find the distance travelled by cylinder A by the time it comes to rest for the first time after being released. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Let →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .03:21View SolutionTwo particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time
 05:53View Solution
05:53View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
02:41View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
02:50View SolutionWhat is moment of inertia of a solid cylinder of mass m, length l and radiusr about the axis of the cylinder ?
01:38View SolutionMoment of inertia of a hollow cylinder of mass M and radius R , about the axis of cylinder is
02:50View SolutionA ring and a thin hollow cylinder have the same mass and radius. If Ir and Is represent their moment of inertia about their axes, then
04:10View SolutionTwo solid spheres A and B each of radius R are made of materials of densities P_(A) and P_(B) respectively. Their moments of inertia about a diameter are I_(A) and I_(B) respectively. The value of I_(A)//I_(B) is
06:55View SolutionCalculate the moment of inertia of a hollow cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder?
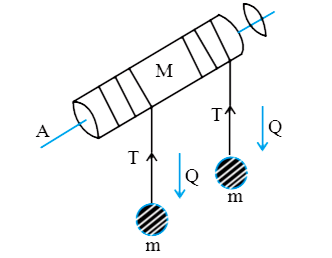
05:13View SolutionA uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
 02:32View Solution
02:32View SolutionMoment of inertia of a hollow cylinder of mass M and radius r about its own axis is
04:52View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
04:52View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
05:55View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
03:08View Solution

