A uniform smooth rod (mass m and length l) placed on a smooth horizontal floor is it by a particle (mass m) moving on the floor, at a distance l4 from one end elastically (e=1). The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
2πl
cannot be determined
πl
none of the above
The correct Answer is:A
To solve the problem step by step, we can follow these steps:
Step 1: Understand the Setup
We have a uniform smooth rod of mass m and length l placed on a smooth horizontal floor. A particle of mass m hits the rod at a distance of l4 from one end. The collision is elastic, meaning both momentum and kinetic energy are conserved.
Step 2: Determine the Impulse and Angular Impulse
When the particle collides with the rod, it exerts an impulse on the rod. The impulse can be expressed as:
\( I = m \cdot v_0 \)
where \( v_0 \) is the initial velocity of the particle before the collision.
The angular impulse about the center of mass of the rod is given by:
\( \text{Angular Impulse} = I \cdot \text{distance from center} \)
The distance from the center of the rod to the point of impact is \( l/4 \) (since the center is at \( l/2 \) and the impact point is at \( l/4 \)):
\( \text{Angular Impulse} = I \cdot \left(\frac{l}{4}\right) \)
Step 3: Relate Linear and Angular Quantities
The angular impulse can also be expressed in terms of the final angular velocity \( \omega_f \) of the rod:
\( I \cdot \frac{l}{4} = I_{cm} \cdot \omega_f \)
where \( I_{cm} \) is the moment of inertia of the rod about its center of mass, given by:
\( I_{cm} = \frac{1}{12} m l^2 \)
Step 4: Calculate the Final Angular Velocity
From the angular impulse equation, we can solve for \( \omega_f \):
\( I \cdot \frac{l}{4} = \frac{1}{12} m l^2 \cdot \omega_f \)
Substituting \( I = m v_0 \):
\( m v_0 \cdot \frac{l}{4} = \frac{1}{12} m l^2 \cdot \omega_f \)
Cancelling \( m \) from both sides:
\( v_0 \cdot \frac{l}{4} = \frac{1}{12} l^2 \cdot \omega_f \)
Rearranging gives:
\( \omega_f = \frac{3 v_0}{l} \)
Step 5: Calculate the Time to Complete Three Revolutions
The angle rotated in three revolutions is:
\( \theta = 3 \cdot 2\pi = 6\pi \)
Using the relationship between angular displacement, angular velocity, and time:
\( \theta = \omega_f \cdot t \)
Substituting for \( \omega_f \):
\( 6\pi = \left(\frac{3 v_0}{l}\right) t \)
Solving for \( t \):
\( t = \frac{6\pi l}{3 v_0} = \frac{2\pi l}{v_0} \)
Step 6: Calculate the Distance Traveled by the Center of the Rod
The distance traveled by the center of the rod while it completes three revolutions is given by:
\( \text{Distance} = v_{cm} \cdot t \)
Where \( v_{cm} \) is the velocity of the center of mass of the rod after the collision. The velocity of the center of mass can be found using:
\( v_{cm} = \frac{v_0}{2} \)
Thus, the distance traveled is:
\( \text{Distance} = \frac{v_0}{2} \cdot \frac{2\pi l}{v_0} = \pi l \)
Final Answer
The distance traveled by the center of the rod after it has completed three revolutions is:
\( \text{Distance} = \pi l \)
---
We have a uniform smooth rod of mass m and length l placed on a smooth horizontal floor. A particle of mass m hits the rod at a distance of l4 from one end. The collision is elastic, meaning both momentum and kinetic energy are conserved.
When the particle collides with the rod, it exerts an impulse on the rod. The impulse can be expressed as:
\( I = m \cdot v_0 \)
where \( v_0 \) is the initial velocity of the particle before the collision.
\( \text{Angular Impulse} = I \cdot \text{distance from center} \)
The distance from the center of the rod to the point of impact is \( l/4 \) (since the center is at \( l/2 \) and the impact point is at \( l/4 \)):
\( \text{Angular Impulse} = I \cdot \left(\frac{l}{4}\right) \)
The angular impulse can also be expressed in terms of the final angular velocity \( \omega_f \) of the rod:
\( I \cdot \frac{l}{4} = I_{cm} \cdot \omega_f \)
where \( I_{cm} \) is the moment of inertia of the rod about its center of mass, given by:
\( I_{cm} = \frac{1}{12} m l^2 \)
From the angular impulse equation, we can solve for \( \omega_f \):
\( I \cdot \frac{l}{4} = \frac{1}{12} m l^2 \cdot \omega_f \)
Substituting \( I = m v_0 \):
\( m v_0 \cdot \frac{l}{4} = \frac{1}{12} m l^2 \cdot \omega_f \)
Cancelling \( m \) from both sides:
\( v_0 \cdot \frac{l}{4} = \frac{1}{12} l^2 \cdot \omega_f \)
Rearranging gives:
\( \omega_f = \frac{3 v_0}{l} \)
The angle rotated in three revolutions is:
\( \theta = 3 \cdot 2\pi = 6\pi \)
Using the relationship between angular displacement, angular velocity, and time:
\( \theta = \omega_f \cdot t \)
Substituting for \( \omega_f \):
\( 6\pi = \left(\frac{3 v_0}{l}\right) t \)
Solving for \( t \):
\( t = \frac{6\pi l}{3 v_0} = \frac{2\pi l}{v_0} \)
The distance traveled by the center of the rod while it completes three revolutions is given by:
\( \text{Distance} = v_{cm} \cdot t \)
Where \( v_{cm} \) is the velocity of the center of mass of the rod after the collision. The velocity of the center of mass can be found using:
\( v_{cm} = \frac{v_0}{2} \)
Thus, the distance traveled is:
\( \text{Distance} = \frac{v_0}{2} \cdot \frac{2\pi l}{v_0} = \pi l \)
The distance traveled by the center of the rod after it has completed three revolutions is:
\( \text{Distance} = \pi l \)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
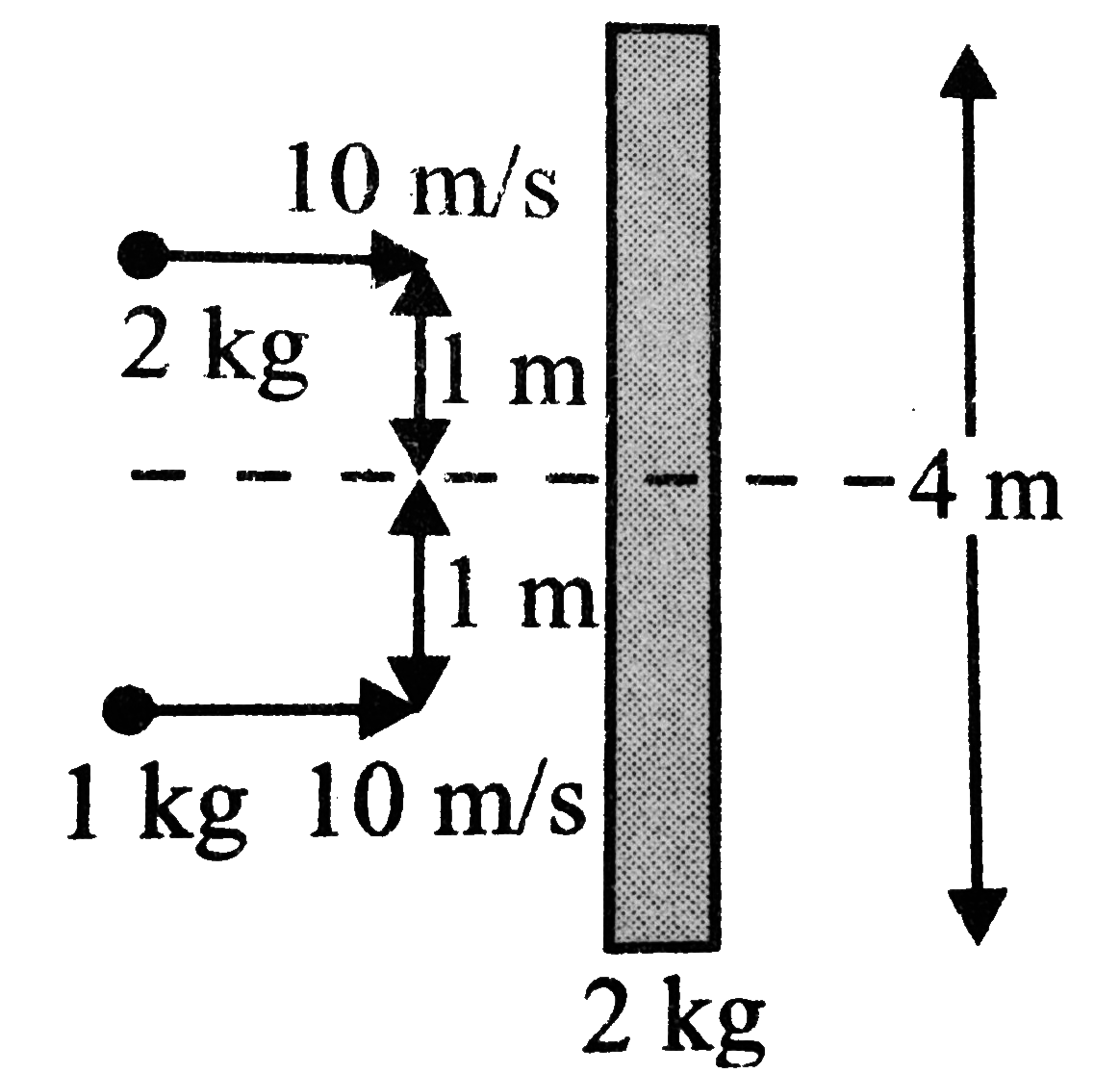
Velocity of the centre of mass of the rod after collision isView SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
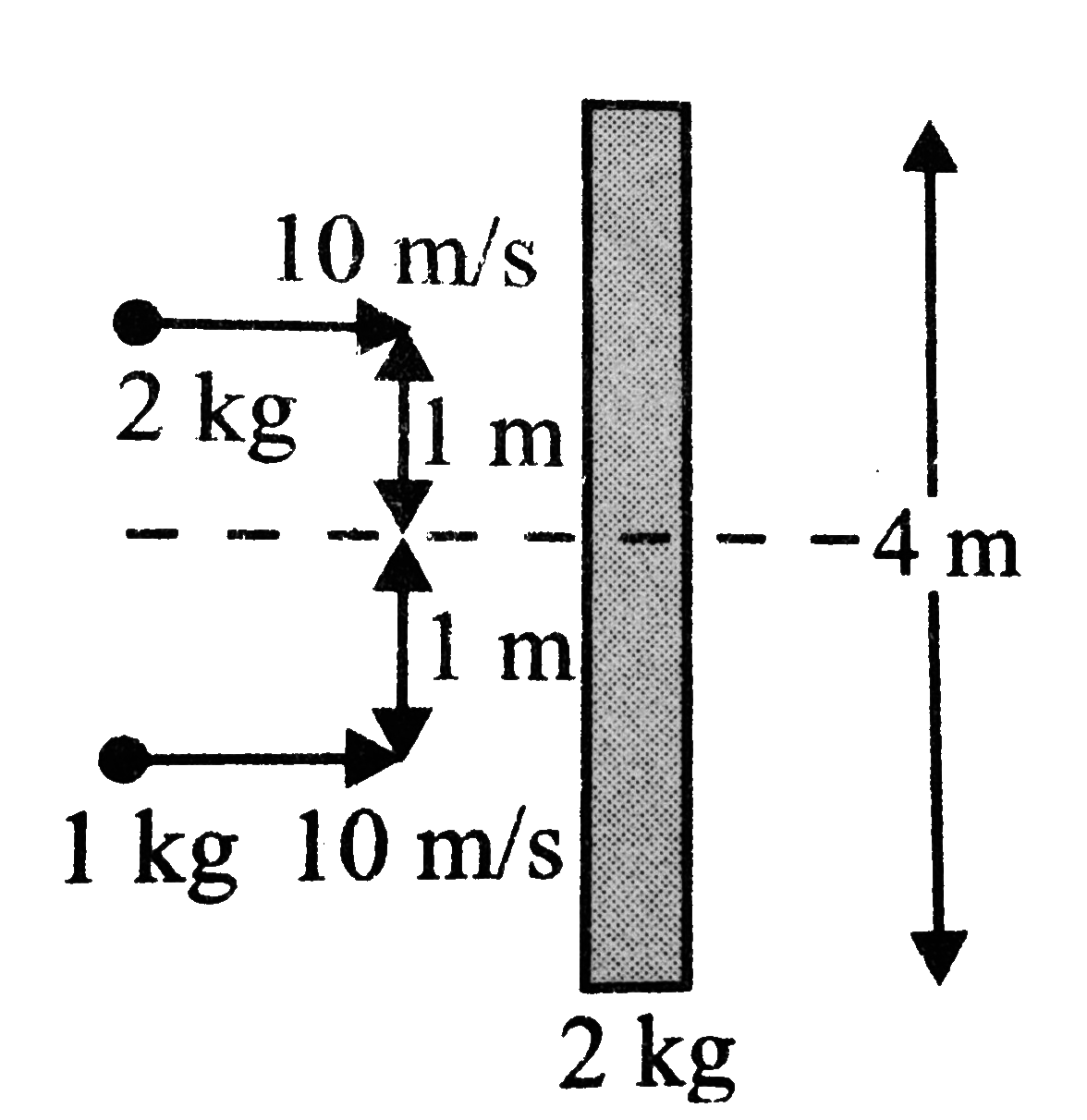
Angular velocity of the rod after collision isView SolutionA uniform rod of mass 2kg and length 1m lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of 2ms−1 perpendicular to the length of the rod strikes it at a distance 14 m from the centre and stops . Find the angular velocity of the rod about its centre just after the collision (in rad/s)
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 View Solution
View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :View Solution
