A uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.
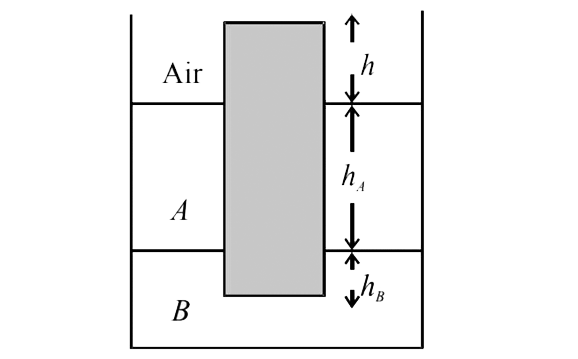
(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.
a. Liquid A exerts horizotal force on all area elements for all directions. By symmetry, the resultant of these horizontal force is zero. So the total force exerted by liquid A onn the cylinder is zero.
b. Let A be the cross sectional area of the cylinder.
For floating equilibrium.
Weight of floating cylinder = Buoyant force = weight of liqid displaced.
(h+hA+hB)×A×0.8g=(hAρAg+hBAρBg)
or (h+hA+hB)×0.8=hAρA+hBρB
⇒(h+1.2+0.8)×=1.2×0.7+0.8×1.2
⇒0.8h+1.6=1.8or0.8h=0.2
⇒h=0.25cm
b. Mass of cylilnder =(h+hA+hB)Aρ
=(0.2+1.2+0.8)A×0.8=1.8A
When the cylinder is depressed just completely, its height h goes in liquid B, so extra buoyant fore due to liquid B acts on it. Due to this force cylinder is accelerated upward.
Extra buoyant force F=(hA)ρBg
=0.25A×1.2g=0.3Ag
Acceleration is given by a=Fm=0.3Agm=0.3Ag1.8A=g6
=106=53m/s2
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.2
11 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A solid cylinder of length L is in equilibrium in two different liquid A and B as shown in the figure.The density of liquid A 3ρ2 and liquid B is 3ρ.The density of cylinder is
View SolutionA column of water 40cm high supports a 30cm column of an unknown liquid . What is the density of the liquid ?
View SolutionTwo miscible liquids of densities 1.2gm/cm and 1.4gm/cm aer mixed with a proportion ratio of their volumes equal to 2.5: what is the density of redulting liquid?
View SolutionTwo immiscible of densities 2.5g/cm3 and 0.8g/cm3 are taken in the ratio of their masses as 2:3 respectively find the average density of the liquid conbination.
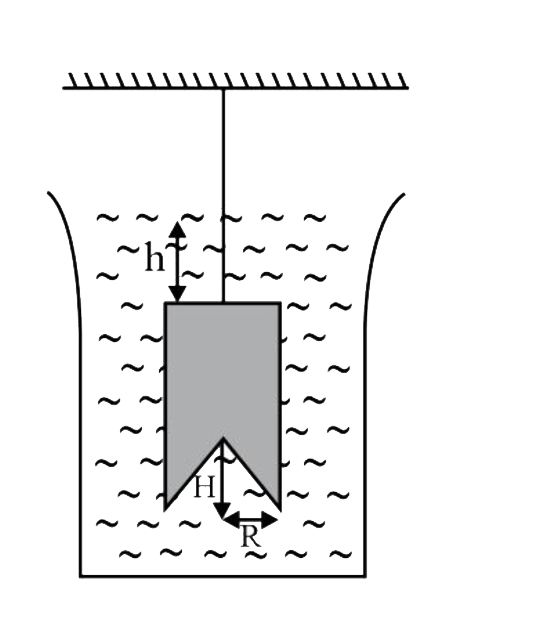
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
View SolutionA body is volume 100cm3 weighs 5 kgf in air. It is completely immersed in a liquid of density 1.8×103kgm−3. Find (i) the upthrust due to liquid and (ii) the weight of the body in liquid.
View SolutionTwo solids A and B of density 2.5 g cm−3 and 0.80g cm−3 are placed in a liquid L of density 1.2 g cm−3 Which solid is likely to float and why?
View SolutionTwo immiscible liquid of densities rho and 3ρ are put in a container. The height of each liquid is h. A solid cylinder of length L and density d is put in this container. The cylinder floats completely inside liquids with its axis vertical and length L3 in the denser liquid. The density d is equal to
View SolutionA cube of side 4 cm is just completely immersed in a liquid A. When it is put in a liquid B, it floats with 2 cm outside the liquid. Calculate the ratio of densities of the two liquids.
View SolutionA body of density 2.5g/cm3 is let free in a liquid of density 1.25g/cm3 . The downward acceleration of the of the body while sinking in the liquid is . _______
View Solution
