A uniform thin flat isolated disc is floating in space. It has radius R and mass m . A force is applied to it at a distance d=(R2) from the centre in the y-direction. Treat this problem as two-dimensional. Just after the force is applied:
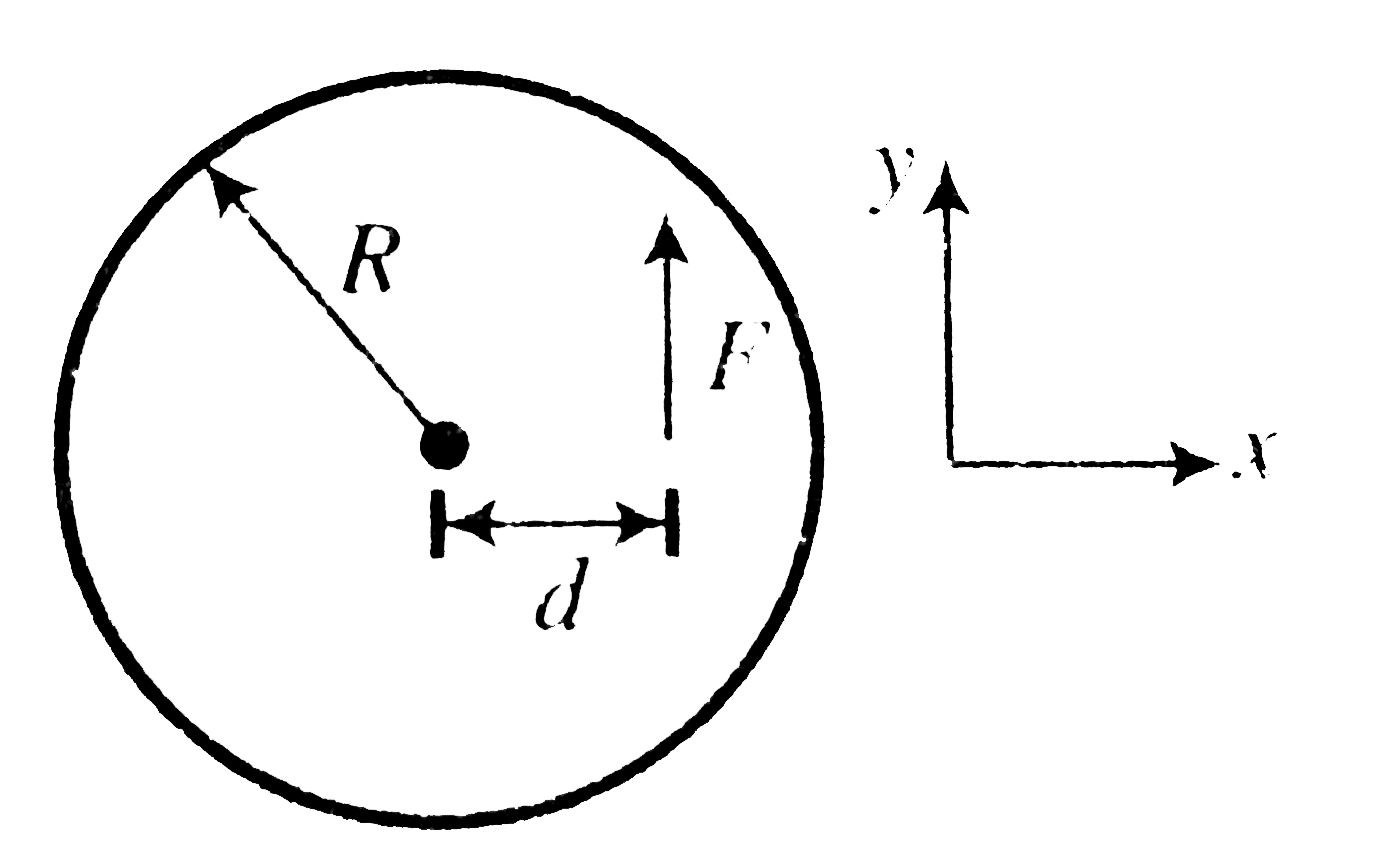
acceleration of the centre of the disc is F/m.
angular acceleration of the disk is F/mR.
acceleration of leftmost point on the, disc is zero
point which is instantaneously unaccelerated is the rightmost point.
The correct Answer is:A, B, C
F=ma……….i

FR2=12mR2α…………ii
aP=a−αR=0
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct
97 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA uniform rod of mass M=2kg and length L is suspended by two smooth hinges 1 and 2 as shown in Fig. A force F=4N is applied downward at a distance L/4 from hinge 2. Due to the application of force F, hinge 2 breaks. At this instant, applied force F is also removed. The rod starts to rotate downward about hinge 1. (g=10m/s2)

The reaction at hinge 1, just after breaking of hinge 2, is
View Solution
Knowledge Check
A point mass m is placed inside a spherical shell of radius R and mass M at a distance R2 form the centre of the shell. The gravitational force exerted by the shell on the point mass is
AGMmR2B2GMmR2CzeroD4MmR2A mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass m is
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2
A cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
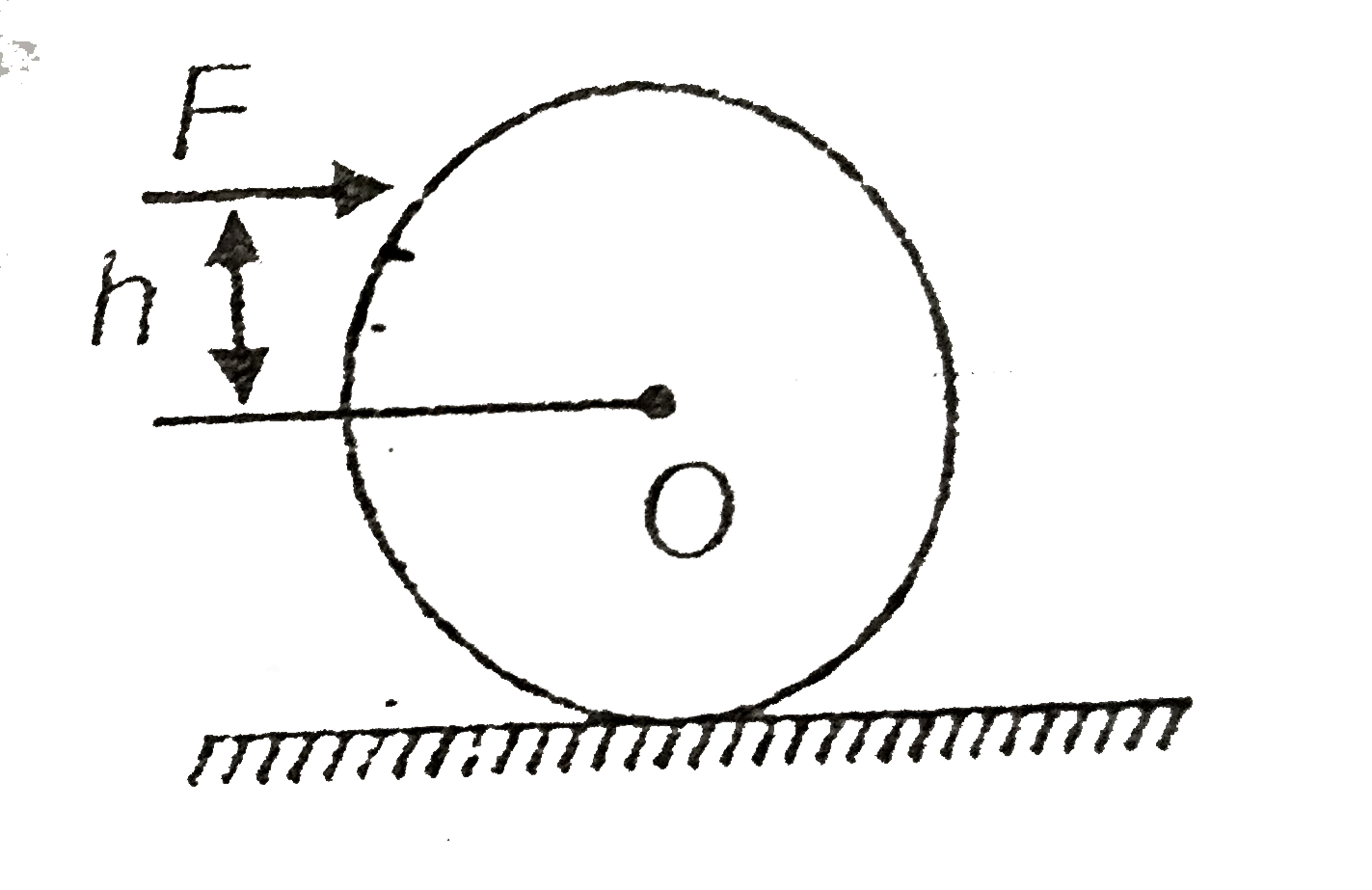
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View Solution
