A bucket of water of mass 21kg is suspended by a rope wrapped around a solid cylinder 0.2m in diameter. The mass of the solid cylinder is 21kg. The bucket is released from rest. Which of the following statements are correct?
The tension in the rope is 70N.
The acceleration of the bucket is (203)m/s2
The acceleration of the bucket is independent of the mass of the bucket.
All of these
The correct Answer is:A, B, C, D
To solve the problem step by step, we will analyze the forces acting on the bucket and the torque acting on the solid cylinder.
Step 1: Identify the Forces Acting on the Bucket
The forces acting on the bucket are:
- The gravitational force (weight) acting downward: Fg=mg=21kg×g (where g≈9.81m/s2)
- The tension T in the rope acting upward.
Step 2: Write the Equation of Motion for the Bucket
Using Newton's second law, we can write the equation for the bucket:
mg−T=ma
Substituting m=21kg:
21g−T=21a(1)
Step 3: Analyze the Solid Cylinder
The rope wrapped around the solid cylinder creates a torque τ on the cylinder. The torque is given by:
τ=T⋅R
where R is the radius of the cylinder. Since the diameter is 0.2m, the radius R=0.1m.
Step 4: Write the Torque Equation
The torque is also related to the angular acceleration α of the cylinder:
τ=Iα
where I is the moment of inertia of the solid cylinder. For a solid cylinder, the moment of inertia is:
I=12mR2=12×21kg×(0.1m)2=21×0.012=0.105kg m2
Step 5: Relate Linear and Angular Acceleration
The linear acceleration a of the bucket is related to the angular acceleration α of the cylinder by:
a=Rα⟹α=aR
Substituting this into the torque equation gives:
T⋅R=I⋅aR
Rearranging gives:
T=I⋅aR2(2)
Step 6: Substitute for I
Substituting I=0.105kg m2 and R=0.1m into equation (2):
T=0.105⋅a(0.1)2=0.105⋅a0.01=10.5a
Step 7: Substitute T Back into Equation (1)
Substituting T=10.5a into equation (1):
21g−10.5a=21a
Rearranging gives:
21g=21a+10.5a=31.5a⟹a=21g31.5
Step 8: Calculate the Acceleration
Substituting g≈9.81m/s2:
a=21×9.8131.5≈205.0131.5≈6.5m/s2
Step 9: Calculate the Tension
Using a to find T:
T=10.5⋅a=10.5⋅6.5≈68.25N
Conclusion
After analyzing the forces and calculating the acceleration and tension, we can conclude that:
- The acceleration of the bucket is approximately 6.5m/s2.
- The tension in the rope is approximately 68.25N.
The forces acting on the bucket are:
- The gravitational force (weight) acting downward: Fg=mg=21kg×g (where g≈9.81m/s2)
- The tension T in the rope acting upward.
Using Newton's second law, we can write the equation for the bucket:
mg−T=ma
Substituting m=21kg:
21g−T=21a(1)
The rope wrapped around the solid cylinder creates a torque τ on the cylinder. The torque is given by:
τ=T⋅R
where R is the radius of the cylinder. Since the diameter is 0.2m, the radius R=0.1m.
The torque is also related to the angular acceleration α of the cylinder:
τ=Iα
where I is the moment of inertia of the solid cylinder. For a solid cylinder, the moment of inertia is:
I=12mR2=12×21kg×(0.1m)2=21×0.012=0.105kg m2
The linear acceleration a of the bucket is related to the angular acceleration α of the cylinder by:
a=Rα⟹α=aR
Substituting this into the torque equation gives:
T⋅R=I⋅aR
Rearranging gives:
T=I⋅aR2(2)
Substituting I=0.105kg m2 and R=0.1m into equation (2):
T=0.105⋅a(0.1)2=0.105⋅a0.01=10.5a
Substituting T=10.5a into equation (1):
21g−10.5a=21a
Rearranging gives:
21g=21a+10.5a=31.5a⟹a=21g31.5
Substituting g≈9.81m/s2:
a=21×9.8131.5≈205.0131.5≈6.5m/s2
Using a to find T:
T=10.5⋅a=10.5⋅6.5≈68.25N
After analyzing the forces and calculating the acceleration and tension, we can conclude that:
- The acceleration of the bucket is approximately 6.5m/s2.
- The tension in the rope is approximately 68.25N.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension28videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct97videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A bucket of mass 8 kg is supported by a light rope wound around a solid wooden cylinder of mass 12 kg and radius 20 cm free to rotate about its axis. A man holding the free end of the rope, with the bucket and the cylinder at rest initially, lets go the bucket freely downwards in a well 50 m deep. Neglecting friction, obtain the speed of the bucket and the angular speed of the cylihder just before the bucket enters water.
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.
 View Solution
View SolutionTwo discs A and B each of mass 2kg and radius 0.5m are rigidly fixed to the end of a thin shaft S, which is supported in horizontal position with the help of two smooth bearings at points P1 and P2. Two blocks of masses 2kg and 1kg are connected to the light cords wrapped around the discs as shown in the figure. There is no slipping between the cord and the discs. If the system is released from rest from the position shown, the mark released from rest from the position shown,
 View Solution
View SolutionOn the surface of a solid cylinder of mass 2 kg and radius 25 cm a string is wound several times and the end of the string is held stationary while the cylinder is released from rest. What is the acceleration of the cylinder and the tension in the string ?
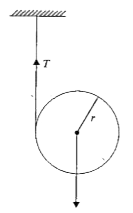 View Solution
View SolutionA solid cyinder of mass m=4kg and radius R=10cm has two ropes wrapped around it. one near each end. The cylinder is held horizontally by fixing the two free ends of the cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the linear acceleration of the cylinder.
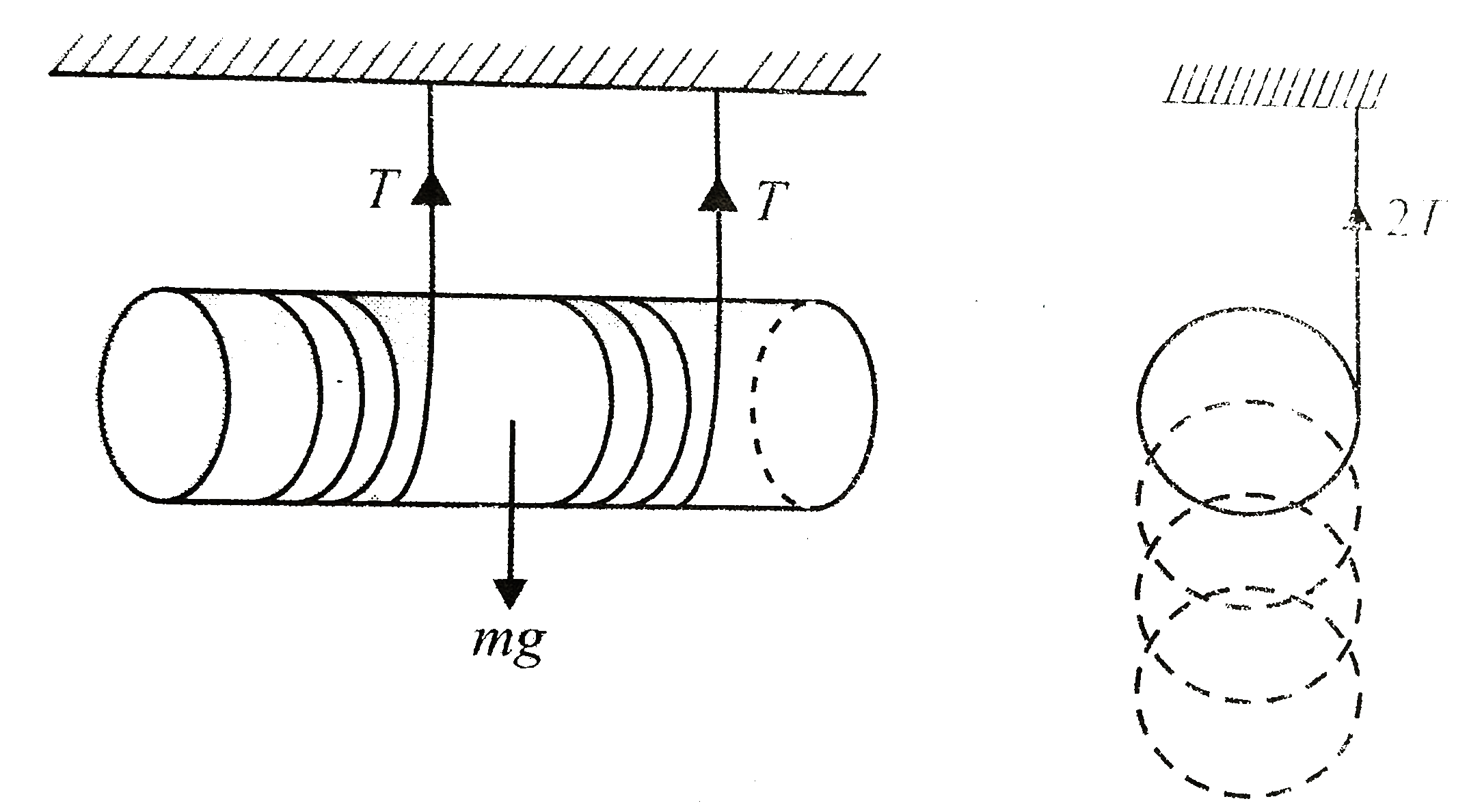 View Solution
View SolutionThe mass of the cylinder is 25 kg and radius of cylinder is 5 m. Find the moment of inertia of a solid cylinder about a tangent to the cylinder.
View SolutionA rope is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30N ?
View SolutionA rope is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30N ?
View SolutionA uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
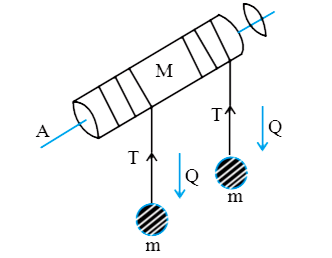 View Solution
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View Solution

