A uniform tube closed at aone end, contains a pellet of mercury 10cm long. When the tube is lept vertically with the closed-end upward, the length of the air column trapped is 20cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure=75cm of mercury.
To solve the problem, we need to analyze the situation using the ideal gas law and the concept of pressure in a closed system. Let's break it down step by step.
Step 1: Understand the Initial Conditions
Initially, the tube is closed at one end and has a mercury pellet of length 10 cm. The air column trapped in the tube is 20 cm long. The atmospheric pressure is given as 75 cm of mercury (cmHg).
Step 2: Calculate the Initial Pressure of the Air Column (P1)
When the tube is upright (closed end up), the pressure exerted by the trapped air (P1) can be calculated using the atmospheric pressure and the height of the mercury column:
P1=Patm−PHg
Where:
- Patm=75cmHg
- PHg=10cmHg (the height of the mercury column)
Thus,
P1=75cmHg−10cmHg=65cmHg
Step 3: Calculate the Volume of the Air Column (V1)
The volume of the air column (V1) can be expressed in terms of the length of the air column (20 cm) and the cross-sectional area (A) of the tube:
V1=A×20cm
Step 4: Set Up the Conditions for the Inverted Tube
When the tube is inverted (closed end down), the length of the air column is unknown (let's call it x). The pressure (P2) in this case is the atmospheric pressure plus the pressure due to the mercury column:
P2=Patm+PHg=75cmHg+10cmHg=85cmHg
Step 5: Calculate the Volume of the Air Column (V2)
The volume of the air column (V2) when the tube is inverted can be expressed as:
V2=A×x
Step 6: Apply the Ideal Gas Law
According to the ideal gas law, the product of pressure and volume remains constant (assuming temperature and the number of moles of gas are constant):
P1V1=P2V2
Substituting the values we have:
65cmHg×(A×20cm)=85cmHg×(A×x)
Step 7: Simplify the Equation
Since A (the cross-sectional area) is common on both sides, we can cancel it out:
65×20=85×x
Step 8: Solve for x
Now, we can solve for x:
x=65×2085
Calculating this gives:
x=130085≈15.29cm
Conclusion
The length of the air column trapped when the tube is inverted is approximately 15.29 cm.
---
Initially, the tube is closed at one end and has a mercury pellet of length 10 cm. The air column trapped in the tube is 20 cm long. The atmospheric pressure is given as 75 cm of mercury (cmHg).
When the tube is upright (closed end up), the pressure exerted by the trapped air (P1) can be calculated using the atmospheric pressure and the height of the mercury column:
Where:
- Patm=75cmHg
- PHg=10cmHg (the height of the mercury column)
P1=75cmHg−10cmHg=65cmHg
The volume of the air column (V1) can be expressed in terms of the length of the air column (20 cm) and the cross-sectional area (A) of the tube:
When the tube is inverted (closed end down), the length of the air column is unknown (let's call it x). The pressure (P2) in this case is the atmospheric pressure plus the pressure due to the mercury column:
The volume of the air column (V2) when the tube is inverted can be expressed as:
According to the ideal gas law, the product of pressure and volume remains constant (assuming temperature and the number of moles of gas are constant):
Since A (the cross-sectional area) is common on both sides, we can cancel it out:
Now, we can solve for x:
The length of the air column trapped when the tube is inverted is approximately 15.29 cm.
Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - HC VERMACHAPTER - KINETIC THEORY OF GASESEXERCISE - Objective 2
7 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMACHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Exercises
19 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
Similar Questions
In given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)

View Solution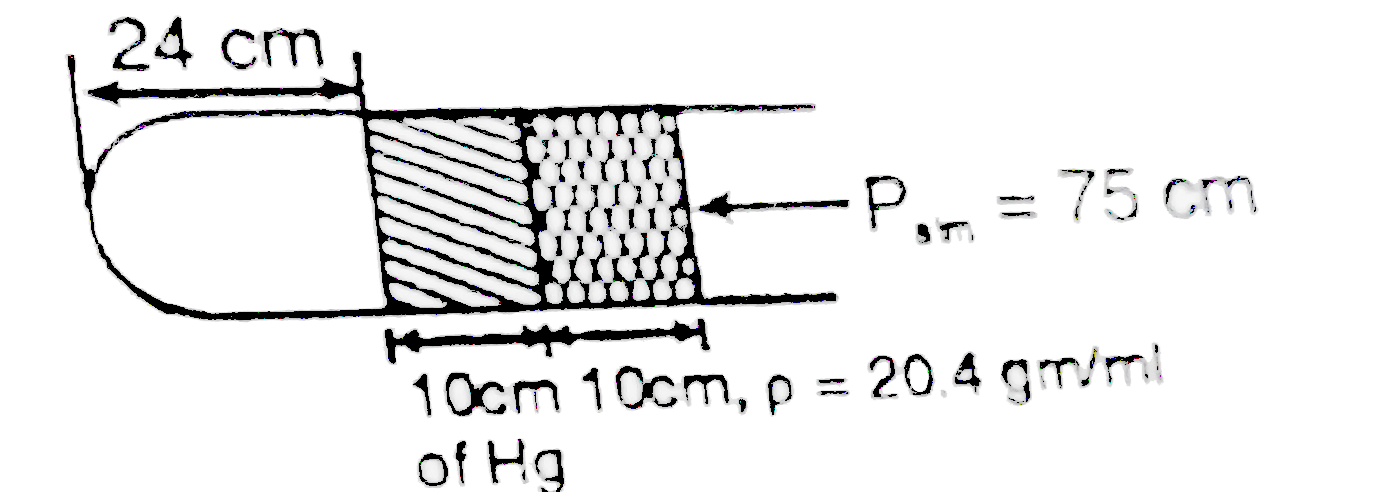
If above tube is placed vertically with the open and upward then find the length of the air column.
View Solution
Knowledge Check
A vertical tube of length 100 cm contains a mercury pallet of length 5 cm as shown in the figure. The length of the tube above mercury pallet if the tube is inverted is nearly: (atmospheric pressure = 75 cm Hg of Hg)
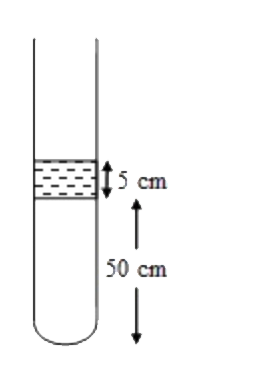 A56 cmB57 cmC60 cmD50 cm
A56 cmB57 cmC60 cmD50 cmA mercury tube of length
100 cm. open at one end is kept
vertically with open end upwards. It
is filled with 10 cm of mercury to
trap an air column of height
40 cm. what will be the length of
trapped air if it is held vertically
with open end downwards ?
[ Assume atmospheric pressure to be 1 atm]A40.00 cmB32.00 cmC52.12 cmD82.00 cm
A uniform tube closed at one end, contains a pallet of mercury 4 cm long. When the tube is kept vertically with closed end upwards, the length of air column between closed end and mercury pallet is 10 cm. the tube is inverted so that open end becomes upwards. find the length of trapped air column (in cm) trapped. take atmospheric pressure 76 cm of Hg.
View Solution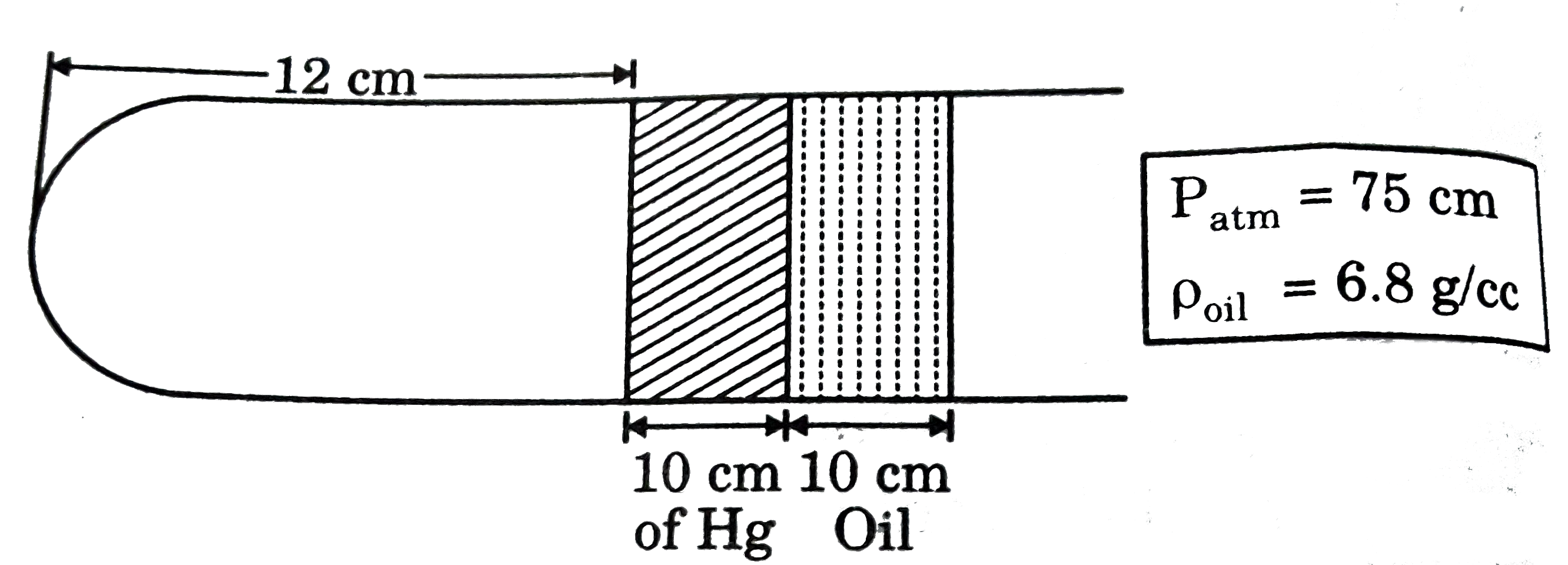
If above tube is held vertical with open end upward then find the length of air column (in cm).
View SolutionA Quill's tube of one metre is taken. A certain amount of ideal gas is trapped in it by a 20 cm length of Hg column. When the tube is held vertical with open end upwards, the length of the gas column is 50 cm. Find the pressure and length of the trapped gas, when the Quill's tube is kept in slanting position making 45∘ with the vertical open and upwards. (Take atmospheric pressure as 76 cm of Hg and √2=1.414).
View SolutionA narrow uniform glass tube contains air enclosed by 15 cm long thread of mercury. When the tube is vertical with open end uppermost, the air column is 30 cm long. When the tube is inverted, the length of air column becomes 45 cm. Calculate the atmospheric pressure.
View SolutionAn ideal gas in enclosed in a tube and is held in the vertical position with the closed end upward. The length of pellet of mercury entrapping the gas is h=10 cm and the length of the tube occupied by gas is l=40 cm. Calculate the length occupied by the gas when it is turned through θ=60∘ and 90∘. Atmospheric pressure , H=76 cm of mercury.
_E01_265_Q01.png)
View SolutionCalculate the length of mercury column in a barometer tube which is inclined at an angle of 45∘ with horizontal direction if the atmospheric pressure is 75 cm of mercury.
View Solution
