A uniform wooden bar of length l and mass m hinged on a vertical wall of a containing water, at one end.

3/5th part of the bar is submerged in water. Find the ratio of densities of the liquid and the bar.
Let ρ and simga be the density of the rod PQ and liquid respectively. If A is the area of cross - section of the rod, then the weight of the rod. W=Alρg. It acts downwards at the cente C of the rod. Upward thrust due to liquid on rod, FB=A×35lσg. It acts at the centre of the dipped part of the rof, i.e,. at B. Taking moment of forces about point P, we have W(l/2)sinθ−FB(l−3l/10)sinθ=0
or Alρg×l2sinθ=A×35lσg×7l10sinθ
or ρ2=35σ×710orσρ=2521

Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Value Based Question5videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Test Your Grip A10videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - NCERT Questions73videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
Similar Questions
A conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View SolutionA uniform bar of length I and mass m stands vertically touching a vertical wall (y-axis). When slightly displaced, its lower end begins to slide along the floor (x-axis). Obtain an expression for the angular velocity (ω) of the bar as a function of O. Neglect friction everywhere.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A bar of length l canying a small mass m at one of its ends rotates with a uniform angular speed ω in a vertical plane about the mid-point of the bar. During the rotation, at some instant of time when the bar is horizontal, the mass is detached from the bar but the bar continues to rotate with same ω. The mass moves ve1tically up, comes back and reaches the bar at the same point. At that place, the acceleration due to gravity is g.
Athis is possible if the quantity ω2l2πg is an integerBthe total time of flight of the mass is proportional to ω2Cthe total distance travelled by the mass in air is proportional to ω2Dthe total distance travelled by the mass in air and its total time of flight are both independent of its mass.
A uniform bar AB of length 6a has been placed on a horizontal smooth table of width 5 a as shown in the figure. Length 2a of the bar is overhanging. Mass of the bar is 4m. An insect of mass m is sitting at the end A of the bar. The insect walks along the length of the bar to reach its other end B.
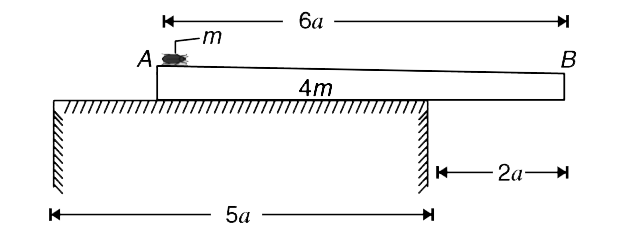
(a) Will the bar topple when the insect reaches end B of the bar ?
(b) After the insect reaches at B, another insect of mass M lands on the end A of the bar. Find the largest value of M which will not topple the bar.View SolutionA thin uniform bar of length L and mass 8m lies on a smooth horizontal table .Two point masses m and 2 m are moving in the same horizontal plane from opposite sides of the bar with speeds 2v and v respectively .The masses stick to the bar after collision at a distances L3andL6 respectively from the center of the bar if the bar starts rotating about its center of mass as result of collision the angular speed of the bar will be
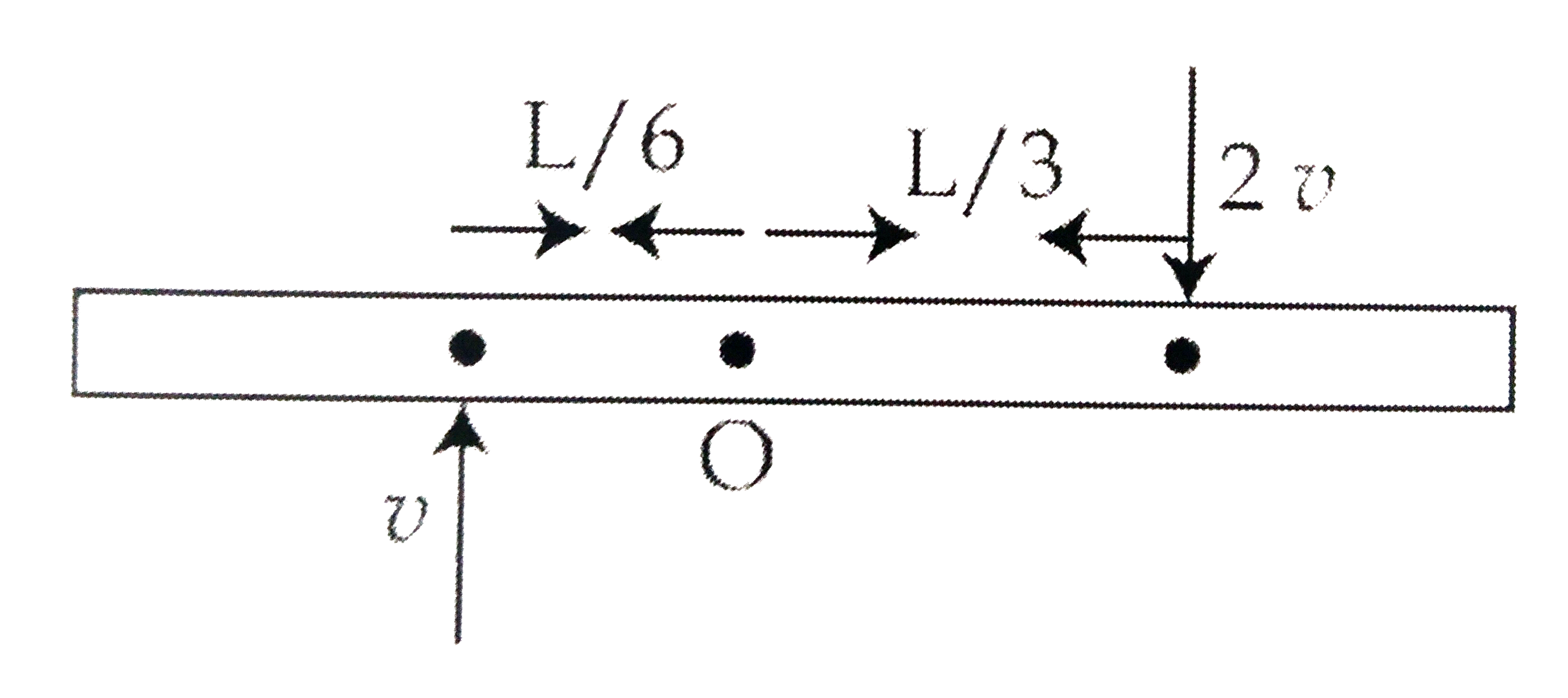 View Solution
View SolutionA.uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speed 2v and v, respectively, strike the bar and stick to the bar. The bar is set in rotation. The rotational energy E=pmv2q then find (p+q).
'(##CEN_KSR_PHY_JEE_C09_E01_038_Q20##)'View SolutionOne end of a board of length l is hinged on top of a stone protruding from water . Length a of the board is above the point of support (Fig) . What part of the board is below the surface of the water in equilibrium state , if the density of wood is γ ?
View SolutionA thin uniform rod of length 2l and specific gravity 3/4 is hinged at one end to height l/2 above the surface of water, with the other end immersed. Find the inclination of rod in equilibrium
View SolutionThere are two cylinder shaped wooden billets, each having mass M, in a vertical wall sewage, which contains water in it. The two billets have same size and same material , they touch each other and walls of sewage. One of them is totally under water, whilst the other one is immersed only half into water. Friction is negligible if density of wood is given by 3xpω(pωis density of water)then find x
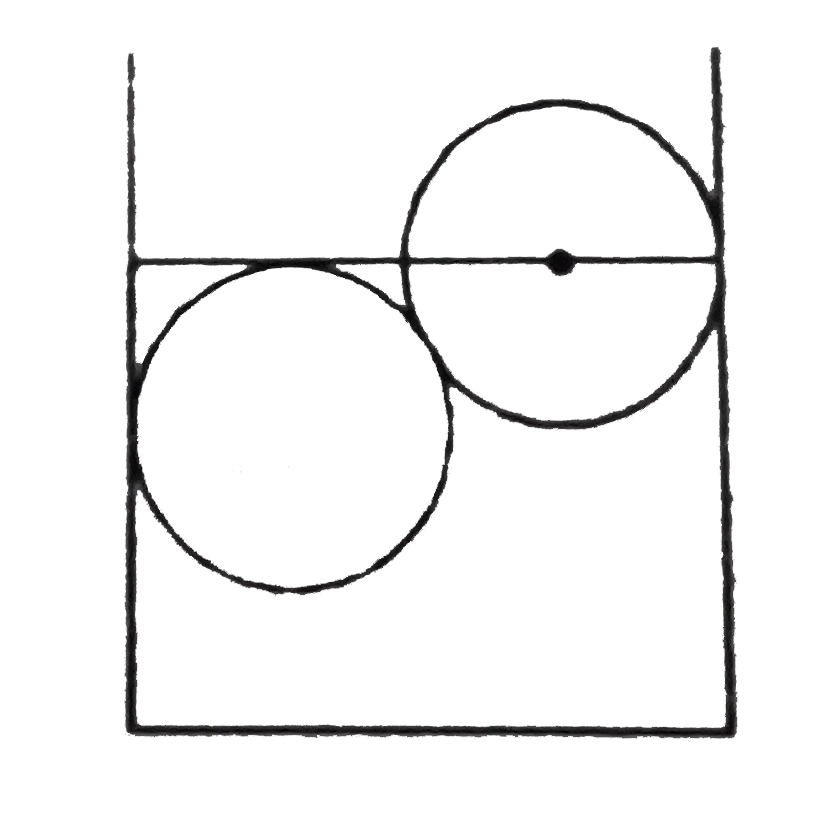 View Solution
View Solutionthere is a bar of length a cm whose one end is on origin and other end is on the X-axis find Co ordinate of both the ends of the bar
View Solution

