(a) Use the Bio-Savart law to determine the magnetic field due to conduction current outside the plates (refer to Fig) at points 6.5cm,12cm and 15cm from the wire. Do the answer match with those in Ex. ? Explain.
(b) If the conduction wire has a radius of 1.0mm, what is the maximum value of magnetic field due to the conduction current? [When you compare the answer to Ex.(b) and 6(b), you will appreciate why it is not easy to notice magnetic field due to the displacement current].
(c) Suppose the thin wire in Fig. is replaced by rods each of radius 12cm (i.e. we now have two long cylinder rods separated by a small gap). Will magnetic field configurations for r>R be identical for the regions between the plates and outside the plates?
(a) Using Biot-Savart law, mangetic
field induction at a point outside a straight current
carrying wire is given by
B=μ0ID2πr
Now, since I=ID, this formula is the same as
in for r>R. Therefore , for r=12cm and
15cm, answers are the same as in For
r=6.5cm(r<R), the two formulae differ. Here
B=4.6×10−7T, greater than B is
(b) B is maximum at the surface of the wire,
B=μ0I2πr=4π×10−72π×10−3=3.0×10−6T
[Here, r=1.0mm=10−3m]
This is much greater than the maximum value
of B in Due to this reason, it is not easy to
notice magnetic field due to displacement current.
(c) Yes, sinceI=ID, magnetic field
Configuration are identical for r>R.
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - (I) Conceptual problems
1 Videos
- ELECTROMAGNETIC WAVESBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Conceptual problems
3 Videos
- ELECTROMAGNETIC WAVESBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question
5 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Multiple Choice Questions
1 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
Similar Questions
Knowledge Check
Due to currents in infinite long wire at A and B, magnetic field is maximum at M and at P, magnetic field as shown. Then
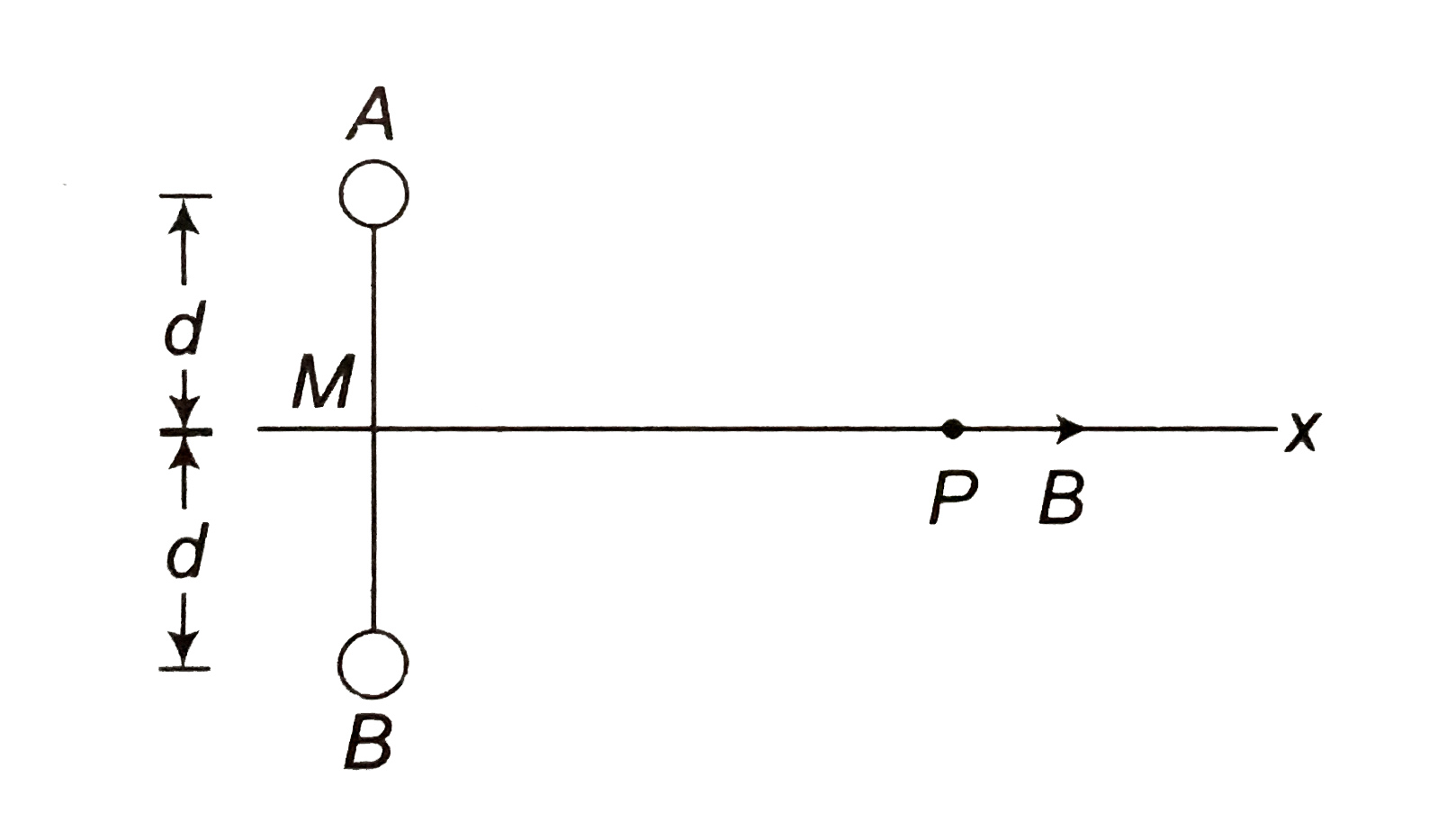 ACurrent is A and B is equal in magnitude and outside the plane of paperBCurrent is A and B is equal in magnitude and inside the plane of paperCCurrent in A and B is equal in magnitude, in A outside, in B insideDCurrent in A and B is equal in magnitude, in A inside, in B inside
ACurrent is A and B is equal in magnitude and outside the plane of paperBCurrent is A and B is equal in magnitude and inside the plane of paperCCurrent in A and B is equal in magnitude, in A outside, in B insideDCurrent in A and B is equal in magnitude, in A inside, in B inside
A copper wire of diameter 1.6 mm carries a current of 20A. Find the maximum magnitude of the magnetic field (vec B)due to this current.
View SolutionA copper wire of diameter 1.6 mm carries a current of 20A. Find the maximum magnitude of the magnetic field (vec B)due to this current.
View SolutionA copper wire of diameter 1.6 mm carries a current of 20A. Find the maximum magnitude of the magnetic field (→B) due to this current.
View SolutionState Biot- Savart law. Use to obtain the magnetic field at a point due to a long, staright current carrying wire.
View SolutionMagnetic Field Due To A Current Carrying Straight Conducting Wire
View SolutionA long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
View Solution(a) State Bio-Savart's law in vector form expressing the magnetic field due to an element →dl carrying current I at a distance r from the element.
(b) Write the expression for the magnitude of the magnetic field at the centre of a circular loop of radius 'R' carrying a steady current I. Draw the field lines due to the current loop.
View Solution
