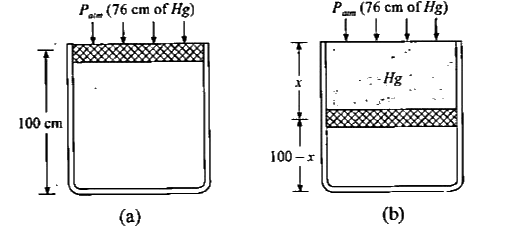
A vertical cylinder of height 100cm contains air at a constant temperature. The top is closed by a friction less light piston. The atmospheric pressure is equal to 75 cm of mercury. Mercury is slowly poured over the piston. Find the maximum height of the mercury column that can be put on the piston.
Given, P1=A→mosphericpressure
=75×ρg,
V1=100×A
(P2)=Atmosphericpressure
+ Mercury pressure
=75ρg+hρg
(ifh=heightofmercury)
V2=(100−h)
((P1)(V1))=((P2)(V2))
⇒75ρg(100A)
=((75+h)ρg(100−h)A)
⇒(75×100)=((75+h)(100−h))
⇒7500=7500−75h+100h−(h2)
⇒(h2)−100h+75h=0
h2−25h=0
⇒(h2)=25h
h=25cm
Height of Mercury that can be poured
=25cm .
Topper's Solved these Questions
Similar Questions
A vertical cylinder of height 100 cm contains air at a constant temperature and its top is closed by a frictionless piston at atmospheric pressure (76 cm of Hg) asshown in figure-2.12. If mercury is slowly poured on the piston, due to its weight airis compressed. Find the maximum height of the mercury column which can be put on the piston.
View SolutionAn ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View Solution
Knowledge Check
Atmospheric pressure is 76 cm Hg and pressure of the gas is 77 cm Hg. Hence, height, 'h' of the mercury column in open arm is
A1 cmB113.6×980cmC153 cmD1×1.36×980 cmA vertical tube of length 100 cm contains a mercury pallet of length 5 cm as shown in the figure. The length of the tube above mercury pallet if the tube is inverted is nearly: (atmospheric pressure = 75 cm Hg of Hg)
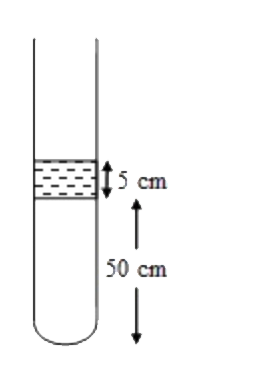A56 cmB57 cmC60 cmD50 cmAs shown , a piston chamber pf cross section area A is filled with ideal gas. A sealed piston of mass m is right at the middle height of the cylinder at equilibrium. The friction force between the chamber wall and the piston can be ignored . The mass of the rest of the chamber is M.The atmosphere pressure is P0. Now slowly pull the piston upwards , find the maximum value of M such that the chamber can be lifted off the ground. The temperature remains unchanged.
_E01_049_Q01.png)
AM=P0A−2mg2gBM=P0A−mg2gCM=P0A−mggDM=P0A2g
A vertical tube of length 100 cm contains a mercury pallet of length 5 cm as shown in the figure. The length of the tube above mercury pallet if the tube is inverted is nearly: (atmospheric pressure = 75 cm Hg of Hg)
View SolutionAs shown , a piston chamber pf cross section area A is filled with ideal gas. A sealed piston of mass m is right at the middle height of the cylinder at equilibrium. The friction force between the chamber wall and the piston can be ignored . The mass of the rest of the chamber is M.The atmosphere pressure is P0. Now slowly pull the piston upwards , find the maximum value of M such that the chamber can be lifted off the ground. The temperature remains unchanged.
View SolutionA horizontal tube of 1m is closed at both ends. A mercury column of 20 cm is contained in the middle of the tube and two equal lengths of this tube contain air at an atmospheric pressure of 76cm. The tube is now placed vertically. Calculate the distance through which the mercury column will be displaced at a constant temperature.
View SolutionA column of mercury is in the middle of horizontal tube of uniform cross section closed at both ends. The pressure of the enclosed air column on either side of the mercury is 75 cm of mercury column. When the tuve is placed vertical the length air below the mercury column is 35 th of that above it. if length of mercury column is 10n cm. find n.
View SolutionA column of mercury is in the middle of horizontal tube of uniform cross section closed at both ends. The pressure of the enclosed air column on either side of the mercury is 75 cm of mercury column. When the tuve is placed vertical the length air below the mercury column is 35 th of that above it. if length of mercury column is 10n cm. find n.
View Solution