A very thin round plate of radius R carrying a uniform surface charge density σ is located in vacumm. Find the electric field potentail and strength along the plate's axis as a function of a distance l from its centre. Investigation the obtained expression of l→0 and l>>R.
Let us consider an elementary ring of of thickness dy and rasdius y as shown in fig. Then potential at a point p at distance l from the centre of the disc, is
dφ=σ2πydy4πε0(y2+l2)1/2
Hence potential due to the whole disc,
φ=∫R0σ2πydy4πε0(y2+l2)1/2=σl2ε0(√1+(R/l)2−1)
From symmtry
E=E1=dφdl
=−σ2ε0[2l2√R2+l2−1]=σ2ε0⎡⎢
⎢⎣1−1√1+(R/l)2⎤⎥
⎥⎦
when l→0,φ=σR2ε0,E=σ2ε0 and when l>>R,
φ=σR24ε0l,E=σR24ε0l2

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field
47 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Find the electric field potentail and strength at the centre of a hemisphere fo raidus R ahcged uniformly with the the surface density σ.
View SolutionA uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View Solution
Knowledge Check
The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
A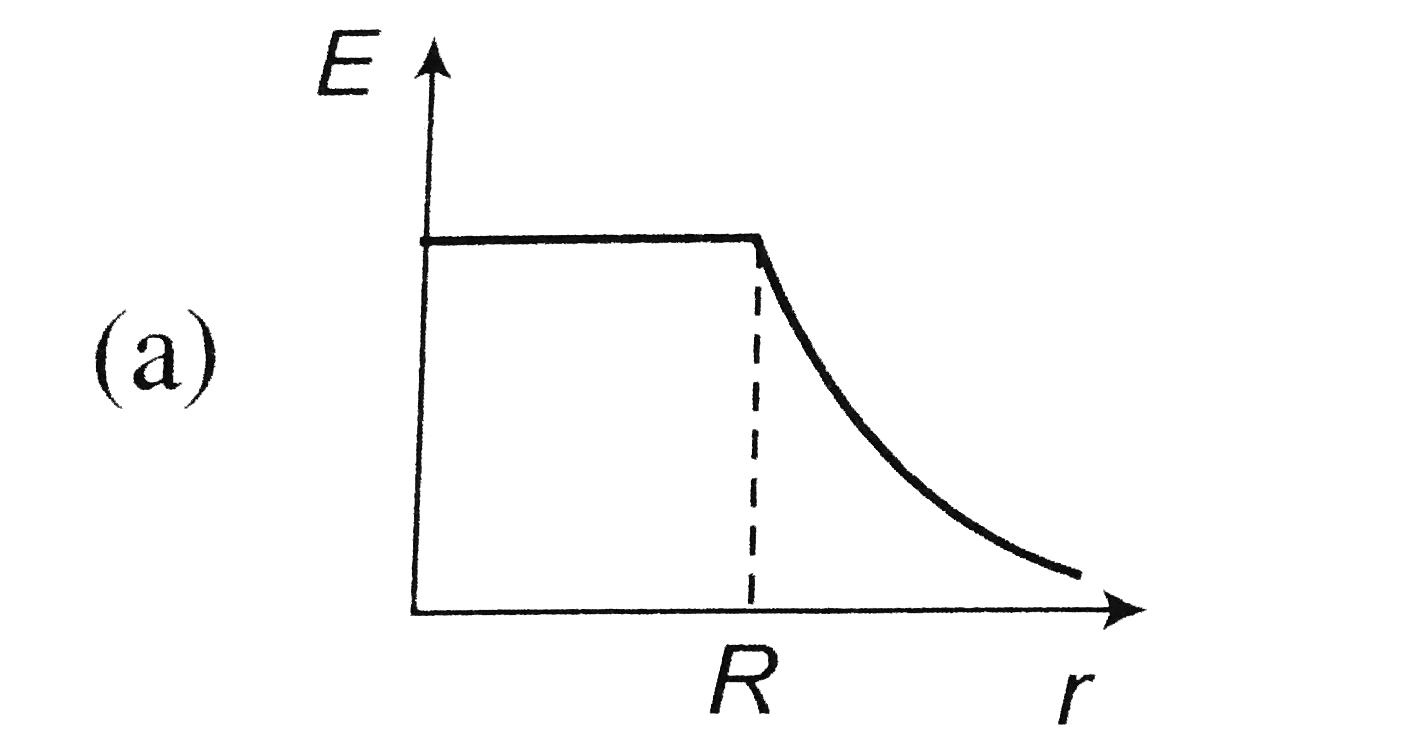 B
B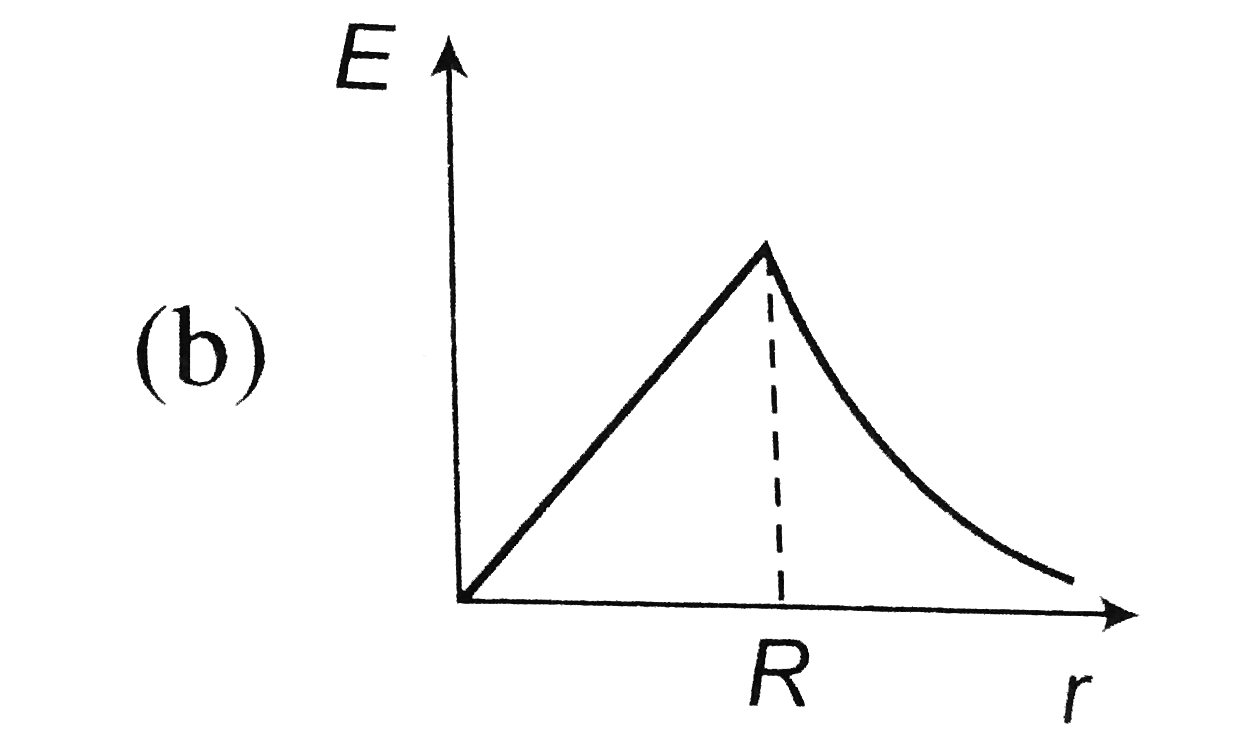 C
C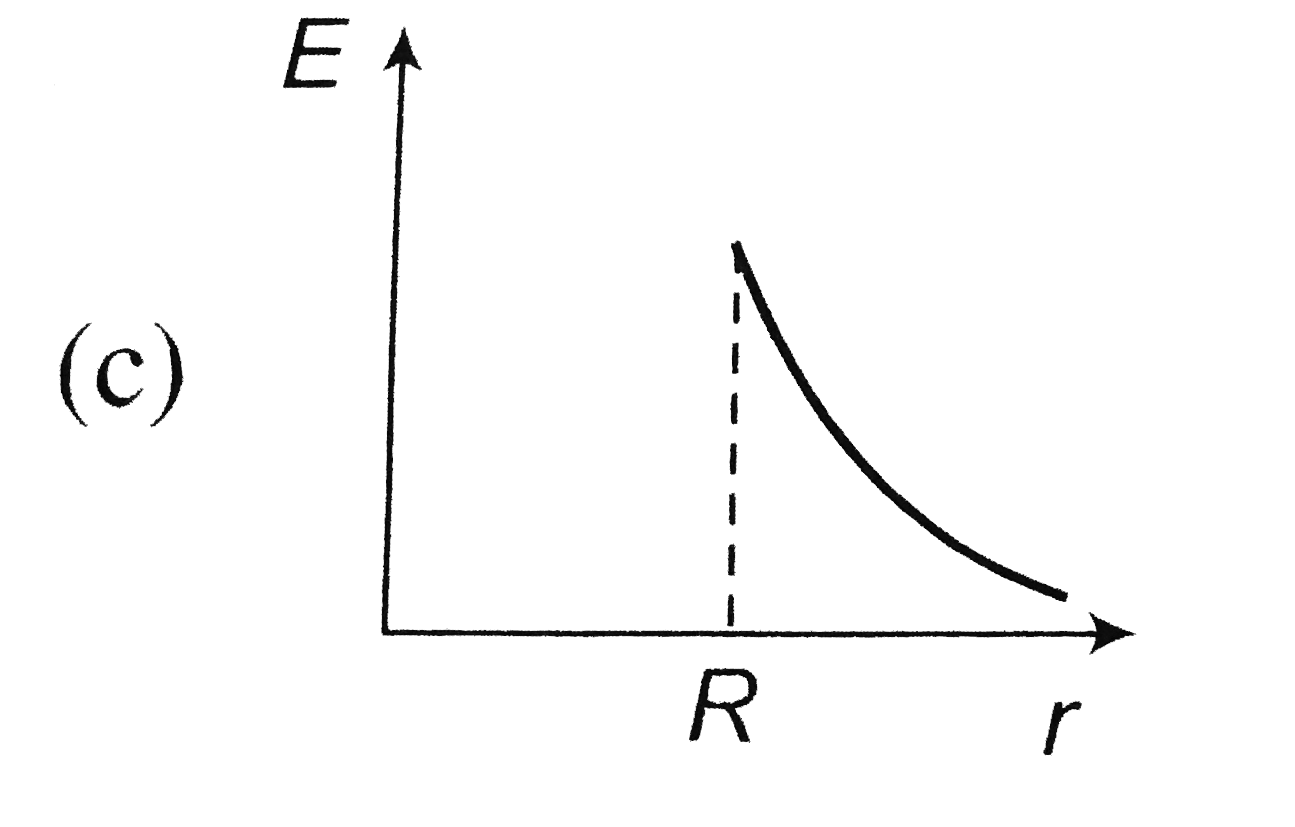 D
D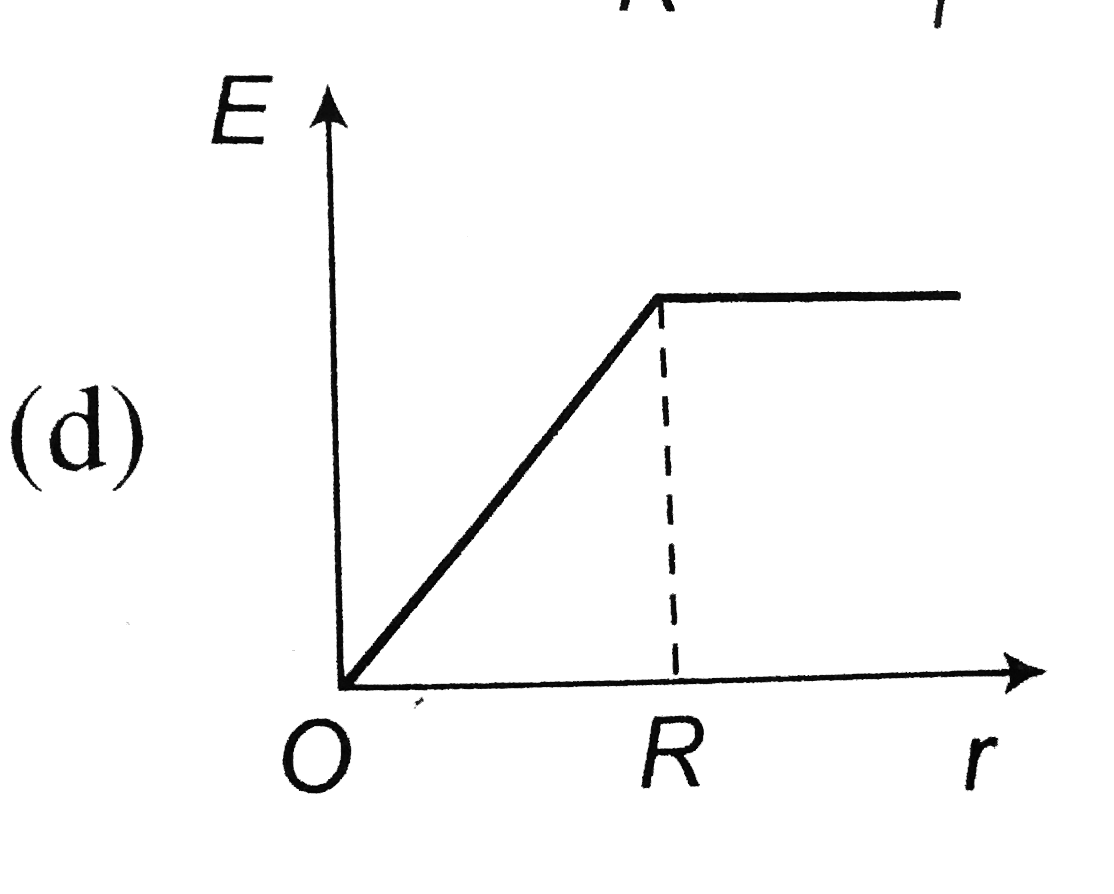
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2Graphical representation of electric field due to uniformly charged sphere of radius R as function of distance from its centre is given by:
A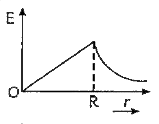 B
B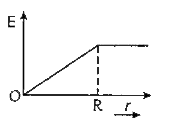 C
C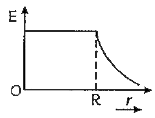 D
D
A uniform disc of radius R is charged with a uniform surface charge density σ. Find the electric potential due to the charges on the disc at a point on its edge. [σRπ∈0]
View SolutionAn electric capacitor consists of this round parallel plates. each of radius R, separated by a distance l(l<<R) and uniformly charged with surface densities σ and −σ . Find the potential of the electirc field and the magnitude of tis strength vector at the axes of the capacitor as functions of a distanace x from the plates if x>>l. Investigate and obtained expressions at x>>R.
View SolutionA thin straight rod of length 2a carrying a uniformly distributed charge q is located in vacumm. Find the magnitude of the electric field strength as a function of the distatance r from the rod's centre along the streaight line
(a) perpendicular to the rod and passing through its centre ,
(b) coinciding with the rod's direction (at the point lying outside the rod).
View SolutionA thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimutahl angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
View SolutionTwo coaxial rings, eacg of radius R, made of thin wire are separated by a small distabce l(l<<R) and carry the charges q and −q. Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x|>>R
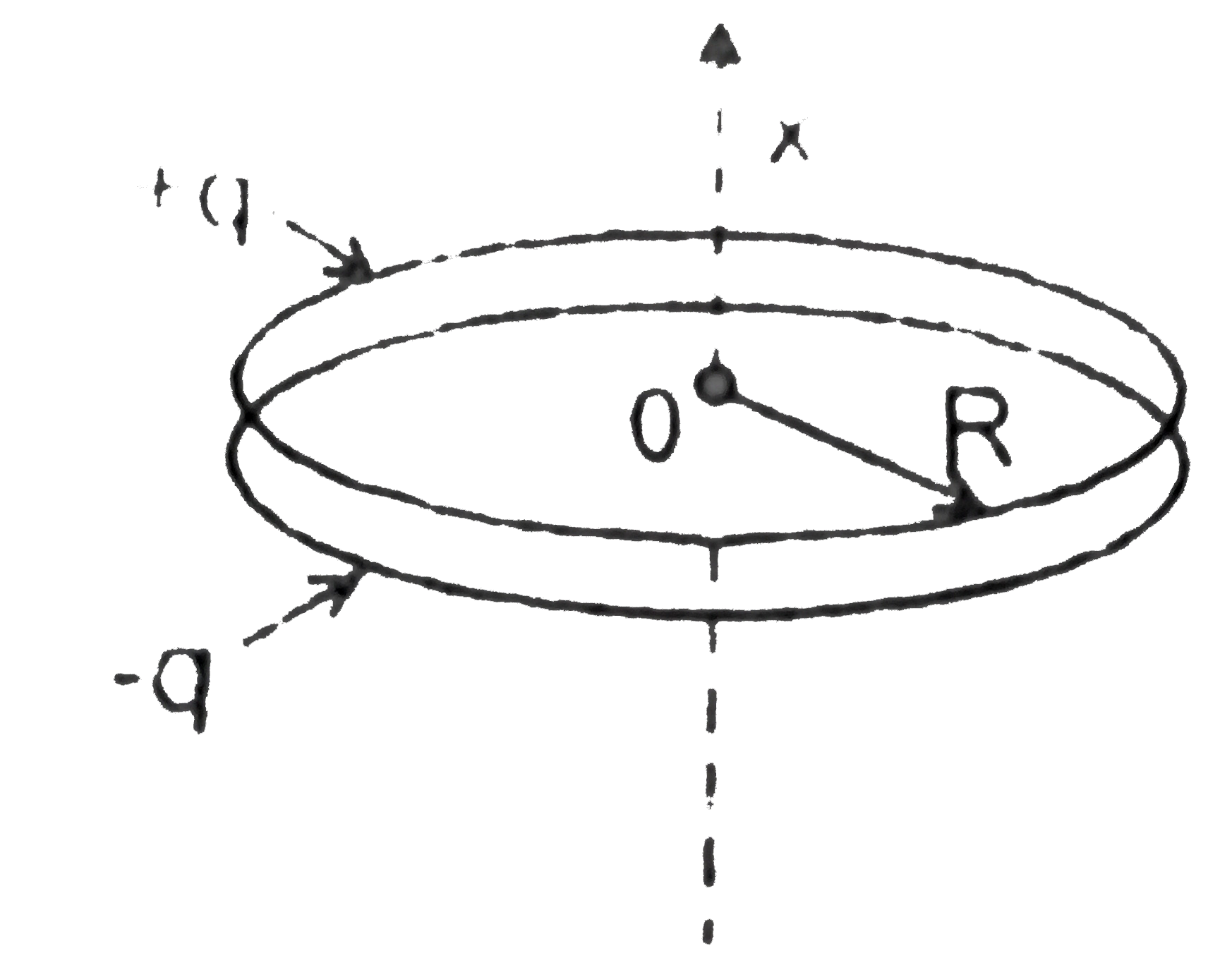
View Solution
