Two persons are pulling a heavy block with the help of horizontal inextensible strings. At the instant shown, the velocities of the two persons are v1 and v2 directed along the respective strings with the strings making an angle of 60∘ between them.
(a) Find the speed of the block at the instant shown.
(b) For what ratio of v1 and v2 the instantaneous velocity of the block will be along the direction of v1.

The correct Answer is:(a) 2√3√v21+v22−v1v2 (b) v1v2=2
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the arrangement shown, end A of light intextensible string is pulled with constant velocity v. the velocity of block B is
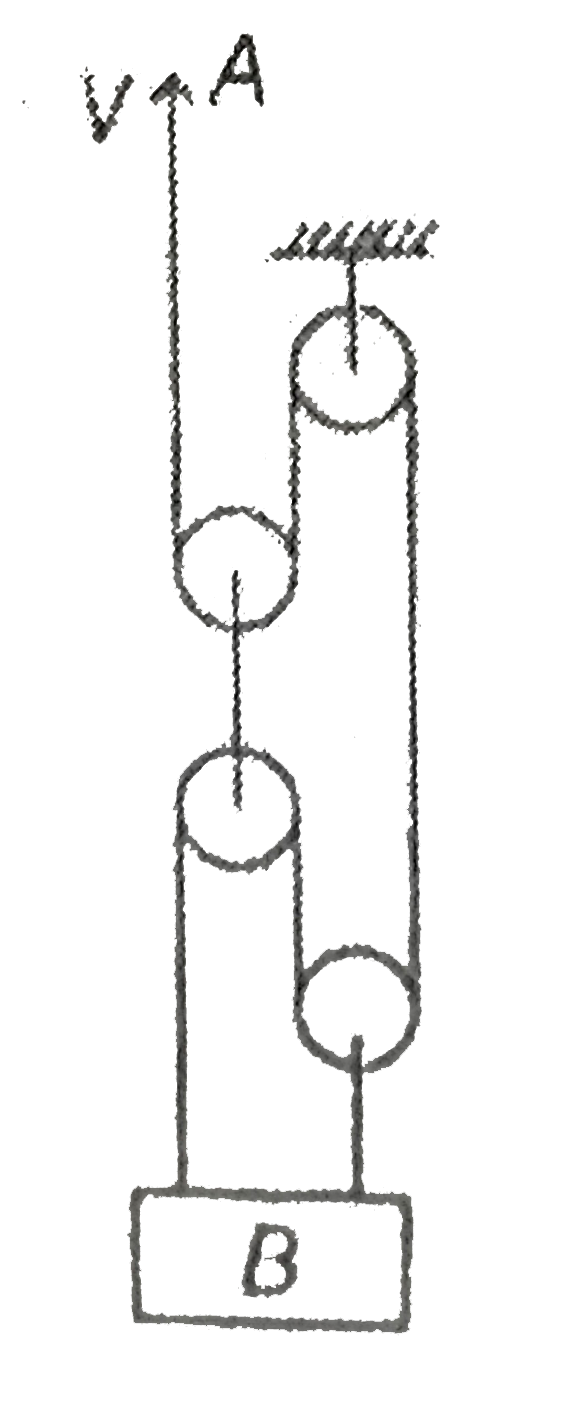 AV/2BvCv/3D3v
AV/2BvCv/3D3vIf block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
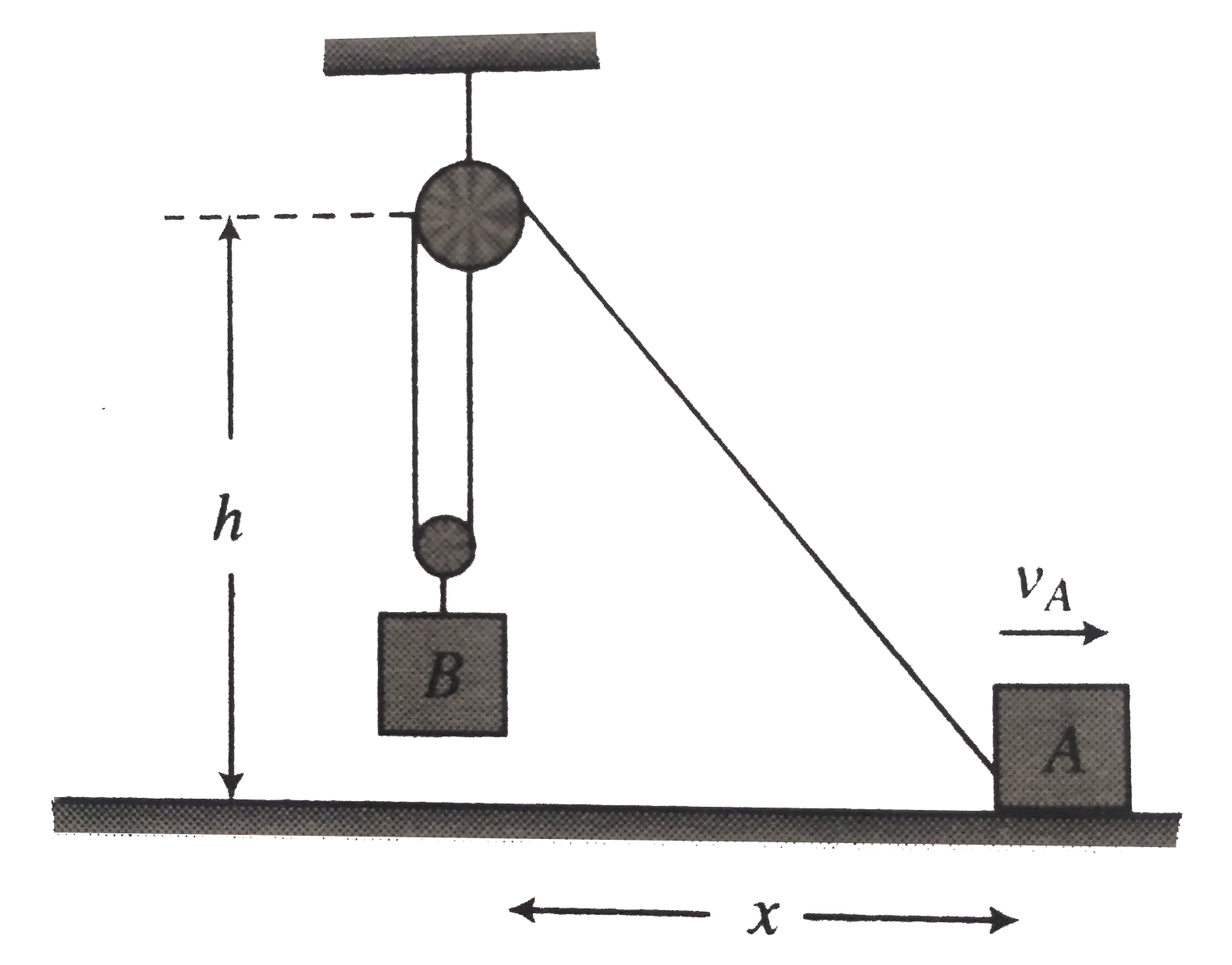 AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2
AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2In the arrangement shown, blocks A and B connected with an inextensible string move with velocities v1 and v2 along horizontal direction. The ratio of v2v1 is:
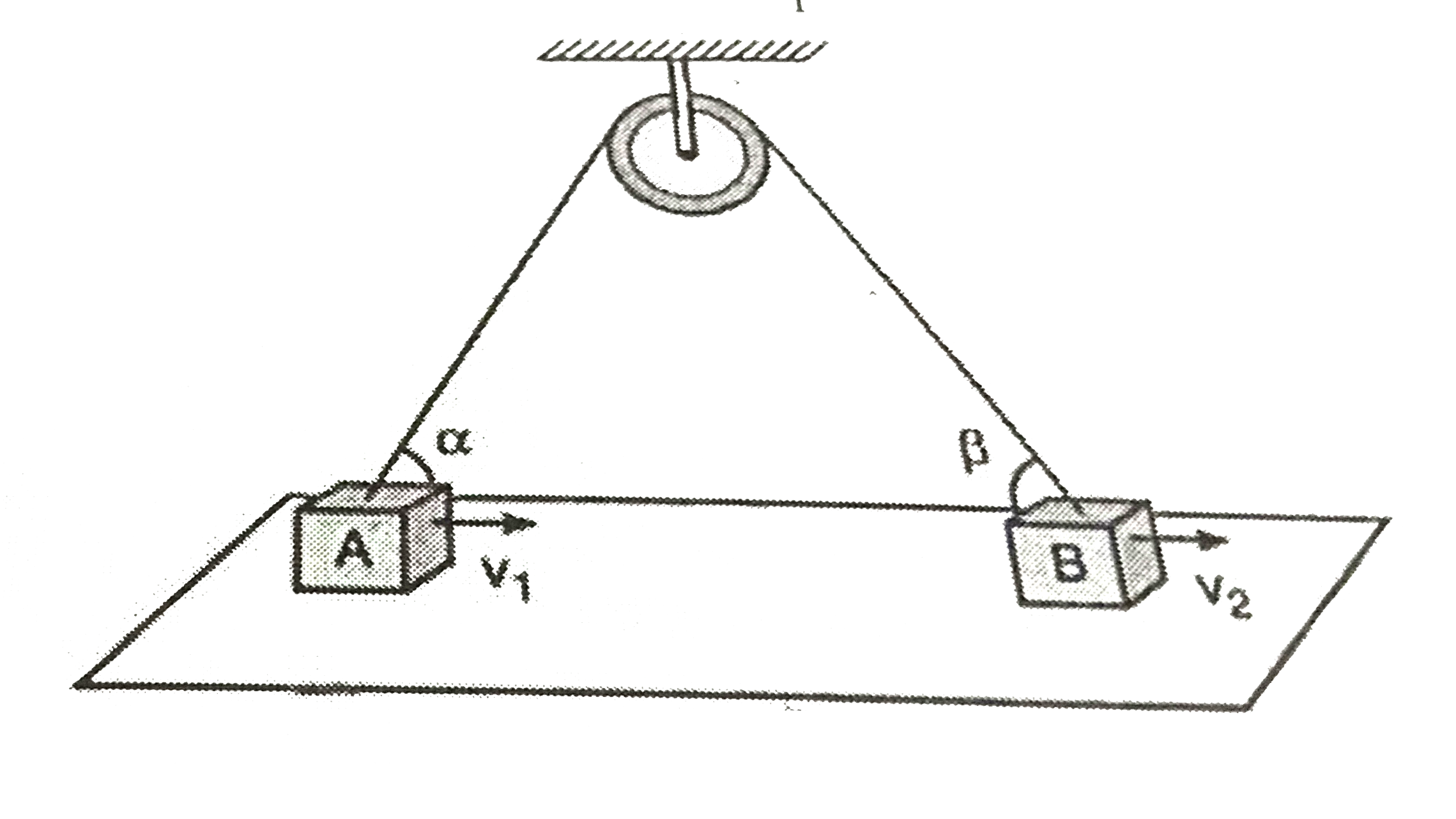 AsinαsinβBsinβsinαCcosβcosαDcosαcosβ
AsinαsinβBsinβsinαCcosβcosαDcosαcosβ
The block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View SolutionIn fig. a ball of mass m1 and a block of mass m2 are joined together with an inextensible string. The ball can slide on a smooth horizontal surface. If v1 and v2 are the respective speeds of the ball and the block, then determine the constraint relation between the two.
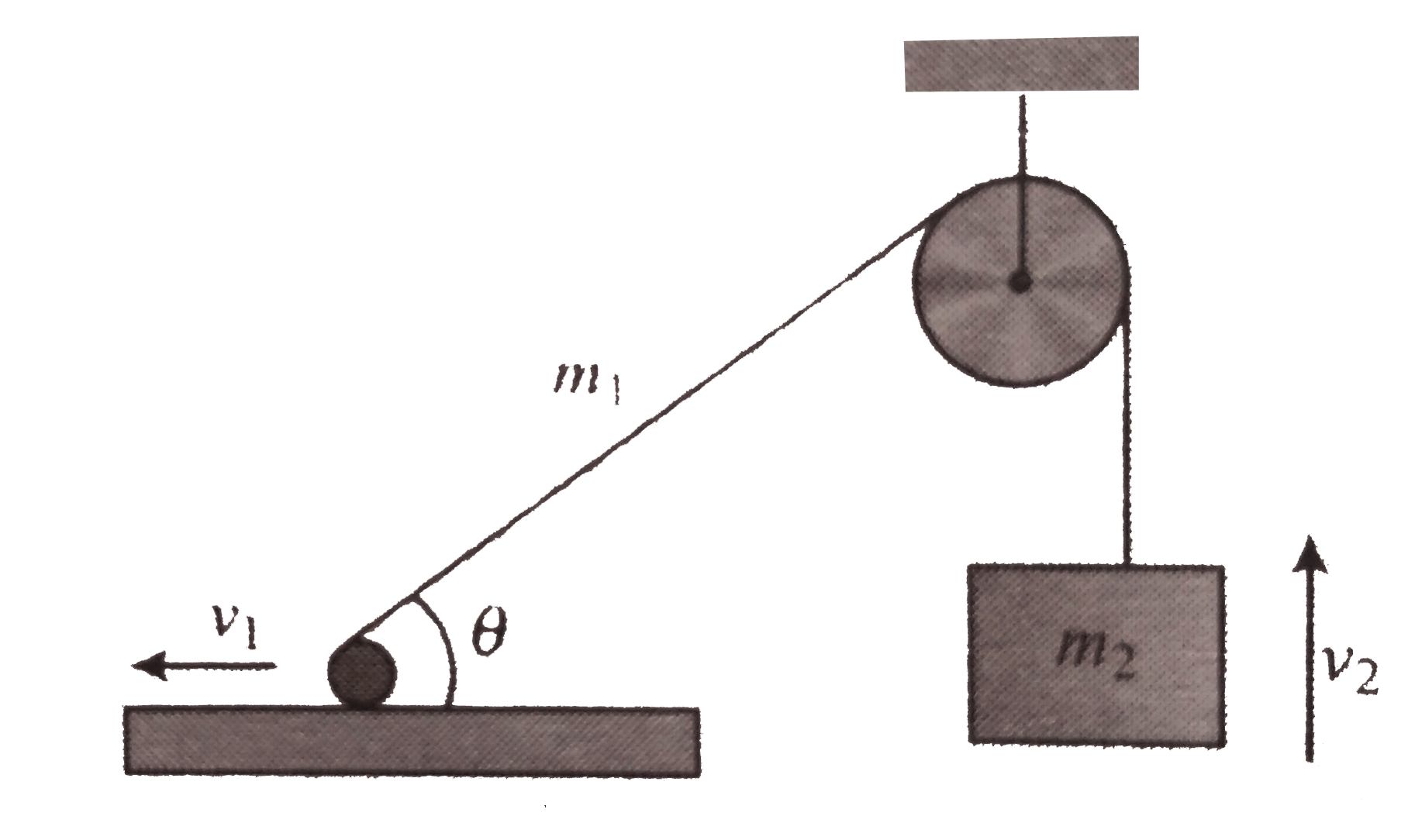
View SolutionIn fig. a ball of mass m1 and a block of mass m2 are joined together with an inextensible string. The ball can slide on a smooth horizontal surface. If v1 and v2 are the respective speeds of the ball and the block, then determine the constraint relation between the two.

View SolutionTwo blocks are attached by a light inextensible string and the system is pulled by applying a force F0 as shown in the diagram. Find the acceleration of each block and tension in the string.

View Solution
