A wave pulse on a horizontal string is represented by the function
$y (x, t) = \frac{5.0}{1.0 + {(x - 2 t)}^{2}}$ (CGS units)
plot this function at $t = 0, 2.5$ and $5.0 s$ .

Video Solution

Text Solution

Verified by Experts

At the given times the function repressenting the wave pulse is
$y (x, 0) = \frac{5.0}{1.0 + x^{2}}$
$y (x, 2.5 s) = \frac{5.0}{1.0 + {(x - 5.0)}^{- 2}}$
$y (x, 5.0 s) = \frac{5.0}{1.0 + {(x - 10.0)}^{2}}$

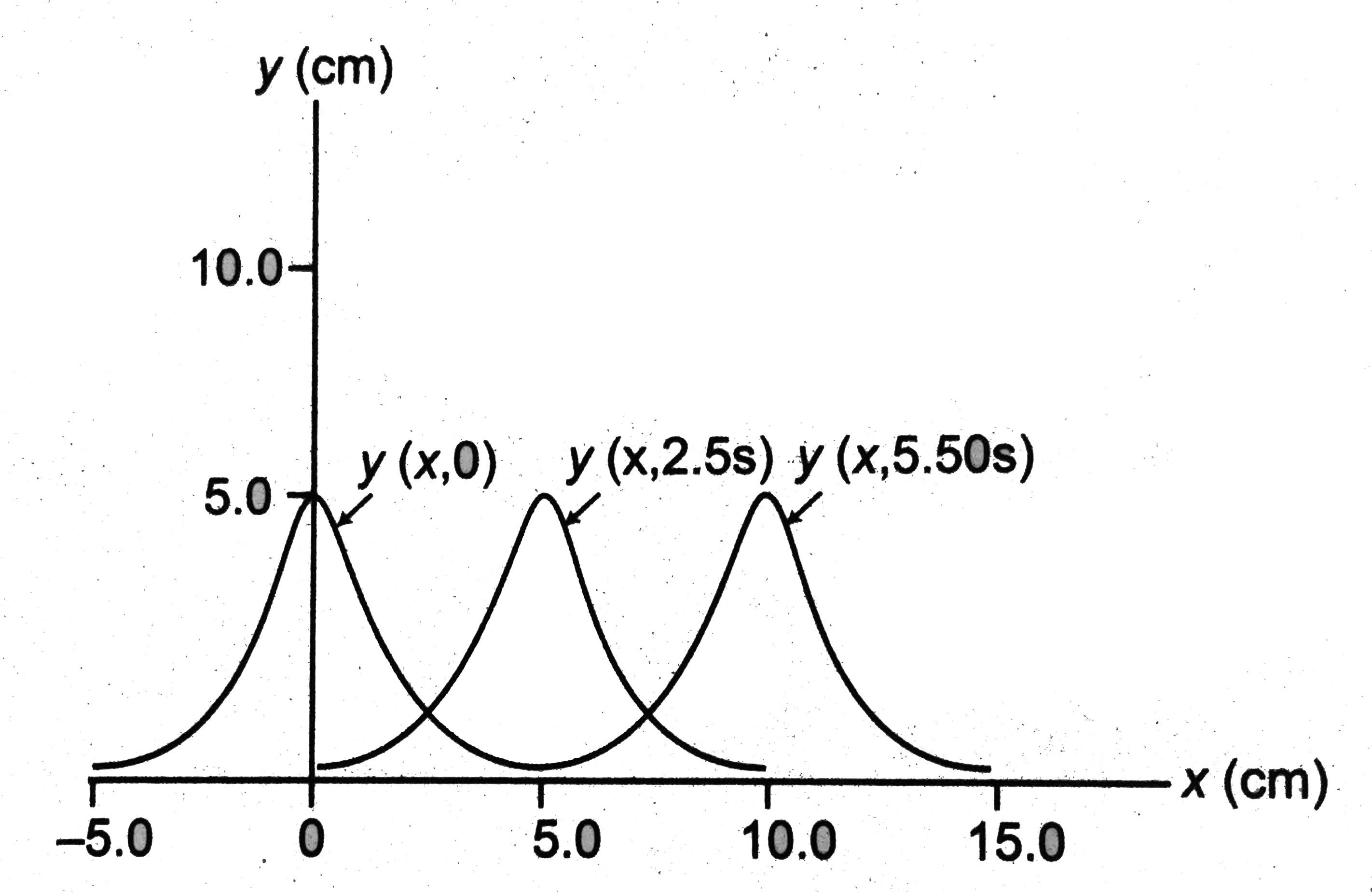
The maximum of $y (x, 0) i s$ 5.0 cm $, a t$ t = 0 $, i t i s l o c a t e d a t$ x = 0 $. A t$ t =2.5 $and$ 5.0 s $, t h e max i μ m o f t h e p s - e h a s m o v e d \to$ x= 5.0 $and$ 10.0 cm $, r e s p e c t i v e l y . S o, \in e a c h$ 2.5 s $t i m e \int e r v e l, t h e p s - e m o v e s$ 5.0 cm $\in t h e p o s i t i v e x - d i r e c t i o n . I t s v e l o c i t y i s ∴$ +2.0 cm//s.

Updated on:21/07/2023

A wave is represented by the equation $y = (0.001 m m) sin [(50 s^{- 10} t + (2.0 m^{- 1}) x]$
AThe wave velocity $= 100 m s^{- 1}$
BThe wavelength =2.0m
Cthe frequencey $= \frac{25}{π} H z$
DThe amplitude =0.001mm
The amplitude of a wave represented by the equation $y = 3 sin (5 x - 0.5 t) + 4 cos (5 x - 0.5 t)$ , is
A7
B4
C3
D5
If at $t = 0$ , a travelling wave pulse on a string is described by the function.
$y = \frac{6}{x^{2} + 3}$
What will be the waves function representing the pulse at time $t$ , if the pulse is propagating along positive x-axis with speed $4 m / s$ ?
A $y = \frac{6}{{(x + 4 t)}^{2}} + 3$
B $y = \frac{6}{{(x - 4 t)}^{2}} + 3$
C $y = \frac{6}{{(x - t)}^{2}}$
D $y = \frac{6}{{(x - t)}^{2}} + 12$