
A weightless rigid rod with a small iron bob at the end is hinged at point A to the wall so that it can rotate in all directions. The rod is kept in the horizontal position by a vertical inextensible string of length 20cm, fixed at its midpoint. The bob is displaced slightly perpenducular to the plane of the rod and string. Find period of small oscillations of the system in the form πX10s and fill the value of X.
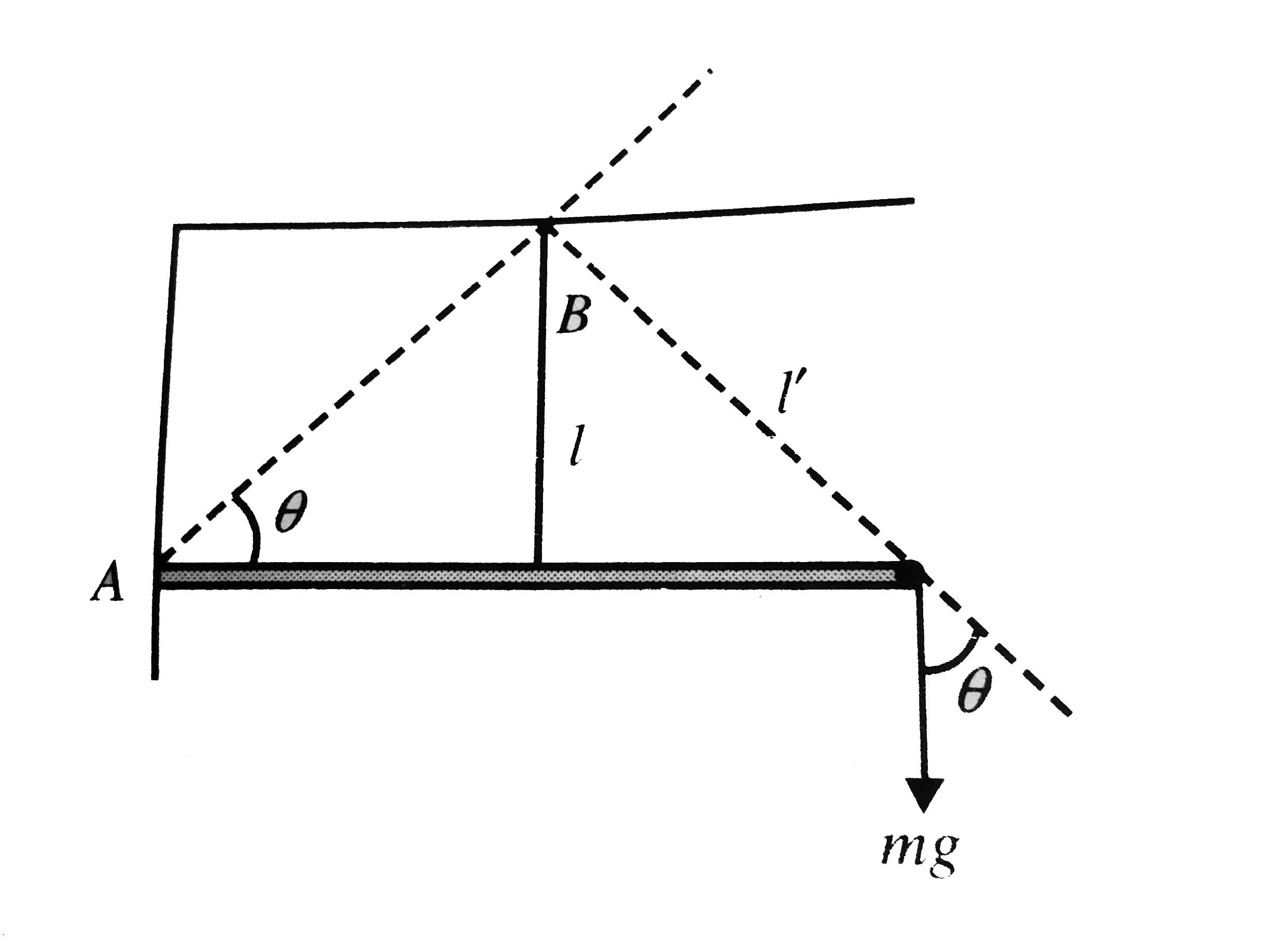
The bob will exicute SHM about the stationary axis passing through AB. If its effective length is l then T=2π√l'g'
l'=lsinθ=√2l
[because θ=45∘]
g)=gcostheta=(g)/(sqrt2_)<br>T=2pisqrt((2l)/(g))=2pisqrt((2xx0.2)/(10))=(2pi)/(5)s<br>X=4
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct Answer Type
29 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension
33 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).
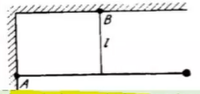
The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View SolutionThere is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionFind the period of small oscillations of a uniform rod with length l , pivoted at one end.
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
The acceleration of end B of the rod is
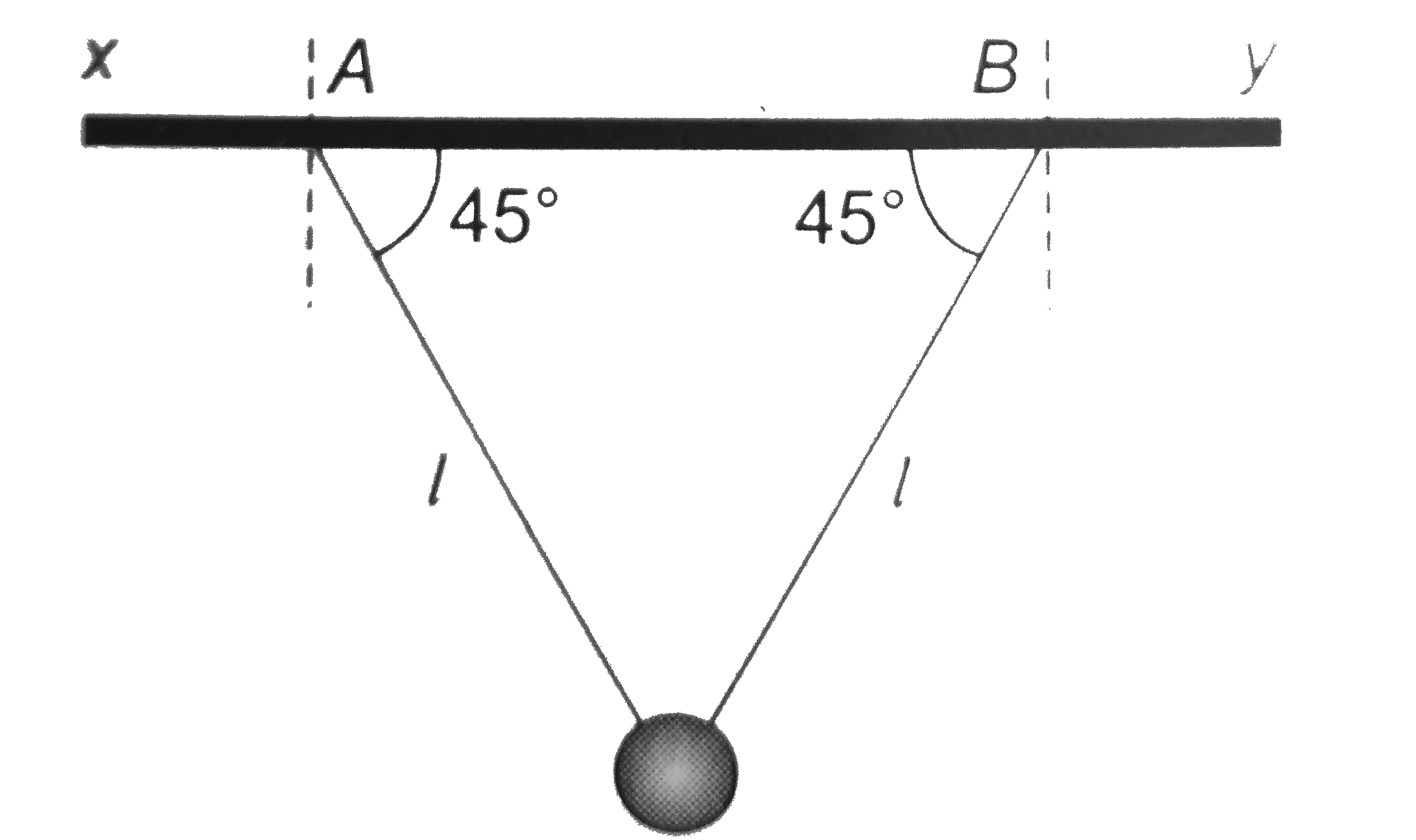
View SolutionTwo light strings, each of length l are fixed at points A andB on a fixed horizontal and xy A small are making angle 45∘ with the bob if the bob is displaced normal to the plane of the string and released then period of the resulting small oscillation will be
View SolutionA uniform rod of mass m and length L is hinged at one of its end with the ceiling and another end of the rod is attached with a thread which is attached with the horizontal ceiling at point P. If one end of the rod is slightly displaced horizontally and perpendicular to the rod and released. If the time period of small oscillation is 2π√2lsinθxg . Find x.

View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:

The acceleration of the centre of mass of the rod is
View SolutionA bob of mass m suspended by a light inextensible string of length 'l' from a fixed point. The bob is given a speed of √6gl. Find the tension in the string when string deflects through an angle 120∘ from the vertical.
View Solution
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View Solution
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View Solution