A wheel of radius R is rolling without sliding uniformly on a horizontal surface. Find the radius of curvature of the path of a point on its circumference when it is at highest point in its path.
The correct Answer is:4R
To find the radius of curvature of the path of a point on the circumference of a wheel when it is at the highest point in its path, we can follow these steps:
Step 1: Understand the Motion of the Wheel
The wheel is rolling without sliding on a horizontal surface. This means that at the point of contact with the ground, the velocity is zero, and the wheel rotates about its center of mass.
Hint: Remember that rolling without slipping means the point of contact does not slide over the surface.
Step 2: Identify the Velocity at the Highest Point
At the highest point of the wheel, the point on the circumference has a velocity that is the sum of the translational velocity of the center of mass (V) and the tangential velocity due to rotation (rω). Since the wheel rolls uniformly, we have the relation V=rω.
Hint: The total velocity at the highest point is the sum of the translational and rotational components.
Step 3: Calculate the Total Velocity
At the highest point, the total velocity Vtotal can be expressed as:
Vtotal=V+rω=V+V=2V
Hint: Substitute V with rω to find the total velocity at the highest point.
Step 4: Define the Radius of Curvature
The radius of curvature (ρ) is defined in terms of the centripetal acceleration. The centripetal acceleration ac for an object moving in a circular path is given by:
ac=V2totalρ
Hint: Remember that centripetal acceleration is necessary for circular motion.
Step 5: Set Up the Equation for Centripetal Force
At the highest point, the centripetal force is provided by the normal force acting on the point. Therefore, we can equate the centripetal acceleration to the expression involving the radius of curvature:
(2V)2ρ=4V2ρ
Hint: This equation relates the total velocity at the highest point to the radius of curvature.
Step 6: Relate Centripetal Acceleration to Normal Force
At the highest point, the centripetal force is equal to the normal force acting on the point. Thus, we can express the normal force as:
N=4V2ρ
Hint: The normal force acts as the centripetal force at the highest point.
Step 7: Solve for the Radius of Curvature
From the previous steps, we can derive the radius of curvature:
ρ=V2ac
Substituting Vtotal=2V:
ρ=(2V)2g=4V2g
Since the centripetal acceleration is also given by g at the highest point, we can conclude:
ρ=4R
Hint: The radius of curvature at the highest point is four times the radius of the wheel.
Final Result
The radius of curvature of the path of a point on the circumference of the wheel when it is at the highest point is:
ρ=4R
The wheel is rolling without sliding on a horizontal surface. This means that at the point of contact with the ground, the velocity is zero, and the wheel rotates about its center of mass.
At the highest point of the wheel, the point on the circumference has a velocity that is the sum of the translational velocity of the center of mass (V) and the tangential velocity due to rotation (rω). Since the wheel rolls uniformly, we have the relation V=rω.
At the highest point, the total velocity Vtotal can be expressed as:
Vtotal=V+rω=V+V=2V
The radius of curvature (ρ) is defined in terms of the centripetal acceleration. The centripetal acceleration ac for an object moving in a circular path is given by:
ac=V2totalρ
At the highest point, the centripetal force is provided by the normal force acting on the point. Therefore, we can equate the centripetal acceleration to the expression involving the radius of curvature:
(2V)2ρ=4V2ρ
At the highest point, the centripetal force is equal to the normal force acting on the point. Thus, we can express the normal force as:
N=4V2ρ
From the previous steps, we can derive the radius of curvature:
ρ=V2ac
Substituting Vtotal=2V:
ρ=(2V)2g=4V2g
ρ=4R
The radius of curvature of the path of a point on the circumference of the wheel when it is at the highest point is:
ρ=4R
Topper's Solved these Questions
Similar Questions
A wheel is rolling without sliding on a horizontal surface. Prove that velocities of all points on the circumference of the wheel are directed towards the top most point of the wheel.
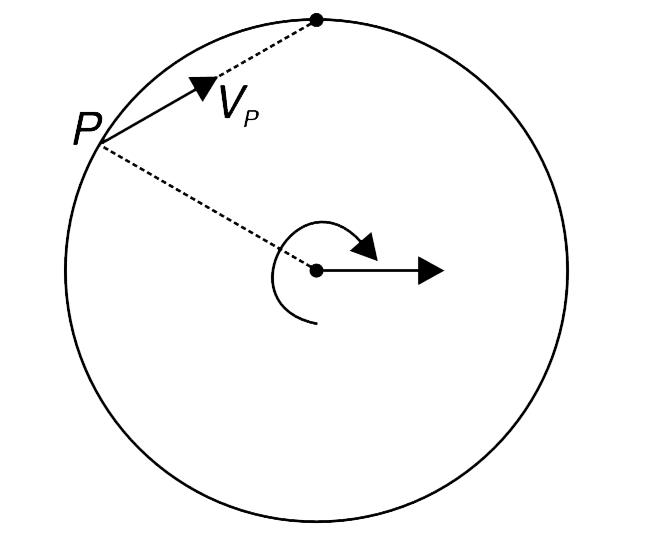
View SolutionA circular disc of radius r is rolling without slipping on a horizontal surface. What is the ratio of the translational KE and rotational KE of disc ?
View Solution
Knowledge Check
A ring of radius R rolls without slipping on a rough horizontal surface with a constant velocity. The radius of curvature of the path followed by any particle of the ring at the highest point of its path will be :
 .ARB2 RC4 RDnone of these
.ARB2 RC4 RDnone of theseA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.
 AVB2VC3VD2V3
AVB2VC3VD2V3A wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is
 A2√3m/sBzeroC3 m/sD√3m/s
A2√3m/sBzeroC3 m/sD√3m/s
A point A is located on the rim of a wheel of radius R which rolls witout slipping along a horizontal surface witih velocity V. Find the total distance traversed by the point A between successive moments at which it touches the surface.
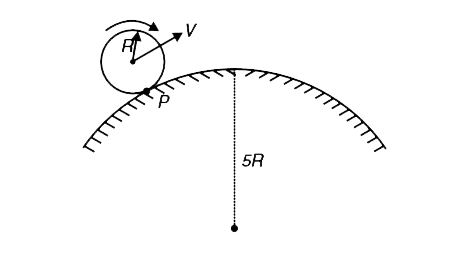
View SolutionA convex surface has a uniform radius of curvature equal to 5R. A wheel of radius R is rolling without sliding on it with a constant speed v. Find the acceleration of the point (P) of the wheel which is in contact with the convex surface.
View SolutionA wheel of radius R rolls without slipping on the horizontal surface with speed v0. When the contact point is P on the road, a small patch of mud separates from the wheel at its highest point strikes the road at point Q. Find distance PQ.
View SolutionA wheel of radius R rolls without slipping on a horizontal ground. The distance travelled by a point on the rim in one complete rotation is:
View SolutionA wheel of radius r rolls without slipping with a speed v on a horizontal road. When it is at a point A on the road, a small blob of mud separates from'the wheel at- its highest point and lands at point B on the road:
View Solution
