A metallic plate has been fabricated by welding two semicircular discs - D1 and D2 of radii R and R2 respectively (fig. a). O and O' are the centre of curvature of the two discs and each disc has a mass 6m. The plate is in xy plane. Now the plate is folded along the y axis so as to bring the part OAB in yz plane. (fig. b). The plate is now set free to be able to rotate freely about the z – axis. A particle of mass m, moving with a velocity v in the xy plane along the line x=d hits the plate and sticks to it (d<R) . Just before collision speed of the particle was v.
(a) 
(a) Find the moment of inertia of inertia of the plate about z axis.
(b) Find the angular speed of the plate after collision.
The correct Answer is:(a) 92mR2
(b) ω=2vd11R2
Topper's Solved these Questions
Similar Questions
Let →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .
View SolutionTwo particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time

View SolutionGiven a uniform disc of mass M and radius R . A small disc of radius R//2 is cut from this disc in such a way that the distance between the centres of the two discs is R//2 . Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View SolutionMoment of inertia of a thin semicircular disc (mass−M&radius=R) about an axis through point O and perpendicular to plane of disc, is given by :
 .
.
View SolutionCalculate the capacitance of a parallel plate capacitor having circular discs of radii 0.05m each. The separation between the discs is 1 mm .
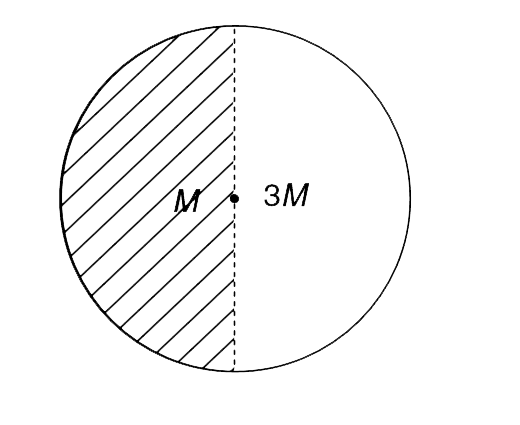
View SolutionTwo uniform semicircular discs, each of radius R, are stuck together to form a disc. Masses of the two semicircular parts are M and 3M. Find the moment of inertia of the circular disc about an axis perpendicular to its plane and passing through its centre of mass.
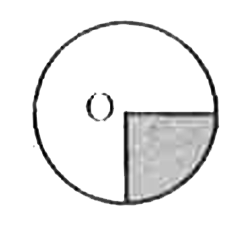
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionThe M.I. of a disc of mass M and radius R, about an axis passing through the centre O and perpendicular to the plane of the disc is MR22 . If one quarter of the disc is removed, the new moment of inertia of the disc will be
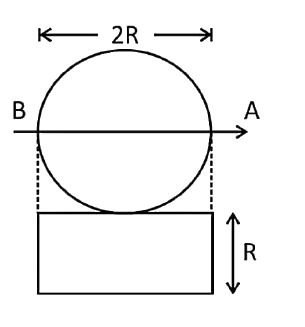
View SolutionA disc of mass m and radius R is attached to a rectangular plate of the same mass m, breadth R and length 2R as shown in figure. The moment of inertia of the system about the axis AB passing through the centre of the disc and along the plane is I=1α(313mR2).
View SolutionThe moment of Inertia of a uniform semicircular disc of mass M and radius 'r' about a line perpendicular to the plane of the disc through the centre is :
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionA capacitor is made of two circular plates of radius R each, separated by a distance d<<R. The capacitor is connected to a constant voltage. A thin conducting disc of radius r<<R and thickness t<<r is placed at a center of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m.
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionMoment of inertia of a thin semicircular disc (mass - M & radius = R) about an axis through point O and perpendicular to plane of disc, is given by : .
View SolutionGiven a uniform disc of mass M and radius R . A small disc of radius R//2 is cut from this disc in such a way that the distance between the centres of the two discs is R//2 . Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View Solution
