AB is a non uniform plank of length L=4R with its centre of mass at C such that AC=R. It is placed on a step with its one end A supported by a cylinder of radius R as shown in figure. The centre of mass of the plank is just outside the edge of the step. The cylinder is slowly rolled on the lower step such that there is no slipping at any of its contacts. Calculate the distance through which the centre of the cylinder moves before the plank loses contact with the horizontal surface of the upper step.

The correct Answer is:R
Topper's Solved these Questions
Similar Questions
A charge q is placed at the centre of a cylinder of radius R and length 2R. Then electric flux through the curved surface of the cylinder is
View Solution
Consider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll the plank always remains horizontal. there is no slipping at any point of contact. Calculate the acceleration of the cylinder and the frictional forces at the two contact.
View Solution
Knowledge Check
In the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
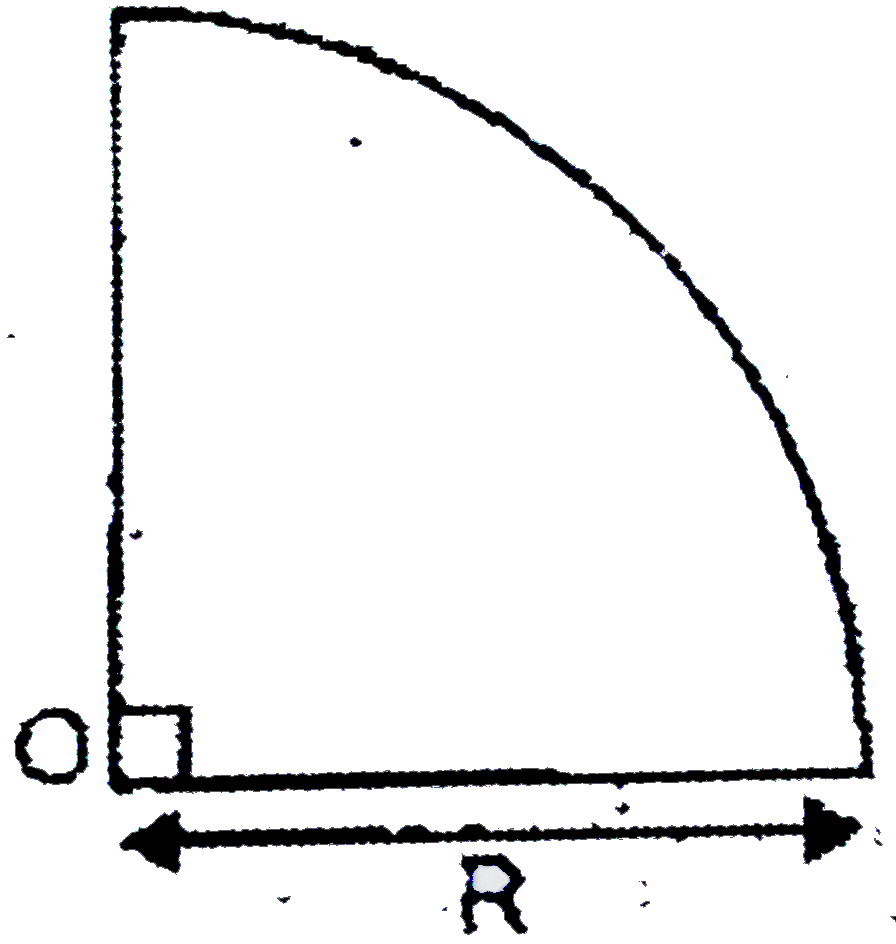 A4R3πB2r3πC√24R3πD√22R3π
A4R3πB2r3πC√24R3πD√22R3πa point charge q is placed at the centre of a cylinder of length L and radius R the electric flux through the curved surface of the cylinder is
Aqε0L√L2+R2Bqε0L√L2+2R2Cqε0L√L2+4R2Dq2ε0
A cylinder of radius R is to roll without slippoing between two planks as shown in the figure. ThenAangular velocity of the cylinder is vR counter clockwiseBangular velocity of the cylinder is 2vR clockwiseCvelocity of centre of mass of the cylinder is v towards leftDvelocity of centre of mass of the cylinder is 2v towards right.

Consider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll the plank always remains horizontal. there is no slipping at any point of contact. Calculate the acceleration of the cylinder and the frictional forces at the two contact.
View Solution
A cylinder of radius R is to roll without slipping between two planks as shown in the figure. Then
View SolutionA solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:

View Solution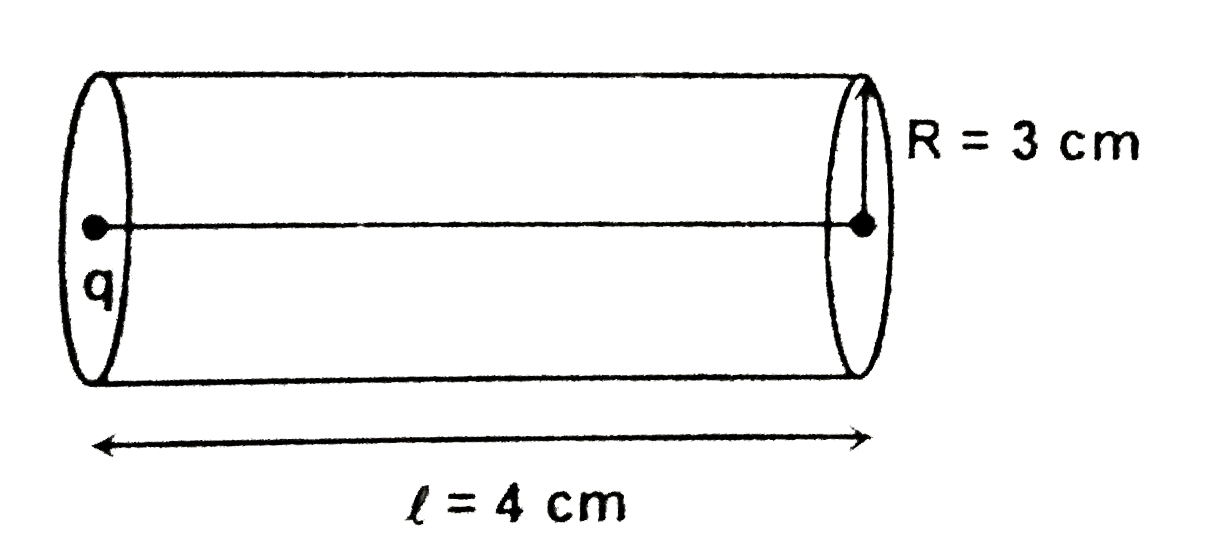
A point charge 'q' is placed at the centre of left circular end of a cylinder of length l=4cm and radius R=3 cm shown. Then the electric flux through the curved surface of the cylinder is
View Solution
A point charge 'q' is placed at the centre of left circular end of a cylinder of length l=4cm and radius R=3 cm shown. Then the electric flux through the curved surface of the cylinder is
View Solution
